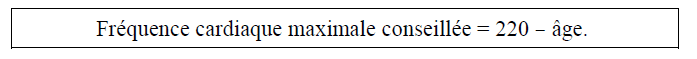Le sujet du brevet de maths 2017 à Pondichéry.
L’épreuve a eu lieu le mardi 2 mai 2017 à Pondichéry en Inde.
DIPLÔME NATIONAL DU BREVET
SESSION 2017
PREMIÈRE ÉPREUVE
1ère partie
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 heures – 50 points
(dont 5 points pour la présentation de la copie et l’utilisation de la langue française)
Le sujet est constitué de sept exercices indépendants.
Le candidat peut les traiter dans l’ordre qui lui convient.
Toutes les réponses doivent être justifiées, sauf si une indication contraire est donnée.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la recherche. Elle sera prise en compte dans la notation.
THÉMATIQUE COMMUNE DE L’ÉPREUVE DE MATHÉMATIQUES-SCIENCES : L’ÉNERGIE
Exercice 1 (5 points)
On considère l’expression .
1. Développer E.
2. Factoriser E et vérifier que E=2F, où .
3. Déterminer tous les nombres x tels que .
Exercice 2 (6 points)
Un sac contient 20 boules ayant chacune la même probabilité d’être tirée.
Ces 20 boules sont numérotées de 1 à 20. On tire une boule au hasard dans le sac.
Tous les résultats seront donnés sous forme de fractions irréductibles.
1. Quelle est la probabilité de tirer la boule numérotée 13 ?
2. Quelle est la probabilité de tirer une boule portant un numéro pair ?
3. A-t-on plus de chances d’obtenir une boule portant un numéro multiple de 4 que d’obtenir une boule portant un numéro diviseur de 4 ?
4. Quelle est la probabilité de tirer une boule portant un numéro qui soit un nombre premier ?
Exercice 3 (7 points)
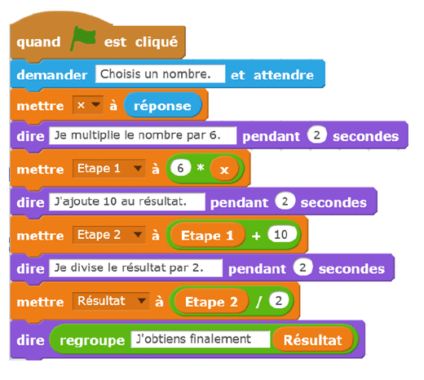
On considère le programme de calcul ci-dessous dans lequel x, Etape 1,
Etape 2 et Résultat sont quatre variables.
1. a. Julie a fait fonctionner ce programme en choisissant le nombre 5.
Vérifier que ce qui est dit à la fin est : « J’obtiens finalement 20 ».
b. Que dit le programme si Julie le fait fonctionner en choisissant au départ le nombre 7 ?
2. Julie fait fonctionner le programme, et ce qui est dit à la fin est : « J’obtiens finalement 8 ».
Quel nombre Julie a-t-elle choisi au départ ?
3. Si l’on appelle le nombre choisi au départ, écrire en fonction de l’expression obtenue à la fin du
programme, puis réduire cette expression autant que possible.
4. Maxime utilise le programme de calcul ci-dessous:
Peut-on choisir un nombre pour lequel le résultat obtenu par Maxime est le même que celui obtenu par Julie ?
Exercice 4 (7 points)
Pour ses 32 ans, Denis a acheté un vélo d’appartement afin de pouvoir s’entraîner pendant l’hiver.
La fréquence cardiaque (FC) est le nombre de pulsations (ou battements) du coeur par minute.
1. Denis veut estimer sa fréquence cardiaque : en quinze secondes, il a compté 18 pulsations. A quelle fréquence cardiaque, exprimée en pulsations par minute, cela correspond-il ?
2. Son vélo est équipé d’un cardiofréquencemètre qui lui permet d’optimiser son effort en enregistrant, dans ce cardiofréquencemètre, toutes les pulsations de son coeur. À un moment donné, le cardiofréquencemètre a mesuré un intervalle de 0,8 seconde entre deux pulsations. Calculer la fréquence cardiaque qui sera affichée par le cardiofréquencemètre.
3. Après une séance d’entraînement, le cardiofréquencemètre lui a fourni les renseignements suivants :

a. Quelle est l’étendue des fréquences cardiaques enregistrées ?
b. Denis n’a pas chronométré la durée de son entraînement. Quelle a été cette durée ?
4. Denis souhaite connaître sa fréquence cardiaque maximale conseillée (FCMC) afin de ne pas la dépasser et ainsi de ménager son coeur. La FCMC d’un individu dépend de son âge , exprimé en années, elle peut s’obtenir grâce à la formule suivante établie par Astrand et Ryhming :
On note f (a) la FCMC en fonction de l’âge , on a donc f(a)=220−a .
a. Vérifier que la FCMC de Denis est égale à 188 pulsations/minute.
b. Comparer la FCMC de Denis avec la FCMC d’une personne de 15 ans.
5. Après quelques recherches, Denis trouve une autre formule permettant d’obtenir sa FCMC de façon plus précise. Si désigne l’âge d’un individu, sa FCMC peut être calculée à l’aide de la formule de Gellish :
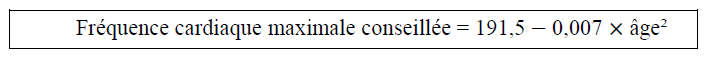
On note g(a) la FCMC en fonction de l’âge , on a donc
Denis utilise un tableur pour comparer les résultats obtenus à l’aide des deux formules :
Quelle formule faut-il insérer dans la cellule C2 puis recopier vers le bas, pour pouvoir compléter la colonne « FCMC g(a) (Gellish) » ?
Exercice 5 (8 points)
Un TeraWattheure est noté : 1 TWh.
La géothermie permet la production d’énergie électrique grâce à la chaleur des nappes d’eau souterraines.
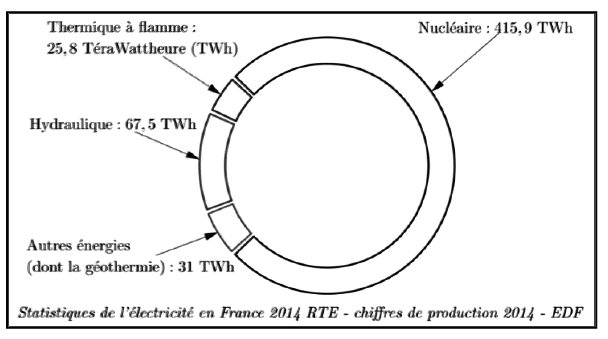
Le graphique ci-dessous représente les productions d’électricité par différentes sources d’énergie en
France en 2014.
1. a. Calculer la production totale d’électricité en France en 2014.
b. Montrer que la proportion d’électricité produite par les « Autres énergies (dont la géothermie) » est environ égale à 5,7 %.
2. Le tableau suivant présente les productions d’électricité par les différentes sources d’énergie, en France, en 2013 et en 2014.

Alice et Tom ont discuté pour savoir quelle est la source d’énergie qui a le plus augmenté sa production d’électricité. Tom pense qu’il s’agit des « Autres énergies (dont la géothermie) » et Alice pense qu’il s’agit du « Nucléaire ». Quel est le raisonnement tenu par chacun d’entre eux ?
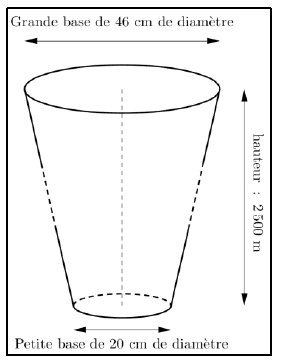
3. La centrale géothermique de Rittershoffen (Bas Rhin) a été inaugurée le 7 juin 2016. On y a creusé un
puits pour capter de l’eau chaude sous pression, à 2500 m de profondeur, à une température de 170 degrés Celsius.
Ce puits a la forme du tronc de cône représenté ci-contre.
Les proportions ne sont pas respectées.
On calcule le volume d’un tronc de cône grâce à la formule suivante :
où h désigne la hauteur du tronc de cône, R le rayon de la grande base et r le
rayon de la petite base.
a. Vérifier que le volume du puits est environ égal à 225 .
b. La terre est tassée quand elle est dans le sol. Quand on l’extrait, elle n’est
plus tassée et son volume augmente de 30%.
Calculer le volume final de terre à stocker après le forage du puits.
Exercice 6 (7 points)
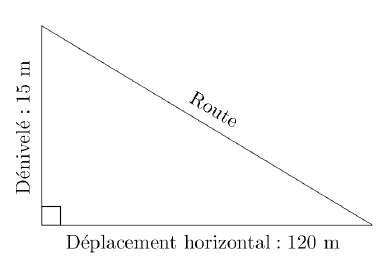
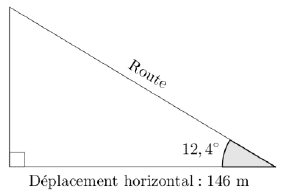
On obtient la pente d’une route en calculant le quotient du dénivelé (c’est-à-dire du déplacement vertical) par le déplacement horizontal correspondant. Une pente s’exprime sous forme d’un pourcentage.
Sur l’exemple ci-dessous, la pente de la route est :
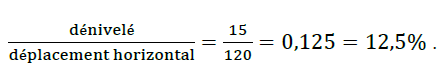
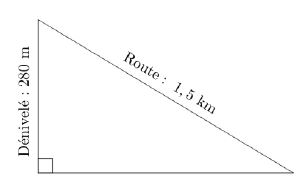
Classer les pentes suivantes dans l’ordre décroissant,
c’est-à-dire de la pente la plus forte à la pente la moins forte.
Route descendant du château des Adhémar,à Montélimar.
Tronçon d’une route descendant du col du Grand Colombier (Ain).
Tronçon d’une route descendant de l’Alto de l’Angliru (région des Asturies, Espagne).
Exercice 7 (5 points)
Alban souhaite proposer sa candidature pour un emploi dans une entreprise. Il doit envoyer dans une seule enveloppe : 2 copies de sa lettre de motivation et 2 copies de son Curriculum Vitæ (CV). Chaque copie est rédigée sur une feuille au format A4.
1. Il souhaite faire partir son courrier en lettre prioritaire. Pour déterminer le prix du timbre, il obtient sur internet la grille de tarif d’affranchissement suivante :

Le tarif d’affranchissement est-il proportionnel à la masse d’une lettre ?
2. Afin de choisir le bon tarif d’affranchissement, il réunit les informations suivantes :
- Masse de son paquet de 50 enveloppes : 175 g.
- Dimensions d’une feuille A4 : 21 cm de largeur et 29,7 cm de longueur.
- Grammage d’une feuille A4 : 80
(le grammage est la masse par m² de feuille).
- 1 m² = 104 cm².
Quel tarif d’affranchissement doit-il choisir ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet Pondichéry 2017 : Sujet de Maths – Brevet des Collèges» au format PDF.
D'autres cours et exercices à consulter
- Polynésie Française : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2022 en France : sujet et corrigé du brevet
- Brevet de maths 2023 avec le sujet blanc et son corrigé
- Sujet du brevet de maths France 2016
- Brevet Maths 2021 – Asie Pacifique – Sujet et corrigé en PDF
- France : Brevet de maths 2024 avec sujet et corrigé en PDF
- Brevet Asie Pacifique 2016 : sujet et corrigé en PDF.
- Brevet de maths 2023 : sujet pour réviser le brevet en ligne.