DIPLÔME NATIONAL DU BREVET
SESSION 2017
PREMIÈRE ÉPREUVE
1ère partie
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 heures – 50 points
Thématique commune du sujet de Mathématiques, Physique-Chimie et Sciences de la Vie et de la Terre
Le Sport
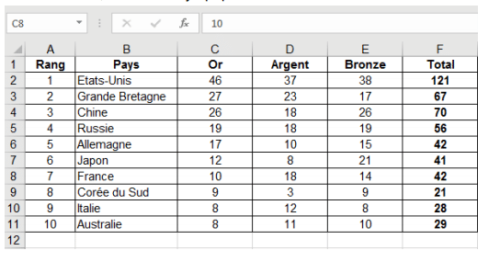
Exercice 1 : (9 points)
Sur une feuille de calcul, on a reporté le classement des dix premiers pays, par le
nombre de médailles, aux Jeux Olympiques de Rio en 2016.
1. Quelle formule, parmi les trois proposées, a été saisie dans la cellule F2 de
cette feuille de calcul, avant qu’elle soit étirée vers le bas ?

2. On observe la série des nombres de médailles d’or de ces dix pays.
a. Quelle est l’étendue de cette série ?
b. Quelle est la moyenne de cette série ?
3. Quel est le pourcentage de médailles d’or remportées par la France par rapport
à son nombre total de médailles ? Arrondir le résultat au dixième de %.
4. Le classement aux Jeux Olympiques s’établit selon le nombre de médailles d’or
obtenues et non selon le nombre total de médailles. Pour cette raison, la France
avec 42 médailles se retrouve derrière le Japon qui n’en a que 41. En observant
l’Italie et l’Australie, établir la règle de classement en cas d’égalité sur le nombre
de médailles d’or.
5. Un journaliste sportif propose une nouvelle procédure pour classer les pays :
chaque médaille d’or rapporte 3 points, chaque médaille d’argent rapporte 2
points et chaque médaille de bronze rapporte 1 point. Dans ces conditions, la
France dépasserait-elle le Japon ?
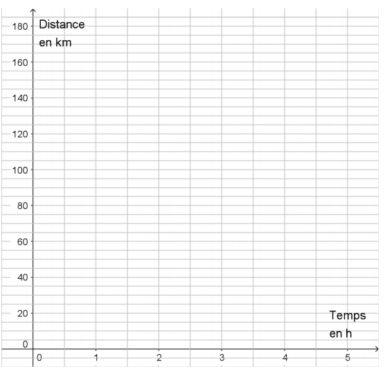
Exercice 2 : (10 points)
Le 17 juillet 2016, une spectatrice regarde l’étape « Bourg-enBresse / Culoz » du Tour de France.

distance parcourue par celui-ci au bout de 1 h de course.
Elle obtient le tableau suivant :
1. Quelle distance a-t-il parcourue au bout de 2 h 30 min de course ?
2. Montrer qu’il a parcouru 30 km lors de la troisième heure de course.
3. A-t-il été plus rapide lors de la troisième ou bien lors de la quatrième heure de
course ?
4. Répondre aux questions qui suivent sur la feuille ANNEXE page 7 sur 7, qui est
à rendre avec la copie.
a. Placer les 9 points du tableau dans le repère. On ne peut pas placer le
point d’abscisse 1 puisque l’on ne connaît pas son ordonnée.
b. En utilisant votre règle, relier les points consécutifs entre eux.
5. En considérant que la vitesse du cycliste est constante entre deux relevés,
déterminer, par lecture graphique, le temps qu’il a mis pour parcourir 75 km.
6. On considère que la vitesse du cycliste est constante entre le premier relevé
effectué au bout de 0,5 h de course et le relevé effectué au bout de 1,5 h de
course ; déterminer par lecture graphique la distance parcourue au bout de 1 h
de course.
7. Soit la fonction, qui au temps de parcours du cycliste Thomas VOECKLER,
associe la distance parcourue. La fonction est-elle linéaire ?
Exercice 3 : (6 points)
Le jardinier d’un club de football décide de semer à nouveau du gazon sur l’aire de
jeu. Pour que celui-ci pousse correctement, il installe un système d’arrosage
automatique qui se déclenche le matin et le soir, à chaque fois, pendant 15 minutes.
– Le système d’arrosage est constitué de 12 circuits indépendants.
– Chaque circuit est composé de 4 arroseurs.
– Chaque arroseur a un débit de 0,4 m3 d’eau par heure.
Combien de litres d’eau auront été consommés si on arrose le gazon pendant tout le
mois de juillet ?
On rappelle que 1 m3 = 1 000 litres et que le mois de juillet compte 31 jours.
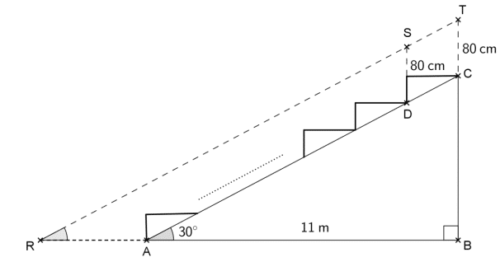
Exercice 4 : (7 points)
La figure ci-dessous représente le plan de coupe d’une tribune d’un gymnase. Pour
voir le déroulement du jeu, un spectateur du dernier rang assis en C doit regarder audessus
du spectateur placé devant lui et assis en D. Une partie du terrain devant la
tribune lui est alors masquée. On considèrera que la hauteur moyenne d’un spectateur
assis est de 80 cm (CT = DS = 80 cm).
Sur ce plan de coupe de la tribune :
– les points R, A et B sont alignés horizontalement et les points B, C et T sont
alignés verticalement ;
– les points R, S et T sont alignés parallèlement à l’inclinaison (AC) de la tribune ;
– on considérera que la zone représentée par le segment [RA] n’est pas visible
par le spectateur du dernier rang ;
– la largeur au sol AB de la tribune est de 11 m et l’angle d’inclinaison de la
tribune mesure 30°.
1. Montrer que la hauteur BC de la tribune mesure 6,35 m, arrondie au centième
de mètre près.
2. Quelle est la mesure de l’angle ?
3. Calculer la longueur RA en centimètres. Arrondir le résultat au centimètre près.
Exercice 5 : (7 points)
L’épreuve du marathon consiste à parcourir le plus rapidement possible la distance de
42,195 km en course à pied. Cette distance se réfère historiquement à l’exploit effectué
par le Grec PHILLIPIDÈS, en 490 av. J-C, pour annoncer la victoire des Grecs contre
les Perses. Il s’agit de la distance entre Marathon et Athènes.
1. En 2014, le kényan Dennis KIMETTO a battu l’ancien record du monde en
parcourant cette distance en 2 h 2 min 57 s. Quel est alors l’ordre de grandeur
de sa vitesse moyenne : 5 km/h, 10 km/h ou 20 km/h ?
2. Lors de cette même course, le britannique Scott OVERALL a mis 2 h 15 min
pour réaliser son marathon. Calculer sa vitesse moyenne en km/h. Arrondir la
valeur obtenue au centième de km/h.
3. Dans cette question, on considérera que Scott OVERALL court à une vitesse
constante. Au moment où Dennis KIMETTO franchit la ligne d’arrivée,déterminer :
a. le temps qu’il reste à courir à Scott OVERALL ;
b. la distance qu’il lui reste à parcourir. Arrondir le résultat au mètre près.
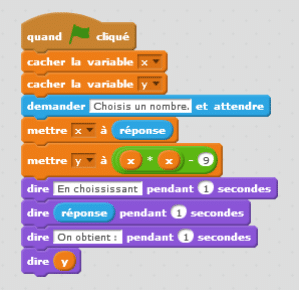
Exercice 6 : (6 points)
La figure ci-dessous est la copie d’écran d’un programme réalisé avec le logiciel « Scratch ».
1. Montrer que si on choisit 2 comme nombre de départ, alors le programme renvoie −5
2. Que renvoie le programme si on choisit au départ :
a. le nombre 5 ?
b. le nombre −4 ?
3. Déterminer les nombres qu’il faut choisir au départ pour que le programme renvoie 0.
ANNEXE
À détacher du sujet et à joindre avec la copie.
Exercice 2 question 4
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2017 – sujet et corrigé du rattrapage en Polynésie» au format PDF.
D'autres cours et exercices à consulter
- Brevet de maths 2017 : sujet blanc pour réviser en ligne.
- Brevet de maths 2017 sujet 0
- Brevet de maths 2022 : sujet et corrigé du brevet en PDF
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet de maths 2021 : sujet blanc n° 3 en PDF
- Sujet 2018 France du brevet de maths des collèges
- Brevet de maths en France 2019 : sujet et corrigé à télécharger en PDF
- Brevet de maths 2016 : sujet blanc pour réviser en PDF.