Annales du bac de maths 2025 avec des extraits du baccalauréat.
De nombreux exercices type du bac de maths 2024 classés par chapitres.
Ces exercices type vous permettent de réviser le baccalauréat des lycées afin de vous préparer dans les meilleurs conditions.
En complément de tous les sujets du baccalauréat de mathématiques des sessions antérieures, Mathovore met à votre disposition des extraits de sujet qui ciblent chaque chapitre du programme de terminale.
Les fonctions numériques
On considère l’application f de dans
définie par :
si ;
et pour tout de
.
1. Etudier la restriction de f à l’intervalle [0;2] et construire la courbe représentative de
.
Comment peut-on en déduire la courbe représentative de la restriction de f à l’intervalle [2n;2n+2] où n est élément de .
2. Démontrer que :
Si
3. Est-ce que f est continue sur ?
4. Est-ce que f est dérivable sur ?
Les suites numériques
Soient et
les suites définies pour tout entier naturel n par :
1.a. Montrer que est une suite géométrique à termes positifs .
b. Calculer la somme en fonction de n et en déduire la somme
en fonction de n .
c. déterminer et
.
2. On définit la suite par
pour tout entier n .
Montrer que la suite est une suite arithmétique .
Calculer en fonction de n et déterminer
3. Calculer le produit en fonction de n.
En déduire .
Probabilités :
Un joueur débute un jeu au cours duquel est amené à faire successivement plusieurs parties.
La probabilité que le joueur perde la première partie est de 0,2.
Le jeu se déroule ensuite de la manière suivante :
S’il gagne une partie, alors il perd la suivante avec une probabilité de 0,05 ;
S’il perd une partie, alors il perd la suivante avec une probabilité de 0,1.
1) On appelle :
E1 l’événement « le joueur perd la première partie » ;
E2 l’événement « le joueur perd la deuxième partie » ;
E3 l’événement « le joueur perd la troisième partie ».
On appelle X la variable aléatoire qui donne le nombre de fois où le joueur perd lors des trois premières parties.
On pourra s’aider d’un arbre pondéré.
a) Quelles sont les valeurs prises par X ?
b) Montrer que la probabilité de l’événement (X = 2) est égale à 0,031 et que celle de l’événement (X = 3) est égale à 0,002.
c) Déterminer la loi de probabilité de X.
d) Calculer l’espérance de X.
2) Pour tout entier naturel n non nul, on note En l’événement : « le joueur perd la n-ième partie », l’événement contraire, et on note pn la probabilité de l’événement En.
a) Exprimer pour tout entier naturel n non nul, les probabilités des événements
et
en fonction de pn.
b) En déduire que pn+1 = 0,05 pn + 0,05 pour tout entier naturel n non nul.
3) On considère la suite (un) définie pour tout entier naturel n non nul par .
a) Montrer que (un) est une suite géométrique dont on précisera la raison et le premier terme.
b) En déduire, pour tout entier naturel n non nul, un puis pn en fonction de n.
c) Calculer la limite de pn quand n tend vers.
Les nombres complexes
Rechercher tous les couples de nombres complexes satisfaisant aux conditions :
.
Donner la forme trigonométrique de chacun des nombres ainsi obtenus .
Les nombres complexes et la trigonométrie
Soient les nombres complexes et
.
1. Mettre sous forme trigonométrique .
En déduire que :
et
.
3. On considere l’équation d’inconnue réelle x :
a. Résoudre cette équation dans .
b. Placer les points images des solutions sur le cercle trigonométrique .
Les équations différentielles
On considère l’équation différentielle .
1. Démontrer que la fonction u définie sur par
est une solution de (E) .
2. Résoudre l’équation différentielle .
3. Démontrer qu’une fonction v définie sur est solution de (E) si et seulement si v-u est solution de
.
4. En déduire toutes les solutions de l’équation (E) .
5. Déterminer la fonction, solution de (E), qui prend la valeur 1 en 0 .
6. Le plan est muni d’un repère orthonormé
Soit la fonction f définie sur par
.
On note C la courbe représentative de f dans le repère
a. Etudier les variations de f puis dresser son tableau de variation .
b. Tracer C .
Le barycentre de points pondérés
On considère un triangle ABC du plan .
1.a. Déterminer et construire le point G, barycentre du système de points pondérés :
.
b. Déterminer et construire le point G’, barycentre du système de points pondérés :
.
2.a. Soit J le milieu de [AB].
Exprimer et
en fonction de
et
et en déduire l’intersection des droites (GG’) et (AB) .
b. Montrer que le barycentre I du système de points pondérés :
appartient à (GG’) .
3. Soit D un point quelconque du plan et O le milieu de [CD] et K le milieu de [OA] .
a. Déterminer trois réels a, b, c tels que K soit le barycentre du système de points pondérés :
.
b. Soit X le point d’intersection de (DK) et (AC).
Déterminer les réels a’ et c’ tels que X soit barycentre du système de points pondérés :
.
La géométrie dans l’espace
On se propose d’étudier une modélisation d’une tour de contrôle de trafic aérien, chargée de surveiller deux routes aériennes représentées par deux droites de l’espace .
L’espace est rapporté à un repère orthonormal d’unité 1 km .
Le plan représente le sol .
les deux routes aériennes à contrôler sont représentées par deux droites et
, dont on connait des représentations paramétriques :
1.a. Indiquer les coordonnées d’un vecteur directeur de la droite
et d’un vecteur
directeur de la droite
.
b. Prouver que les droites et
ne sont pas coplanaires .
2. On veut installer au sommet S de la tour de contrôle, de coordonnées S(3;4;0,1), n appareil de surveillance qui émet un rayon représenté par une droite notée (R).
Soit le plan contenant S et
et soit
le plan contenant S et
.
a. Montre que est sécante à
.
b. Montre que est sécante à
.
c. Un technicien affirme qu’il est possible de choisir la direction de (R) pour que cette droite coupe chacune des droites et
.
Cette affirmation est-elle vraie? (justifier la réponse)
Problème sur les équations différentielles
Partie A
On donne un entier naturel n strictement positif, et on considère l’équation différentielle :
1. On fait l’hypothèse que deux fonctions g et h, définies et dérivables sur , vérifient, pour tout x réel :
a. Montrer que g est solution de si et seulement si, pour tout x réel :
.
b. En déduire la fonction h associée à une solution g de , sachant que f(0)=0.
Quelle est alors la fonction g?
2. Soit une fonction dérivable sur
.
a. Montrer que est solution de
si et seulement si
est solution de l’équation :
(F) y’+y=0
b. Résoudre (F) .
c. déterminer la solution générale de l’équation
.
d. Déterminer la solution f de l’équation vérifiant f(0)=0 .
Partie B
Le but de cette partie est de montrer que :
1. On pose, pour tout x réel,
.
a. vérifier que est solution de l’équation différentielle : y’+y=
.
b. Pour tout entier strictement positif n, on définit la fonction comme la solution de l’équation différentielle y’+y=
vérifiant
.
En utilisant la partie A, montrer par récurrence que , pour tout x réel et tout entier :
.
2. Pour tout entier naturel n, on pose :
a. Montrer, pour tout entier naturel n et pour tout x élément de l’intervalle [0;1], l’encadrement :
.
En déduire que , puis déterminer la limite de la suite
.
b. Montrer, pour tout entier naturel k non nul, l’égalité :
.
c. Calculer et déduire de ce qui précède que :
.
d. En déduire finalement :
Les similitudes planes et enseignement de spécialité
Le plan complexe P est rapporté à un repère orthonormé .
On désigne par s l’application qui à tout point M de P de coordonnées (x,y) associe le point M’ de coordonnées (x’, y’) tel que :
1. Déterminer l’affixe z’ de M’ en fonction de l’affixe z de M .
2. Démontrer que s est une similitude plane directe.
Préciser son angle, son rapport et son centre I .
3. Soit g l’application qui à tout point M de P associe l’isobarycentre G des points M,M’=s(M) et M »=s(M’) .
a. Calculer , en fonction de l’affixe z de M, les affixes des points M » et G.
b. Démontrer que g est une similitude plane directe.
Quel est son centre ?
c. Déterminer l’affixe du point Mo tel que g(Mo) soit le point O .
Reporter sur une figure les points Mo, M’o, M »o correspondants, ainsi que le point I, centre de la similitude s .
Extraits du baccalauréat S sur l’arithmétique
Soit n un entier naturel .
1. trouver suivant les valeurs de n, les restes de la division de par 13 .
2. En déduire que est divisible par 13.
3. Démontrer que, pour tout entier naturel n supérieur ou égal à 1, le nombre est divisible par 13 .
Les similitudes planes en spécialité
Dans le plan orienté, on considère un carré direct ABCD de centre O.
Soit P un point du segment [BC] distinct de B .
On note Q l’intersection de (AP) avec (CD) .
La perpendiculaire à (AP) passant par A coupe (BC) en R et (CD) en S .
1. Faire une figure .
2. Soit r la rotation de centre A et d’angle .
a. Préciser, en justifiant votre réponse, l’image de la droite (BC) par la rotation r .
b. Déterminer les images de R et de P par r .
c. Quelle est la nature de chacun des triangles ARQ et APS ?
3. On note N le milieu du segment [PS] et M celui du segment [QR] .
Soit s la similitude de centre A, d’angle et de rapport
.
a. Déterminer les images respectives de R et de P par s .
b. Quel est le lieu géométrique du point N quand P décrit le segment [BC] privé de B ?
c. Démontrer que les points M, B, N et D sont alignés .
Exponentielle au bac S en Amérique du Nord
L’objet de cette question est de démontrer que .
On supposera connus les résultats suivants :
· La fonction exponentielle est dérivable sur R et est égale à sa fonction dérivée ;
· ;
· pour tout réel x, on a ;
· soient deux fonctions et
définies sur l’intervalle
où A est un réel positif.
Si pour tout x de ,
et si
alors
.
a) on considère la fonction g définie sur par
.
Montrer que pour tout x de ,
.
b) En déduire que .
Similitudes au bac S à Pondichéry en spécialité
Le plan complexe est rapporté a un repère orthonormal direct .
On considère l’application qui au point M d’affixe z fait correspondre le point M’ d’affixe
tel que :
.
- On note x et x ‘, y et y ‘ les parties réelles et les parties imaginaires de z et z ‘ .
Démontrer que et
2. a. Déterminer l’ensemble des points invariants par f.
b. Quelle est la nature de l’application f ?
3. Déterminer l’ensemble D des points M d’affixe z tels que z ‘ soit réel.
4. On cherche à déterminer les points de D dont les coordonnées sont entières.
Donner une solution particulière (x0, y0) appartenant a Z2 de l’équation 4x – 3y = 2.
Déterminer l’ensemble des solutions appartenant à Z2 de l’équation 4x – 3y = 2.
5. On considère les points M d’affixe z = x + iy tels que x= 1 et . Le point M’ = f(M) a pour affixe z ‘ .
Déterminer les entiers y tels que Re(z ‘ ) et lm(z ‘ ’) soient entiers (on pourra utiliser les congruences modulo 5).
Géométrie dans l’espace au bac S en France :
Soient un réel strictement positif et OABC un tétraèdre tel que :
– OAB, OAC et OBC sont des triangles rectangles en O,
– OA = OB = OC = .
On appelle I le pied de la hauteur issue de C du triangle ABC, H le pied de la hauteur issue de O du triangle OIC, et D le point de l’espace défini par :
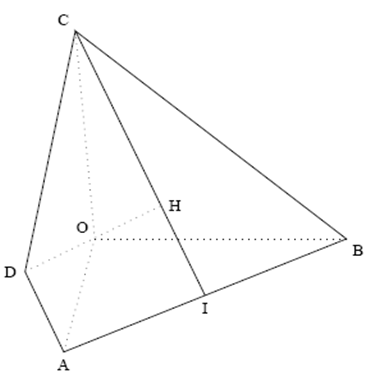
1. Quelle est la nature du triangle ABC ?
2. Démontrer que les droites (OH) et (AB) sont orthogonales, puis que H est l’orthocentre du triangle ABC.
3. Calcul de OH
a. Calculer le volume V du tétraèdre OABC puis l’aire S du triangle ABC.
b. Exprimer OH en fonction de V et de S, en déduire que .
4. Étude du tétraèdre ABCD.
L’espace est rapporté au repère orthonormal .
(a) Démontrer que le point H a pour coordonnées : .
(b) Démontrer que le tétraèdre ABCD est régulier (c’est-à-dire que toutes ses arêtes ont même longueur).
(c) Soit le centre de la sphère circonscrite au tétraèdre ABCD.
Démontrer que est un point de la droite (OH) puis calculer ses coordonnées.
Bactéries et équations différentielles
Soit le nombre de bactéries introduites dans un milieu de culture à l’instant
(
étant un réel strictement positif, exprimé en millions d’individus).
Ce problème a pour objet l’étude de deux modèles d’évolution de cette population de bactéries :
– un premier modèle pour les instants qui suivent l’ensemencement (partie A),
– un second modèle pouvant s’appliquer sur une longue période (partie B).
Partie A
Dans les instants qui suivent l’ensemencement du milieu de culture,
on considère que la vitesse d’accroissement des bactéries est proportionnelle au nombre de bactéries en présence.
Dans ce premier modèle, on note le nombre de bactéries à l’instant
(exprimé en millions d’individus).
La fonction est donc solution de l’équation différentielle :
. (où
est un réel strictement positif dépendant des conditions expérimentales).
1. Résoudre cette équation différentielle, sachant que .
2. On note le temps de doublement de la population bactérienne.
Démontrer que, pour tout réel t positif : .
Partie B
Le milieu étant limité (en volume, en éléments nutritifs, …), le nombre de bactéries ne peut pas croître indéfiniment de façon exponentielle. Le modèle précédent ne peut donc s’appliquer sur une longue période.
Pour tenir compte de ces observations, on représente l’évolution de la population de bactéries de la façon suivante :
Soit est le nombre de bactéries à l’instant t (exprimé en millions d’individus) ;
la fonction est une fonction strictement positive et dérivable sur
qui vérifie pour tout
de
la relation :
où M est une constante strictement positive dépendant des conditions expérimentales et le réel défini dans la partie A.1. (a) Démontrer que si
est une fonction strictement positive vérifiant la relation (E),
alors la fonction est solution de l’équation différentielle
(b) Résoudre (E ’ ).
(c) Démontrer que si est une solution strictement positive de (E ’ ), alors
vérifie (E).
2. On suppose désormais que, pour tout réel positif
où est une constante strictement supérieure à 1 dépendant des conditions expérimentales.
(a) Déterminer la limite de en
et démontrer, pour tout réel
positif ou nul, la double inégalité :
.
(b) Étudier le sens de variation de (on pourra utiliser la relation (E)).
Démontrer qu’il existe un réel unique positif tel que
.
(c) Démontrer que .
Étudier le signe de .
En déduire que la vitesse d’accroissement du nombre de bactéries est décroissante à partir de l’instant défini ci-dessus.
Exprimer en fonction de
et
.
(d) Sachant que le nombre de bactéries à l’instant est
, calculer le nombre moyen de bactéries entre les instants 0 et
, en fonction de M et
.
Probabilités au bac S en Nouvelle Calédonie :
Un jeu consiste à tirer simultanément trois boules d’une urne contenant six boules blanches et quatre boules rouges.
On suppose que tous les tirages sont équiprobables.
Si les trois boules tirées sont rouges, le joueur gagne 100 € ;
si exactement deux boules tirées sont rouges, il gagne 15 €
et si une seule est rouge il gagne 4 €.
Dans tous les autre cas, il ne gagne rien.
Soit X la variable aléatoire qui prend pour valeurs le gain en euros du joueur lors d’un jeu.
1°) Déterminer la loi de probabilité de la variable aléatoire X.
2°) Pour un jeu, la mise est de 10 €. Le jeu est-il favorable au joueur, c’est-à-dire l’espérance mathématiques est-elle strictement supérieure à 10 ?
3°) Pour l’organisateur, le jeu ne s’avérant pas suffisamment rentable, celui-ci envisage deux solutions:
_ soit augmenter la mise de 1 €, donc passer à 11 €,
_ soit diminuer chaque gain de 1 €, c’est-à-dire ne gagner que 99 €, 14 e ou 3€.
Quelle est la solution la plus rentable pour l’organisateur ?
Arithmétique en spécialité
On considère deux entiers naturels, non nuls, x et y premiers entre eux.
On pose S= x + y et P = xy.
1°) a) Démontrer que x et S sont premiers entre eux, de même que y et S.
b) En déduire que S = x+y et P =xy sont premiers entre eux.
c) Démontrer que les nombres S et P sont de parités différentes ( l’un pair, l’autre impair).
2°) Déterminer les diviseurs positifs de 84 et les ranger par ordre croissant.
3°) Trouver les nombres premiers entre eux x et y tels que : SP = 84.
4°) Déterminer les deux entiers naturels a et b vérifiant les conditions suivantes:
avec d = pgcd(a;b)
(On pourra poser a = dx et b = dy avec x et y premiers entre eux).
Nombres complexes
1°) On considère le polynôme P de la variable complexe z, défini par:
.
a) Déterminer le nombre réel y tel que iy soit solution de l’équation P(z) = 0.
b) Trouver deux nombres réels a et b tels que, pour tout nombre complexe z,
on ait
c) Résoudre dans l’ensemble des nombres complexes, l’équation P(z) = 0.
2°) Le plan complexe est rapporté à un repère orthonormal direct .
On prendra 1 cm pour unité graphique.
a) Placer les points A, B et I d’affixes respectives zA = -7 + 5 i ; zB = -7 – 5 i et .
b) Déterminer l’affixe de l’image du point I par la rotation de centre O et d’angle .
c) Placer le point C d’affixe zC = 1 + i. Déterminer l’affixe du point N tel que ABCN soit un parallélogramme.
d) Placer le point D d’affixe zA = 1 + 11 i.
Calculer sous forme algébrique puis sous forme trigonométrique.
Justifier que les droites (AC) et (BD) sont perpendiculaires et en déduire la nature du quadrilatère ABCD.
Probabilités
Une salle informatique d’un établissement scolaire est équipée de 25 ordinateurs dont 3 sont défectueux.
Tous les ordinateurs ont la même probabilité d’être choisis.
On choisit au hasard deux ordinateurs de cette salle.
Quelle est la probabilité que ces deux ordinateurs soient défectueux ?
La durée de vie d’un ordinateur (c’est-à-dire la durée de fonctionnement avant la première panne), est une variable aléatoire X qui suit une loi exponentielle de paramètre λ avec λ > 0.
Ainsi, pour tout réel t positif, la probabilité qu’un ordinateur ait une durée de vie inférieure à t années, notée p(X ≤ t), est donnée par :
.
1. Déterminer λ sachant que p(X > 5) = 0,4.
2. Dans cette question, on prendra λ = 0,18.
Sachant qu’un ordinateur n’a pas eu de panne au cours des 3 premières années, quelle est, à 10−3 près, la probabilité qu’il ait une durée de vie supérieure à 5 ans ?
3. Dans cette question, on admet que la durée de vie d’un ordinateur est indépendante de celle des autres et que p(X > 5) = 0,4.
a. On considère un lot de 10 ordinateurs.
Quelle est la probabilité que, dans ce lot, l’un au moins des ordinateurs ait une durée de vie supérieure à 5 ans ?
On donnera une valeur arrondie au millième de cette probabilité.
b. Quel nombre minimal d’ordinateurs doit-on choisir pour que la probabilité de l’évènement « l’un au moins d’entre eux a une durée de vie supérieure à 5 ans » soit supérieure à 0,999 ?
Géométrie dans l’espace
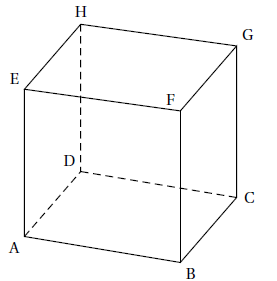
On considère le cube ABCDEFGH d’arête de longueur 1 représenté ci-dessous. Il n’est pas demandé de rendre le graphique avec la copie.
L’espace est rapporté au repère orthonormal
1. Démontrer que le vecteur de coordonnées (1 ; 0 ; 1) est un vecteur normal au plan (BCE).
2. Déterminer une équation du plan (BCE).
3. On note (Δ) la droite perpendiculaire en E au plan (BCE).
Déterminer une représentation paramétrique de la droite (Δ).
4. Démontrer que la droite (Δ) est sécante au plan (ABC) en un point R, symétrique de B par rapport à A.
5. a. Démontrer que le point D est le barycentre des points R, B et C affectés des coefficients respectifs 1, −1 et 2.
b. Déterminer la nature et les éléments caractéristiques de l’ensemble (S) des points M
de l’espace tels que
c. Démontrer que les points B, E et G appartiennent à l’ensemble (S).
d. Démontrer que l’intersection du plan (BCE) et de l’ensemble (S) est un cercle dont on précisera le rayon.
Arithmétique (spécialité)
Démontrer le théorème de Gauss en utilisant le théorème de Bézout.
On rappelle la propriété connue sous le nom de petit théorème de Fermat:
« Si p est un nombre premier et q un entier naturel premier avec p, alors ».
On considère la suite définie pour tout entier naturel n non nul par :
un = 2n +3n +6n −1.
1. Calculer les six premiers termes de la suite.
2. Montrer que, pour tout entier naturel n non nul, un est pair.
3. Montrer que, pour tout entier naturel n pair non nul, un est divisible par 4.
On note (E) l’ensemble des nombres premiers qui divisent au moins un terme de la suite (un).
4. Les entiers 2, 3, 5 et 7 appartiennent-ils à l’ensemble (E) ?
5. Soit p un nombre premier strictement supérieur à 3.
a. Montrer que: 6×2p−2 ≡ 3 (modulo p) et 6×3p−2 ≡ 2 (modulo p).
b. En déduire que 6up−2 ≡ 0 (modulo p).
c. Le nombre p appartient-il à l’ensemble (E) ?
Problème sur l’exponentielle
Partie A
On considère la fonction définie sur
par
.
1. Étudier les variations de la fonction g.
2. Déterminer le signe de g(x) suivant les valeurs de x.
3. En déduire que pour tout x de [0 ; +∞ [, ex − x > 0.
Partie B
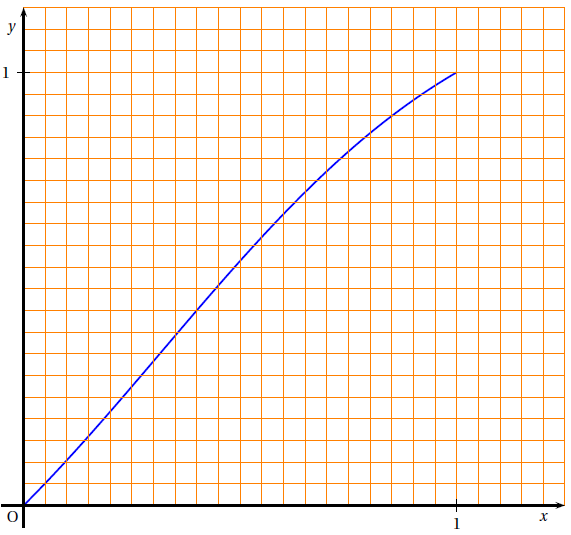
On considère la fonction f définie sur [0; 1] par
.
La courbe (C) représentative de la fonction dans le plan muni d’un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de l’épreuve.
On admet que f est strictement croissante sur [0; 1].
1. Montrer que pour tout x de [0; 1], f (x) Î [0 ; 1].
2. Soit (D) la droite d’équation y = x.
Montrer que pour tout x de [0; 1], .
Étudier la position relative de la droite (D) et de la courbe (C) sur [0; 1].
3. a. Déterminer une primitive de f sur [0; 1].
b. Calculer l’aire, en unités d’aire, du domaine du plan délimité par la courbe (C), la droite (D) et les droites d’équations x = 0 et x = 1.
Partie C
On considère la suite (un) définie par:
, pour tout entier naturel n.
1. Construire sur l’axe des abscisses les quatre premiers termes de la suite en laissant apparents les traits de construction.
2. Montrer que pour tout entier naturel n, un ≤ un+1 ≤ 1.
3. En déduire que la suite (un) est convergente et déterminer sa limite.
Probabilités
Pour réaliser une enquête, un employé interroge des personnes prises au hasard dans une galerie commerçante.
Il se demande si trois personnes au moins accepteront de répondre.
1. Dans cette question, on suppose que la probabilité qu’une personne choisie au hasard accepte de répondre est 0,1.
L’employé interroge 50 personnes de manière indépendante.
On considère les évènements :
A: « au moins une personne accepte de répondre »
B: « moins de trois personnes acceptent de répondre »
C: « trois personnes ou plus acceptent de répondre ».
Calculer les probabilités des évènements A, B et C. On arrondira au millième.
2. Soit n un entier naturel supérieur ou égal à 3. Dans cette question, on suppose que la variable aléatoire X qui, à tout groupe de n personnes interrogées indépendamment, associe le nombre de personnes ayant accepté de répondre, suit la loi de probabilité définie par :
a. Montrer que la probabilité qu’au moins trois personnes répondent est donnée par :
b. Calculer.
En donner l’arrondi au millième.
Cette modélisation donne-t-elle un résultat voisin de celui obtenu à la question 1?
3. On conserve le modèle de la question 2.
On souhaite déterminer le nombre minimum de personnes à interroger pour que la probabilité que trois d’entre elles au moins répondent soit supérieure ou égale à 0,95.
a. Étudier les variations de la fonction f définie sur R+ par
ainsi que sa limite en .
Dresser son tableau de variations.
b. Montrer que l’équation f(x) = 0, 95 admet une solution unique sur R+, et que cette solution est comprise entre 6,29 et 6,3.
c. En déduire le nombre minimum de personnes à interroger.
Géométrie et barycentre
L’espace est rapporté au repère orthonormal .
On considère le plan P d’équation 2x +y – 2z + 4 =0 et les points A de coordonnées (3; 2; 6),
B de coordonnées (1; 2; 4), et C de coordonnées (4 ; -2 ; 5).
1. a. Vérifier que les points A, B et C définissent un plan.
b. Vérifier que ce plan est le plan P.
2. a. Montrer que le triangle ABC est rectangle.
b. Écrire un système d’équations paramétriques de la droite Δ passant par O et perpendiculaire au plan P.
c. Soit K le projeté orthogonal de O sur P. Calculer la distance OK.
d. Calculer le volume du tétraèdre OABC.
3. On considère, dans cette question, le système de points pondérés S ={(O, 3), (A, 1), (B, 1), (C, 1)}
a. Vérifier que ce système admet un barycentre, qu’on notera G.
b. On note I le centre de gravité du triangle ABC. Montrer que G appartient à (OI).
c. Déterminer la distance de G au plan P.
4. Soit Γ l’ensemble des points M de l’espace vérifiant :
.
Déterminer Γ.
Quelle est la nature de l’ensemble des points communs à P et Γ ?
Les intégrales
1. Déterminer trois réels a, b, c tels que , pour tout :
.
2. Soit .
a. Calculer .
b. Soit f la fonction définie sur par
En intégrant par parties, calculer f(X) en fonction de X .
c. Montrer que
D'autres cours et exercices à consulter
- Bac de maths 2025 : sujets et corrigés du baccalauréat en PDF.
- Contrôle sur les fonctions et équations paramétriques en terminale
- Devoir surveillé en terminale sur les fonctions et courbes
- Contrôle sur les fonctions et nombres complexes en terminale
- Fonctions et variations : exercices de maths en 1ère corrigés en PDF.
- Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.
- Fonction linéaire : exercices de maths en 3ème corrigés en PDF.
- Dérivée d’une fonction : exercices de maths en terminale corrigés en PDF.