BREVET BLANC DE MATHÉMATIQUES
Session : 2022 – 2 heures
Exercice n° 1 (6 points)
Pour chacune des cinq affirmations suivantes, indiquer sur la copie, si elle est vraie ou fausse. On rappelle que chaque réponse doit être justifiée.
Affirmation n°1 :
« L’expression =(−5)(+1) a pour forme développée et réduite ».
Affirmation n°2 :
« Lorsque l’entier positif n est égal à 5, le nombre est un nombre premier ».
Affirmation n°3 :
« La somme de deux nombres entiers multiples de 5 est un multiple de 10 ».
Affirmation n°4 :
« L’expression prend la valeur =35 si =−2 ».
Affirmation n°5 :
« Les diagonales d’un rectangle ABCD de longueur 160 cm et de largeur 95 cm mesurent exactement 186 cm ».
Exercice n° 2 (5 points)
1) Justifier que le nombre 102 est divisible par 3.
2) On donne la décomposition en produit de facteurs premiers de 85 : .
Décomposer 102 en produit de facteurs premiers.
3) Donner 3 diviseurs non premiers du nombre 102. Un libraire dispose d’une feuille cartonnée de 85 cm × 102 cm.
Il souhaite découper dans celle-ci, en utilisant toute la feuille, des étiquettes carrées. Les côtés de ces étiquettes ont tous la même mesure.
4) Les étiquettes peuvent-elles avoir 34 cm de côté ? Justifier votre réponse.
5) Le libraire découpe des étiquettes de 17 cm de côté. Combien d’étiquettes pourra-t-il découper dans ce cas ?
Exercice n° 3 (7,5 points)
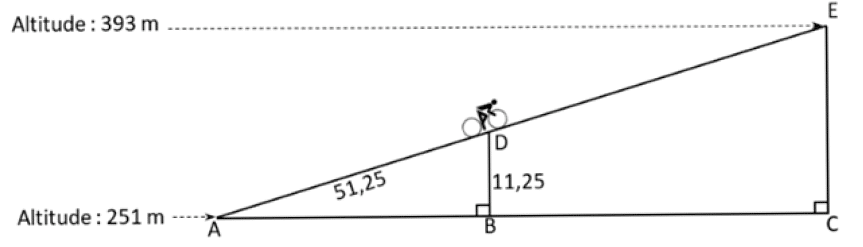
Aurélie fait du vélo en Angleterre au col de Hardknott.
Elle est partie d’une altitude de 251 mètres et arrivera au sommet à une altitude de 393 mètres.
Sur le schéma ci-dessous, qui n’est pas en vraie grandeur, le point de départ est représenté par le point A et le sommet par le point E.
Aurélie est actuellement au point D.
Les droites (AB) et (DB) sont perpendiculaires.
Les droites (AC) et (CE) sont perpendiculaires.
Les points A, D et E sont alignés.
Les points A, B et C sont alignés. AD = 51,25 m et DB = 11,25 m.
1) Justifier que le dénivelé qu’Aurélie aura parcouru, c’est-à-dire la hauteur EC, est égal à 142 m.
2) a) Prouver que les droites (DB) et (EC) sont parallèles.
b) Montrer que la distance qu’Aurélie doit encore parcourir, c’est-à-dire la longueur DE, est d’environ 596 m.
3) On utilisera pour la longueur DE la valeur 596 m.
Sachant qu’Aurélie roule à une vitesse moyenne de 8 km/h, si elle part à 9h55 du point D, à quelle heure arrivera-t-elle au point E ? Arrondir à la minute.
Exercice n° 4 (9 points)
Sur la figure ci-dessous qui n’est pas en vraie grandeur :
Les segments [OA] et [UI] se coupent en M.
MO = 21 mm, MA = 27 mm, MU = 28 mm, Ml = 36 mm et Al= 45 mm.
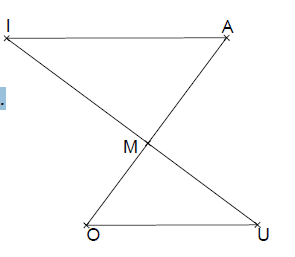
1) Prouver que les droites (OU) et (AI) sont parallèles.
2) Calculer la longueur OU.
3) Prouver que le triangle AMI est rectangle.
4) Déterminer, à un degré près, la mesure de l’angle .
Exercice n° 5 (6 points)
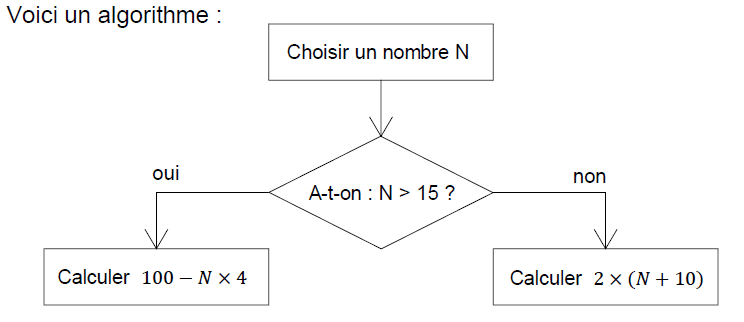
1) Justifier que si nombre N de départ choisi est égal à 18, le résultat final de cet algorithme est
28.
2) Quel résultat final obtient-on si on choisit 14 comme nombre N de départ ?
3) En appliquant cet algorithme, deux nombres de départ différents permettent d’obtenir 32
comme résultat final. Quels sont ces deux nombres ?
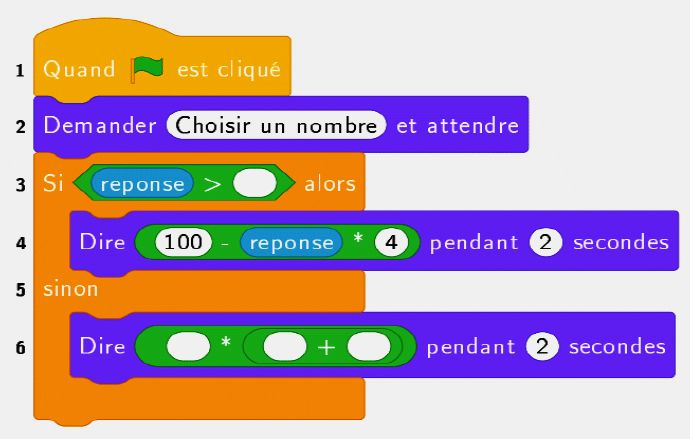
4) On programme l’algorithme précédent :
a) Recopier la ligne 3 en complétant les pointillés. Ligne 3 : Si Réponse > ………. alors.
b) Recopier la ligne 6 en complétant les pointillés. Ligne 6 : Dire ………. * ( …….. + ………. )
pendant 2 secondes.
Exercice n° 6 (6,5 points)
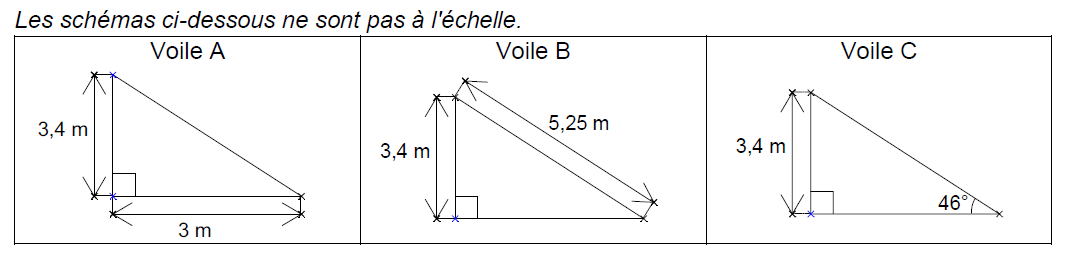
Pour son confort, Elise souhaite installer une voile d’ombrage triangulaire dans son jardin.
L’aire de celle-ci doit être de 6 m² au minimum.
Parmi les trois voiles suivantes, quelle(s) sont celle(s) qui pourraient convenir ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2022 : sujet et corrigé du brevet en PDF» au format PDF.
D'autres cours et exercices à consulter
- Brevet de maths 2019 en Grèce à télécharger en PDF
- France : brevet de maths 2023 avec sujet et corrigé en PDF.
- Brevet de maths 2023 : sujet pour réviser le brevet en ligne.
- Brevet de maths 2017 sujet 0
- Brevet Maths 2021 : sujet blanc pour réviser le brevet
- Antilles et Guyane 2019 : brevet de maths avec sujet et corrigé en PDF
- Brevet de maths 2019 en Nouvelle-Calédonie : sujet et corrigé en PDF
- Brevet blanc de maths 2025 avec sujet et corrigé n°1.