Equations et inéquations du second degré : cours en 1ère en PDF.

Sommaire

Les équations et inéquations du second degré dans un cours de maths en 1ère où nous aborderons la résolution avec le discriminant delta et la factorisation d’un polynôme du second de gré ainsi que l’étude de son signe. Dans cette leçon en première, nous étudierons l’interprétation graphique.

Dans tout ce chapitre, nous considérerons a un réel non nul.

I. Résolution de l’équation du second degré :

1. Définition et vocabulaire :

Définition :

Une équation du second degré, à une inconnue x, est une équation qui peut s’écrire sous la forme , où $a,\,b,\,c$ sont trois réels donnés avec $a\neq0$ .
Résoudre l’équation $ax^2+bx+c\,=\,0$ , c’est trouver tous les nombres tels que .
Un tel nombre p est dit solution ou encore racine de l’équation.

2. Résolution de l’équation du second degré :

Posons f(x) = ax²+bx+c avec $a\neq0$ .

2.1. Ecriture de f(x) sous forme canonique :

Définition :

Puisque $a\neq0$ , $f(x)=a(x^2+\frac{b}{a}x+\frac{c}{a})$ ou $x^2+\frac{b}{a}x=(x+\frac{b}{2a})^2-\frac{b^2}{4a^2}$

donc $f(x)=a[(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2}]$ .

Cette dernière écriture est appelée forme canonique de f.

2.2. Résolution de l’équation ax²+bx+c=0 :

Propriété :

On pose $\Delta\,=b^2-4ac$ ainsi $f(x)=a[(x+\frac{b}{2a})^2-\frac{\Delta\,}{4a^2}]$

Premier cas :

Si $\Delta\,<0$ alors $\frac{\Delta,}{4a^2}<0$ .

Le nombre entre crochets est strictement positif donc l’équation f(x)=0 n’a pas de solution.

Second cas :

Si $\Delta\,=0$ alors $f(x)=a(x+\frac{b}{2a})^2$ .

Puisque $a\neq,0$ , l’équation f(x)=0 a une solution et une seule :

$x=-\frac{b}{2a}$ .

Troisième cas :

Si $\Delta\,>0$ alors $\Delta\,=(\sqrt{\Delta\,})^2$ et :

$f(x)=a[(x+\frac{b}{2a})^2-\frac{\Delta\,}{4a^2}]\,\\f(x)=a[(x+\frac{b}{2a})^2-(\frac{\sqrt{\Delta}\,}{2a})^2]\,\\f(x)=a(x+\frac{b}{2a}+\frac{\sqrt{\Delta}\,}{2a})(x+\frac{b}{2a}-\frac{\sqrt{\Delta}\,}{2a})$

$f(x)=a(x-\frac{-b-\sqrt{\Delta}\,}{2a})(x-\frac{-b+\sqrt{\Delta}\,}{2a}-)$

Si l’on pose :

$x_1=\frac{-b-\sqrt{\Delta}\,}{2a}$ et $x_2=\frac{-b+\sqrt{\Delta}\,}{2a}$ alors .

Donc puisque $a\neq\,0$ , l’équation f(x)=0 a deux solutions distinctes x_1 et x_2 .

Définition :

Le nombre b^2-4ac est appelé discriminant de l’équation du second degré ou du trinôme .

On le note $\Delta$ ( lire « delta »).

Théorème :

a. Lorsque $\Delta\,<0$ , l’équation n’a pas de solution dans $\mathbb{R}$ .

b. Lorsque $\Delta\,=0$ , l’équation a une racine double : $x_1=\frac{-b\,}{2a}$ .

c. Lorsque $\Delta\,>0$ , l’équation a deux solutions :

$x_1=\frac{-b-\sqrt{\Delta}\,}{2a}$ et $x_2=\frac{-b+\sqrt{\Delta}\,}{2a}$ .

II. Factorisation et signe du trinôme :

1. Factorisation du trinôme :

Nous avons vu, au cours de la démonstration du théorème 1 que si

$\Delta\,>0$ alors .

Théorème 2 : factorisation du trinôme.

Lorsque l’équation f(x)=ax²+bx+c=0 a deux solutions x_1 et x_2 ( dans le cas $\Delta\,>0$ ) alors,

2. Signe du trinôme :

Théorème

Lorsque $\Delta\,<0$ , est toujours du signe de a.
Lorsque $\Delta\,=0$ , est du signe de a
Lorsque $\Delta\,<0$ , est du signe de a, sauf lorsque x est entre les racines, auquel cas f(x) et a sont de signes contraires.

Application :

Pour résoudre une inéquation du second degré, on détermine le signe du trinôme associé.

III. Représentations graphiques des fonctions trinômes :

Définition :

La courbe de la fonction $f : x \mapsto ax^2+bx+c$ est une parabole. Cette parabole est tournée vers le haut lorsque a>0 et tournée vers le bas lorsque a<0 .

Synthèse :

Exemples :

Résoudre

Solution :

$\Delta\,=-3$ puisque $\Delta\,<0$ , le trinôme n’a pas de racine dans $\mathbb{R}$ .

De plus a=1 donc a>0 ainsi pour tout réel et $S=\mathbb{R}$ .

Résoudre l’inéquation du second degré $-x^2+3x-2\,\geq\,\,0$ .

Nous avons $\Delta\,=3^2-4\times \,(-1)\times \,(-2)=9-8=1$ .

L’équation a deux racines qui son t:

$x_1=\frac{-3+\sqrt{1}}{2\times \,(-1)}=\frac{-2}{-2}=1$ = 1 et $x_2=\frac{-3-\sqrt{1}}{2\times \,(-1)}=\frac{-4}{-2}=2$ .

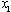
Nous avons donc ainsi l’ensemble solution de l’inéquation du second degré $-x^2+3x-2\,\geq\,\,0$ est l’intervalle $[1\,;2]$ .

4.3/5 - (118 votes)

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «equations et inéquations du second degré : cours de maths en 1ère en PDF.» au format PDF.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Equations et inéquations du second degré : cours de maths en 1ère en PDF.

I. Résolution de l’équation du second degré :

1. Définition et vocabulaire :

2. Résolution de l’équation du second degré :

2.1. Ecriture de f(x) sous forme canonique :

2.2. Résolution de l’équation ax²+bx+c=0 :

II. Factorisation et signe du trinôme :

1. Factorisation du trinôme :

2. Signe du trinôme :

III. Représentations graphiques des fonctions trinômes :

Télécharger et imprimer ce document en PDF gratuitement :

D'autres cours et exercices à consulter

I. Résolution de l’équation du second degré :

1. Définition et vocabulaire :

2. Résolution de l’équation du second degré :

2.1. Ecriture de f(x) sous forme canonique :

2.2. Résolution de l’équation ax²+bx+c=0 :

II. Factorisation et signe du trinôme :

1. Factorisation du trinôme :

2. Signe du trinôme :

III. Représentations graphiques des fonctions trinômes :

Télécharger et imprimer ce document en PDF gratuitement :

D'autres cours et exercices à consulter

Cours de première

Exercices de première

Nos applications