Brevet de maths 2017 avec sujet blanc sur le théorème de Pythagore et la trigonométrie ainsi qu’un QCM et utilisation du tableur et calcul du volume d’un solide.
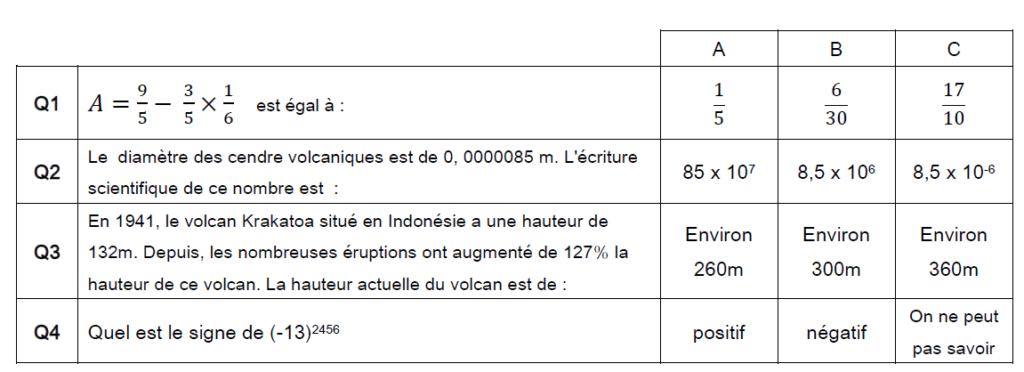
Exercice N°1: QCM 5 points.
Cet exercice est un QCM (questionnaire à choix multiples).
Pour chaque ligne du tableau, une seule affirmation est juste.
Sur ta copie, indiquer le numéro de la question et recopier l’affirmation juste.
On ne demande pas de justifier.
Exercice N°2: Motif et Scratch (d’après sujet zéro DNB 2017) 4 points.
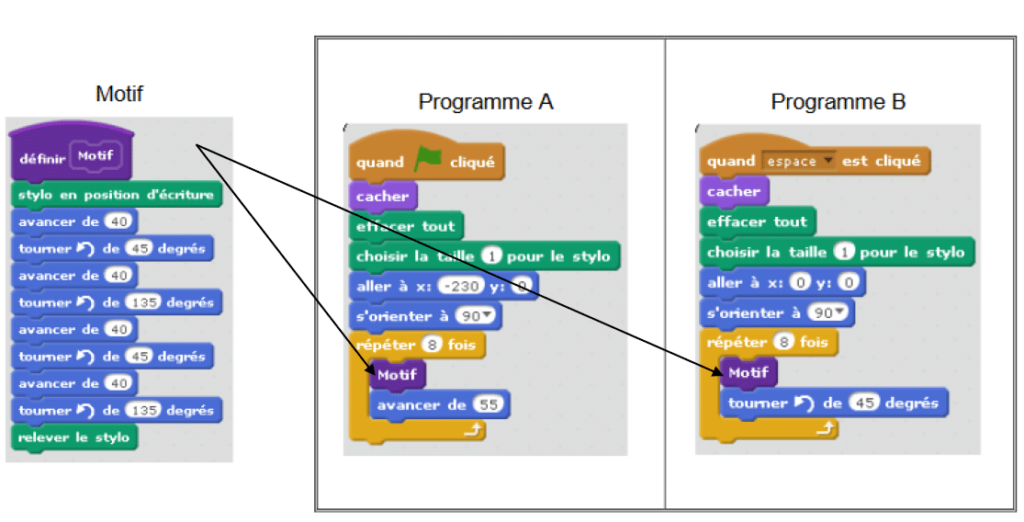
1. Pour réaliser la figure ci-dessus, on a défini un motif en forme de losange et on a utilisé l’un des deux programmes A et B ci-dessous.
Déterminer lequel et indiquer par une figure à main levée le résultat que l’on obtiendrait avec l’autre programme.
2. Combien mesure l’espace entre deux motifs successifs ?
3. On souhaite réaliser la figure ci-dessous:
Pour ce faire, on envisage d’insérer l’instruction 
Où faut-il insérer cette instruction ?
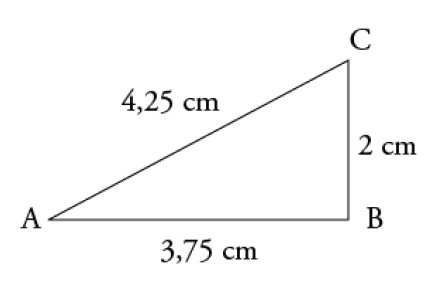
Exercice N°3: Rectangle ou non rectangle… 3 points.
Le triangle ABC est-il rectangle en B ? Justifier la réponse.
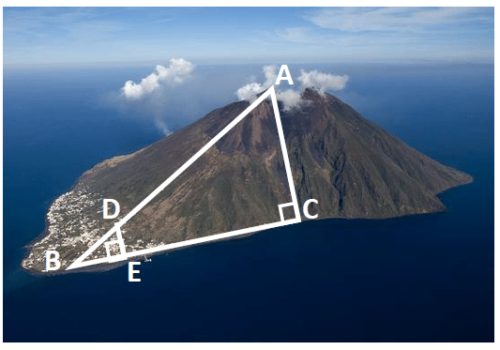
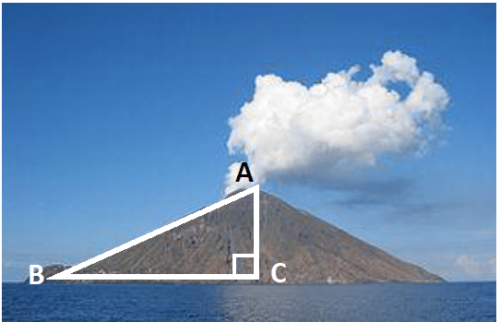
Exercice N°4: Hauteur du Stromboli … 6 points
Trois personnes mesurent la hauteur de cet impressionnant volcan, Le Stromboli, situé en Italie, en utilisant des méthodes différentes.
1. La méthode de Cécile et Lydia
Cécile se couche par terre face au volcan.
Lydia se tient debout, perpendiculaire au sol, entre elle et le volcan, à l’endroit où l’oeil B de Cécile, la tête D de Lydia et le haut A du volcan sont alignés.
La distance BC entre l’oeil B de Cécile et le bas C du volcan est 1200 m.
La distance BE entre l’oeil B de Cécile et les pieds E de Lydia est 2,20 m.
La taille DE de Lydia est 1,70 m.
Aide Cécile et Lydia à calculer la hauteur AC du volcan.
Tu donneras la valeur arrondie au mètre près.
2. La méthode d’Adélaïde …
Adélaïde se couche par terre face au Volcan (du côté village)
Elle place un instrument de mesure d’angles devant son oeil B.
La distance BA entre l’oeil B d’Adélaïde et le haut A du volcan est 1385 m.
L’angle mesure 42°.
Aide Adélaïde à calculer la hauteur AC du volcan.
Tu donneras la valeur arrondie au mètre près.
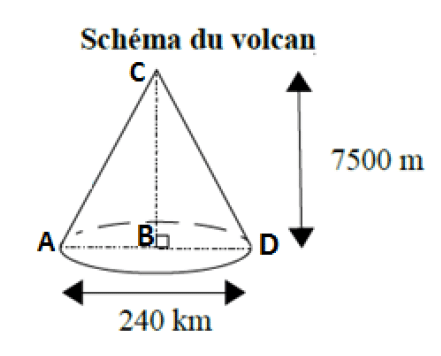
Exercice N°5: Le Piton de la Fournaise … 5 points
On assimile le Piton de la Fournaise à un cône de hauteur 7500 m et sa base fait 240 km de diamètre.
1. Calculer le volume de ce cône en .
On rappelle la formule pour calculer le volume d’un cône : .
2. Calculer la longueur de la pente CD que va descendre la lave. Arrondir le résultat au millième.
3. L’âge du volcan (en années) est égal à
avec le volume moyen de lave émise chaque année soit
.
Calculer l’âge du Piton de la Fournaise. Arrondir le résultat à l’année.
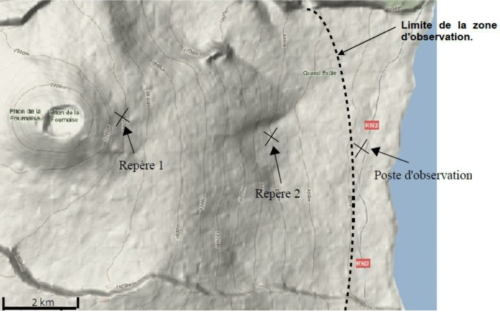
Exercice N°6: Piton de la Fournaise (suite)… 6 points
Voici l’image satellite du Piton de la Fournaise lors d’une éruption :
1. La lave a mis 4 minutes et 10 secondes pour parcourir la distance entre le repère 1 et le repère 2.
Calculer sa vitesse moyenne en m/s.
2. Les scientifiques observent que la lave atteint le repère 2 à 17h 15min 25s.
Si on suppose que sa vitesse moyenne reste de 16 m/s, en combien de temps les scientifiques doivent-ils évacuer le poste d’observation ?
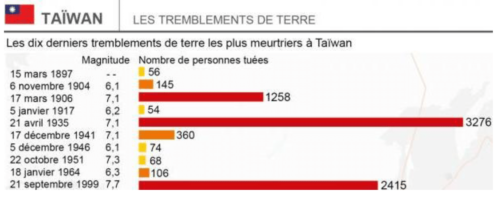
Exercice N°7: Séisme à Taiwan 4 points.
1. En t’aidant du document ci-dessus, détermine en quelle année il y a eu le tremblement de terre le plus meurtrier à Taïwan ?
2. En t’aidant du document ci-dessus, détermine en quelle année il y a eu le tremblement de terre de plus forte magnitude ?
3. Calculer la magnitude moyenne des tremblements de terre les plus meurtriers à Taiwan entre 1904 et 1999.
4. Calculer le nombre moyen de personnes tuées à cause des tremblements de terre à Taïwan entre 1897 et 1999.
5. On souhaite calculer le nombre total de personnes tuées à cause des derniers 10 tremblements de terre les plus meurtriers à Taïwan, en utilisant le tableur.
Quelle formule doit-on écrire dans la cellule L2 ?
Exercice N°8: Nuage de cendre 12 points.
CONSEIL : bien lire TOUS les documents avant de se lancer dans la résolution pour sélectionner toutes les informations utiles.
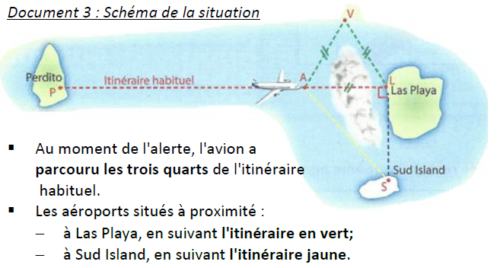
Un nuage de cendres provenant de l’éruption d’un volcan oblige un avion à se détourner de son itinéraire habituel.
Question
Aider le commandant de bord à choisir un nouvel itinéraire :
Peut-il contourner le nuage et poser l’avion sur un aéroport situé à proximité ?
Peut-il faire demi-tour ?
Document 1 : des distances
- Perdito – Las Playa : 1920 km
- Las Playa – Sud Island : 550 km
Document 2 : Le vol prévu Perdita – Las Playa
- Passagers : 140
- Heure de départ : 15h40
- Heure d’arrivée 18h04
- Carburant au départ de Perdito : 9000 L
- Consommation : 400L pour 100 km
Si le travail n’est pas terminé, laisser tout de même une trace de la démarche sur votre copie.
Elle sera prise en compte dans l’évaluation.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2017 : sujet blanc pour réviser le DNB en 3ème.» au format PDF.
D'autres cours et exercices à consulter
- Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.
- Brevet de maths 2021 : sujet blanc pour réviser
- Brevet 2017 : sujet blanc de maths à effectuer en ligne.
- Brevet de maths 2017 : sujet blanc pour réviser en ligne.
- Brevet Amérique du Nord 2021 maths : sujet et corrigé en PDF.
- Brevet de maths 2018 en Amérique du Nord – sujet et corrigé
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Amérique du nord 2016 : sujet du brevet de maths