Durée de l’épreuve : 2 heures 100 points
Ce sujet comporte 6 exercices.
Dès que le sujet vous est remis, assurez-vous qu’il soit complet.
L’usage de tout modèle de calculatrice, avec ou sans mode examen, est autorisé.
L’utilisation du dictionnaire est interdite.
Exercice 1 (20 points)
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1) Scratch souhaite rejoindre un ami, mais il a oublié la fin du trajet. Il décide de finir son trajet en prenant, aux intersections, à droite ou à gauche au hasard.
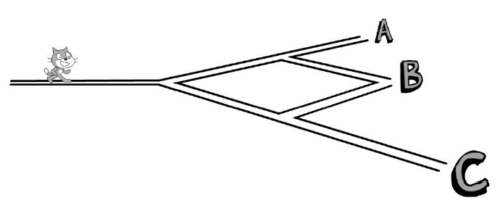
Affirmation 1 : La probabilité qu’il arrive en A, en B ou en C est la même.
2) On suppose qu’une éolienne produit 5 GWh d’électricité par an et qu’une personne a besoin de 7 000 kWh d’électricité par an. (Wh : Watt-heure)
Affirmation 2 : Une éolienne ne couvre pas les besoins en électricité de 1000 personnes pour un an.
3) Voici quatre nombres : 45 % ; ; 0,5 ;
.
Affirmation 3 : Ces quatre nombres sont rangés dans l’ordre croissant.
4) L’histogramme ci-dessous représente la répartition des salaires dans une entreprise :
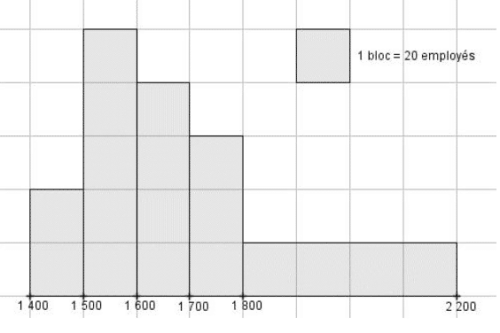
Affirmation 4 : Plus de 40 % des employés ont un salaire au moins égal à 1 700 €.
Exercice 2 (16 points)
Les baleines émettent des sons, de fréquences comprises entre 10 Hz et 10 kHz, qui se propagent dans l’eau à une vitesse d’environ 1500 m\s.
L’étude des chants des baleines a pour but d’élucider leur possible signification ; sélection du partenaire sexuel et communication sociale sont des hypothèses envisagées.
1. Convertir la vitesse de propagation de ces sons en km/h.
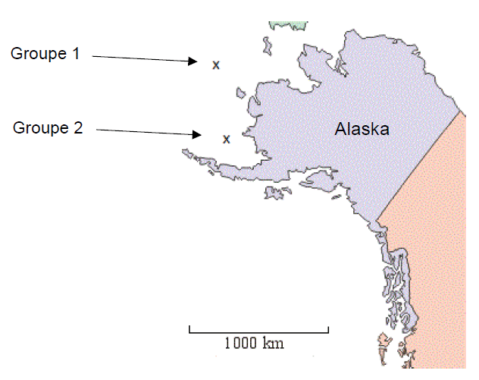
2. Deux groupes de baleines situées au large de l’Alaska communiquent entre eux.
2.1. Calculer la distance séparant les deux groupes de baleines.
Vous donnerez le résultat arrondi à 50 km près.
2.2. Combien de temps met une onde sonore émise par une baleine du groupe 1 pour parvenir aux baleines du groupe 2 ? Vous donnerez le résultat arrondi à la minute.
3. Le dessin ci-dessous donne une idée de la taille d’une baleine bleue par rapport à celle d’un homme.
En considérant que le plongeur sur l’image a une taille égale à 1,75 m, calculer la taille approximative de la baleine représentée ci-dessous. Vous donnerez le résultat arrondi au mètre près.
La démarche et les traces de recherche seront valorisés et prises en compte dans la notation.
Exercice 3 (16 points)
On demande à quinze élèves d’une classe A et à dix élèves d’une classe B de compter le nombre de SMS qu’ils envoient pendant un week-end. Le lundi on récupère les résultats dans un tableur.
1. Calculer le nombre moyen et le nombre médian de SMS envoyés pendant le week-end par ces élèves de la classe A.
2. Quelles formules ont pu être écrites dans les cellules Q3 et R3 du tableur ?
3. Calculer le nombre moyen de SMS envoyés pendant le week-end par ces 25 élèves des classes A et B.
4. Calculer le nombre médian de SMS envoyés pendant le week-end par ces 25 élèves des classes A et B.
Exercice 4 (18 points)
1. Le responsable du plus grand club omnisport de la région a constaté qu’entre le 1er janvier 2010 et le 31 décembre 2012 le nombre total de ses adhérents a augmenté de 10 % puis celui-ci a de nouveau augmenté de 5 % entre le 1er janvier 2013 et le 31 décembre 2015.
Le nombre total d’adhérents en 2010 était de 1000.
1.1. Calculer, en justifiant, le nombre total d’adhérents au 31 décembre 2012.
1.2. Calculer, en justifiant, le nombre total d’adhérents au 31 décembre 2015.
1.3. Martine pense qu’au 31 décembre 2015, il devrait y avoir 1150 adhérents car elle affirme : « une augmentation de 10 % puis une autre de 5 %, cela fait une augmentation de 15 % « . Qu’en pensez-vous ? Expliquez votre réponse.
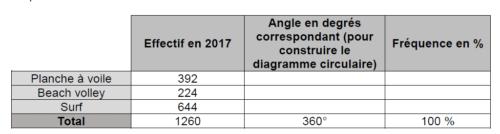
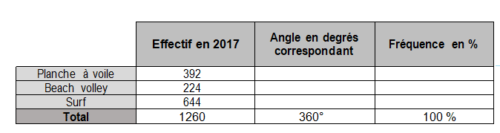
2. Au 1er janvier 2017, les effectifs étaient de 1260 adhérents.
Voici le tableau de répartition des adhérents en 2017 en fonction de leur sport de prédilection.
2.1. Compléter sur l’annexe, page 8, la colonne intitulée « Angle en degrés correspondant ». (Pour expliquer votre démarche, vous ferez figurer sur votre copie les calculs correspondants.)
2.2. Pour représenter la situation, construire un diagramme circulaire de rayon 4 cm.
2.3. Compléter sur l’annexe la colonne « Fréquence en % ». (Pour expliquer votre démarche, vous ferez figurer sur votre copie les calculs correspondants. Vous donnerez le résultat arrondi au centième près.)
Exercice 5 (16 points)
Les deux parties de cet exercice sont indépendantes.
Mario, qui dirige un centre de plongée sous-marine en pleine expansion, décide de construire un bâtiment pour accueillir ses clients lors de la pause déjeuner. Celui-ci sera constitué d’un rez-de-chaussée climatisé servant de réfectoire et d’un étage non climatisé qui pourra être utilisé pour le stockage du matériel de plongée.
Pour finir d’établir son budget, il ne lui reste plus qu’à choisir un modèle de climatisation adapté et à calculer la quantité nécessaire de tuiles pour couvrir le toit de sa construction qu’il a schématisé ci-dessous.
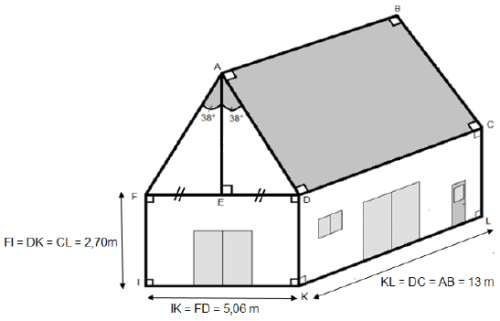
Document 1 : Croquis réalisé par Mario.
Le croquis n’est pas réalisé à l’échelle.
Les deux pentes (ou versants) de la toiture forment un angle de mesure 76° qui est partagé en deux parties égales de 38°.
Document 2 : Tuiles plates choisies par Mario pour recouvrir son toit.
Prévoir 26 tuiles par m²
Prix : 0,65 euro l’unité.
1. PARTIE 1 : Calcul du budget correspondant aux tuiles.
1.1. Calculer AD. Vous donnerez le résultat arrondi au centimètre près.
1.2. Calculer AE. Vous donnerez le résultat arrondi au centimètre près.
1.3. En déduire le prix des tuiles nécessaires à la couverture des deux pentes du toit.
2. PARTIE 2 : Choix d’un climatiseur adapté.
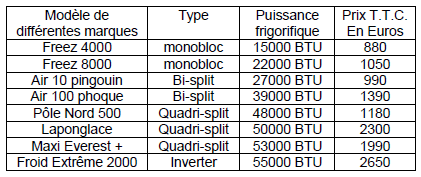
À l’aide des documents, faire un choix de climatiseur raisonné, adapté et le moins cher possible pour climatiser le rez-de-chaussée du bâtiment, c’est dire à dire le réfectoire.
Document 3 : Comment choisir un climatiseur ?
Etape 1 : Connaître la puissance frigorifique nécessaire.
Celle-ci dépend du volume des pièces à refroidir.
La puissance de froid s’exprime en BTU qui est une unité de mesure frigorifique.
Le tableau ci-dessous fait la correspondance entre le volume du bâtiment à refroidir et la puissance en BTU nécessaire.
Etape 2 : Choisir le climatiseur le plus adapté.
Exercice 6 (14 points)
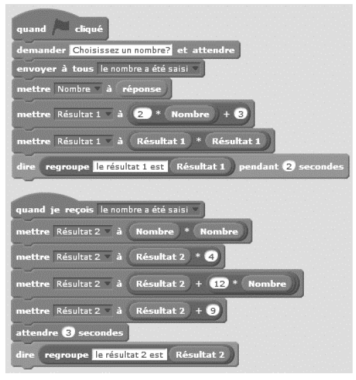
Voici un script saisi par Alice dans un logiciel d’algorithmique.
1. Alice a choisi 3 comme nombre, calculer les valeurs de Résultat 1 et de Résultat 2 ? Justifier en faisant apparaître les calculs réalisés.
2. Généralisation
2.1. En appelant le nombre choisi dans l’algorithme, donner une expression littérale traduisant la première partie de l’algorithme correspondant à Résultat 1.
2.2. En appelant le nombre choisi dans l’algorithme, donner une expression littérale traduisant la deuxième partie de l’algorithme correspondant à Résultat 2.
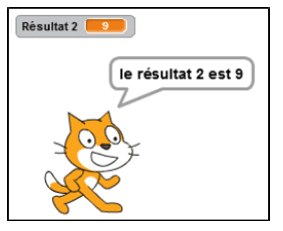
3. Trouver le ou les nombres choisis par Alice qui correspondent au résultat affiché ci-dessous.
ANNEXE
Exercice 4 question 2 :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2019 : sujet blanc pour réviser le DNB 2019» au format PDF.
D'autres cours et exercices à consulter
- Brevet de maths 2018 à Pondichéry : sujet et corrigé en PDF
- Brevet Amérique du Nord 2021 maths : sujet et corrigé en PDF.
- Brevet de maths 2024 : sujet et corrigé pour réviser
- Brevet blanc de maths 2025 avec sujet et corrigé n°1.
- Asie Pacifique 2017 : sujet et corrigé du brevet maths en PDF
- Brevet de maths 2017 – sujet et corrigé du rattrapage en Polynésie
- Brevet de maths 2024 blanc n° 1 : sujet et corrigé en PDF.
- Brevet de maths 2017 : sujet blanc