La proportionnalité et les pourcentages dans un cours de maths en 4ème où nous aborderons la définition de la proportionnalité ainsi que le coefficient et le tableau de proportionnalité. Nous verrons la règle du produit en croix ainsi que le calcul de la quatrième proportionnelle, puis, nous terminerons cette leçon en quatrième avec l’interprétation graphique … Lire la suite
La translation et la rotation dans un cours de maths en 4ème au cycle 4.Nous étudierons la définition et les propriétés de ces deux transformations du plan.Les propriétés de conservation de l’alignement, des longueurs, des aires, des milieux et des mesures d’angles dans cette leçon destinées aux élèves de quatrième.
I. La translation
Définition
Définition :
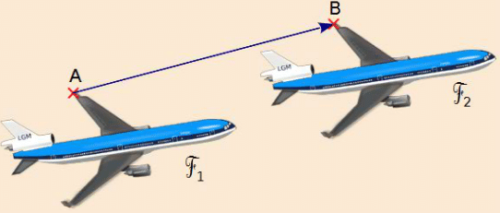
Lorsque l’on fait glisser la figure sans la faire tourner, de manière à ce que A arrive en B,elle se superpose avec la figure .
On dit que la figure est l’image de la figure par la translation qui transforme A en B.
2. Image d’un point et d’un segment
Propriété n° 1 :
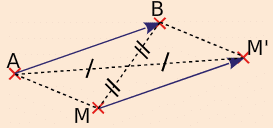
L’image du point M, par la translation qui transforme A en B, est le point M’ tel queles segments [MB] et [AM’] ont le même milieu.
Si les points ne sont pas alignés alors ABM’M est un parallélogramme.
Propriété n° 2 :
L’image d’un segment par une translation est un segment qui lui est parallèle et de même longueur.
Exemple :
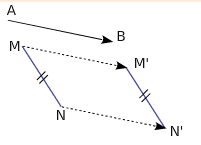
Dans la translation qui transforme A en B, le segment [MN] a pour image le segment [M’N’].
Donc les segments [MN] et [M’N’] sont parallèles et de même longueur.
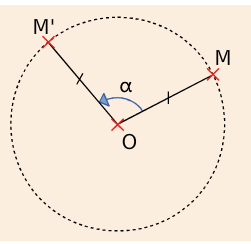
II. La rotation
Définition
Définition :
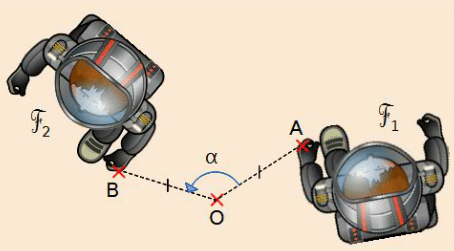
Lorsque l’on fait tourner la figure autour du point O, d’un angle de mesure , dans le sens contraire des aiguilles d’une montre, elle se superpose avec la figure .On dit que la figure est l’image de la figure par la rotation de centre O et d’angle .
Remarque :
Dans tout ce chapitre, le sens de rotation sera toujours le sens trigonométrique (sens contraire du déplacement des aiguilles d’une montre).
La rotation de centre O et d’angle 180° est la symétrie centrale de centre O.
2. Image d’un point
Propriété :
On considère O et M deux points distincts.
L’image du point M par la rotation de centre O et d’angle est le point M’ tel que :
et .
III. Les propriétés de la translation et de la rotation
Propriété :
La translation et la rotation conservent les longueurs, l’alignement, les aires, les milieux et les mesures d’angle.
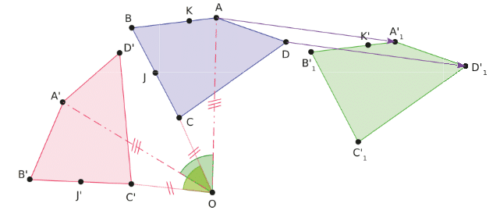
Exemple :
Le quadrilatère A’B’C’D’ est l’image de ABCD par la rotation de centre O et d’angle 60°.
Le quadrilatère est l’image de ABCD par la translation qui transforme en .
Les aires et les périmètres des trois quadrilatères sont égaux..
Les points A,B,K sont alignés donc leurs images sont également alignées.
Le point J est le milieu du segment [BC] donc son image J’ par la rotation est le milieu du segment [B’C’].
L’angle est l’image de l’angle par la translation, ils ont donc la même mesure.
L’angle est l’image de l’angle par la translation, ils ont donc la même mesure.
Pyramides et cônes de révolution dans un cours de maths en 4ème de géométrie dans l’espace. Nous verrons la définition d’une pyramide et d’un cône ainsi que de sa base et la génératrice. Nous construirons le patron de ces solides et nous effectuerons des conversions de volumes. Puis, nous terminerons cette leçon en quatrième avec … Lire la suite
Le calcul littéral et la double distributivité dans un cours de maths en 4ème faisant intervenir la définition d’une expression littérale ou algébrique, savoir développer ou factoriser une expressions. Puis nous terminerons cette leçon en quatrième avec les propriétés de la simple et double distributivité. I. Développer et réduire une expression. 0. Préambule: règle des … Lire la suite
Les puissances de 10 dans un cours de maths en 4ème qui fait intervenir les définitions et les différentes propriétés. Utilisation des formules et de l’écriture scientifique d’un nombre relatif dans cette leçon en quatrième et utiliser les règles de calculs sur les puissances. Introduction : Point de vue scientifique : Taille de l’univers (ordre de … Lire la suite
Les fractions dans un cours de maths en 4ème où nous aborderons les quatre opérations (addition, soustraction, multiplication et division) et la résolution de problèmes dans cette leçon destinés aux élèves de quatrième au cycle 4.Ce chapitre intervient après avoir assimilé les nombres relatifs. I. Définition et vocabulaire : 1. Définition : Définition : Une … Lire la suite
Le théorème de Pythagore avec un cours de maths en 4ème faisant intervenir la partie directe et réciproque du théorème ainsi que la racine carrée d’un nombre positif et l’interprétation géométrique du théorème de Pythagore dans cette leçon en quatrième. 0-Introduction : un peu d’histoire…. Point de vue historique : Pythagore de Samos, né vers … Lire la suite
Les nombres relatifs avec un cours de maths en 4ème qui porte sur les quatre opérations dont la règle des signe et sa généralisation ainsi que l’addition et la soustraction de nombres relatifs ainsi que du calcul du quotient dans cette leçon en quatrième. I. Multiplier deux nombres relatifs. 0. Préambule: règle des signes. Afin … Lire la suite
L’initiation à la démonstration à travers un cours de maths en 4ème. Ce document permet d’aborder la notion de propriété directe et réciproque ainsi que les contre-exemple. Elle est adressée aux enseignants et élèves de collège en quatrième.
I. S’APPROPRIER LE SENS DE LA LOCUTION : « Si … alors … »
En mathématiques, pour savoir si une proposition est vraie ou fausse, on utilise certaines règles.
Une proposition mathématique est soit vraie, soit fausse.
Donner des exemples qui vérifient une proposition donnée ne suffit pas à prouver que cette proposition est vraie.
Donner un exemple qui ne vérifie pas une proposition donnée suffit à prouver que cette proposition est fausse. Cet exemple est appelé « contre-exemple »
Dans le domaine géométrique, une constatation ou des mesures sur un dessin ne suffisent pas à prouver qu’une proposition est vraie.
II. Consignes de travail
Je vous propose ci-dessous 7 propositions mathématiques écrites à partir de la locution « Si…alors… ».
Je vous demande ,premièrement, de prendre position individuellement sur chacune des propositions ( dire si la proposition est vraie ou fausse) puis, d’en débattre au sein du groupe pour éventuellement adopter une position commune. Et, lorsque cela est signalé, d’énoncer la proposition réciproque et de valider ou non cette proposition.
Quels que soient les points A, B et I, si AI = IB alors le point I est milieu du segment [AB] (étude
de la réciproque).
Quelles que soient les droites D et D’, si D est perpendiculaire à D’ alors les droites D et D’ se coupent en un point (étude de la réciproque).
Quel que soit le nombre décimal relatif, si ce nombre est inférieur à 3 alors il est inférieur à 9.
Quels que soient les points A, B et I, si les points A, I et B sont alignés alors I est un point du segment [AB] (étude de réciproque).
Quels que soient les nombres entiers, si la somme de deux nombres est paire alors ces deux nombres sont pairs.
Quel que soit le quadrilatère, si c’est un carré alors c’est un rectangle.
Quels que soient les nombres entiers relatifs, si deux nombres sont consécutifs alors leur produit est un nombre pair.
Puissances d’un nombre relatif avec un cours de maths en 4ème où nous aborderons la définition d’une puissance puis les différentes règles de calculs comme l’inverse d’une puissance, le produit et le quotient de puissances dans cette leçon en quatrième. Puissance entière d’un nombre relatif : 1. Puissances positives : désigne un nombre relatif et un … Lire la suite
Les équations du premier degré à une inconnue à travers un cours de maths en 4ème à télécharger en PDF. Dans cette leçon, l’élève devra connaître la définition d’une équation, d’une inconnue mais également, du premier et second membre. Développer des compétences dans la résolution d’équation en déterminant la solution en utilisant les différentes propriétés … Lire la suite
×12
L'équipe Mathovore
Contenu mis à jour quotidiennement
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
