La proportionnalité : cours de maths en 5ème à télécharger en PDF

La proportionnalité dans un cours de maths en 5ème où nous étudierons les grandeurs proportionnelles ainsi que des tableaux de proportionnalité ainsi que les différentes propriétés et la détermination du coefficient de proportionnalité. la règle du produit en croix et la calcul de la quatrième proportionnelle. Nous terminerons cette leçon en cinquième avec le calcul de pourcentages et d’échelle.

I. Situation de proportionnalité

1.Grandeurs proportionnelles

Définition :

On dit que deux grandeurs sont proportionnelles quand les valeurs prises par l’une s’obtiennent en multipliant celles prises par l’autre par un même nombre non nul, appelé coefficient de proportionnalité.

Exemples :

$\star$ La longueur du côté et le périmètre d’un carré sont proportionnels car le périmètre d’un carré s’obtient en multipliant la longueur d’un côté par 4.

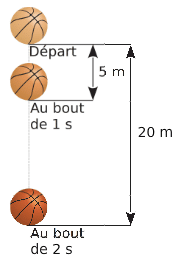
$\star$ Voici la distance parcourue par un ballon en chute libre.

En 1 seconde, il parcourt 5 m et en 2 secondes, il parcourt 20 m.Pour passer de la durée de chute à la distance parcourue, on ne multiplie pas par un même nombre, donc la durée de chute et la distance parcourue ne sont pas proportionnelles.

2.Tableau de proportionnalité

Propriété 1 :

Quand on regroupe les valeurs prises par deux grandeurs proportionnelles, on obtient un tableau de proportionnalité.

Propriété 2 :

Dans un tableau de proportionnalité, les nombres de la seconde ligne s’obtiennent en multipliant les nombres correspondants de la première ligne par le coefficient de proportionnalité.

Exemple :

A la vitesse de 70 km/h, une voiture consomme 5 L aux 100 km.

$\cdot$ La consommation de carburant et la distance parcourue sont proportionnelles.

$\cdot$ A cette vitesse, quand la voiture parcourt une distance de 1 km, elle consomme 0,05 L (5:100).

$\cdot$ On peut regrouper ces résultats dans un tableau de proportionnalité.

$\cdot$ A cette vitesse, la consommation, en litres de carburant, est égale au produit du nombre de kilomètres parcourus par 0,05 qui est le coefficient de proportionnalité.

Dans cette situation, ce coefficient permet de calculer la consommation à partir du kilomètre parcouru : par exemple, à cette vitesse et pour 15 km, la consommation sera 15 x 0,05 = 0,75 L.

Propriété 3 :

On peut compléter un tableau de proportionnalité à l’aide des propriétés de linéarité.

II. Applications

1.Appliquer un pourcentage

Exemple :

Lors de soldes, une réduction de 15 % est accordée sur les articles d’un magasin.

Cela signifie que :

la réduction et le prix initial de l’un article sont proportionnels;
si le prix initial est de 100 €, alors la réduction est de 15 €.

On cherche la réduction d’un article coûtant 80 €.On regroupe ces données dans un tableau de proportionnalité.

Le coefficient de proportionnalité est 0,15.

Donc la réduction recherchée est égale à 80 x 0,15 = 12 €.

Propriété :

Pour calculer $x$ % d’une quantité, on multiplie cette quantité par $x$ puis on divise par 100.

Exemple :

25 % de 350 est égal à $(25\times 350)\div 100=87,5$

2.Echelle

Définition :

L’échelle d’une carte ou d’un plan est le coefficient de proportionnalité qui permet de passer

des distances réelles aux distances correspondantes sur la carte ou le plan, exprimées dans la même unité.

$Echelle=\frac{distance\,sur\,le\,plan}{distance\,reelle}$ .

Exemple :

Ce dessin représente le plan d’un hélicoptère.

Dans la réalité, il a pour hauteur 3,9 m, donc l’échelle est :

$Echelle=\frac{distance\,sur\,le\,plan}{distance\,reelle}=\frac{2,6}{390}=\frac{1}{150}$ .

Ce qui signifie que 1 cm sur le plan correspond à 150 cm dans la réalité.

La longueur réelle de l’appareil est donc $x=7,75\times 150\approx 1162,5\,cm\approx 11,63\,cm$ .