Exercice 1 – Calculer la distance d’un point à un plan
Calculer la distance du point M(5; 2; −3) au plan d’équation x + 4y + 8z = −2.
Exercice 2 – Un plan formé par trois points
Soient A(1; −1; 1), B(0; 2; −1) et C(−1; 1; 0).
Montrer que A, B et C forment un plan puis déterminer x afin que (x; 3; 4) soit normal à (ABC).
Exercice 3 – Plans orthogonaux
Les plans P : 2x − y + z + 9 = 0 et Q : x + y − z − 7 = 0 sont-ils orthogonaux ?
Exercice 4 – Equation cartésienne d’un plan
Déterminer une équation cartésienne du plan P passant par A(−2; 1; 3) et orthogonal
à (BC) où B(1; −2; 2) et C(4; 1; −1).
Exercice 5 – Déterminer l’équation cartésienne d’un plan
Déterminer une équation cartésienne du plan contenant A(2; −1; 1) et orthogonal au
vecteur (3; −4; 2).
Exercice 6 – Vecteur normal et plan
Le vecteur (6; −2; 4) est-il normal au plan d’équation −3x + y − 3z = 1 ?
Exercice 7 – Vecteur normal d’un plan
Déterminer un vecteur normal au plan d’équation 31x + 37y + 41z + 43 = 0.
Exercice 8 – Calcul de la mesure d’un angle
On se place dans un repère orthonormal.
Soient A(−1; 1; 2), B(0; 1; 0) et C(2; 0; 3).
Calculer une mesure approchée de l’angle .
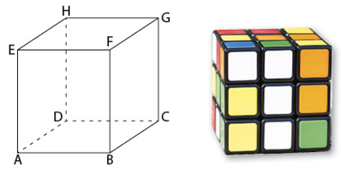
Exercice 9 – Produit scalaire et cube
Soit ABCDEFGH un cube d’arête a.
Calculer :
Exercice 10 – Tétraèdre régulier
Soit ABCD un tétraèdre régulier d’arête a.
Calculer
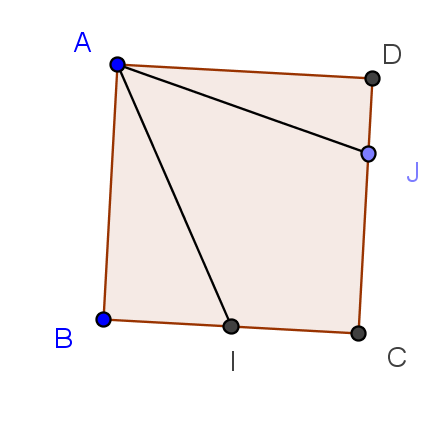
Exercice 11 – Etudier un carré
ABCD est un carré de coté 8 unités.
Les points I et J sont définis pas et
.
1. Exprimer le produit scalaire de deux façons différentes .
2. Déterminer , puis la mesure de cet angle en radians .
Exercice 12 – Ensemble de points
ABC est un triangle équilatérale de côté de longueur .
Quel est l’ensemble des point M tels que :
Exercice 13 :
Pour calculer le produit scalaire de deux vecteurs de l’espace, on choisit trois points O, M, N tels
que et
, puis on calcule
dans un plan
contenant les points O, M, N.
On modélise un Rubik’s cube par un cube ABCDEFGH d’arête 1 représenté ci-dessous.
1.a) Dans chaque cas, calculer le produit scalaire.
• (utiliser le plan (ADE))
•
• (utiliser le plan du rectangle AFGD).
b) En déduire que dans l’espace, on a également .
2.Les vecteurs et
sont tels que
et
.
a) Choisir des représentants des vecteurs et
dont les extrémités appartiennent à un même plan.
b) Calculer alors .
3.Calculer .
Que peut-on dire des vecteurs et
?
On dit alors que les droites (EA) et (DC) sont orthogonales.
Exercice 14 :
ABCDEFGH est un cube d’arête 1.
On se place dans le repère .
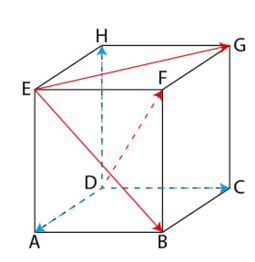
a) Justifier que les droites (DA), (DC) et (DH) sont perpendiculaires deux à deux et
que DA =DC =DH.
On dit que le repère est orthonormé.
b) et
sont deux vecteurs de coordonnées respectives
et
dans le repère
orthonormé .
• Exprimer les vecteurs et
en fonction des vecteurs
,
et
.
• Développer le produit scalaire en utilisant le fait que dans l’espace, le produit scalaire est encore bilinéaire et symétrique.
En déduire que .
2.a) Utiliser la formule précédente pour démontrer que les vecteurs et
sont orthogonaux.
b) Démontrer que les vecteurs et
sont orthogonaux.
On dit alors que la droite (DF) est orthogonale au plan (EBG).
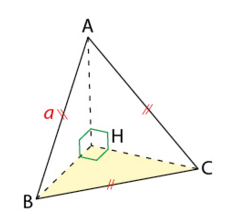
Exercice 15 :
ABCH est un tétraèdre tel que ABC est un triangle équilatéral d’arête a (avec a > 0),
et les autres faces sont des triangles rectangles en H.
a) Déterminer le produit scalaire .
b) Développer et réduire le produit scalaire .
c) Exprimer la distance du point A au plan (BHC) en fonction de a.
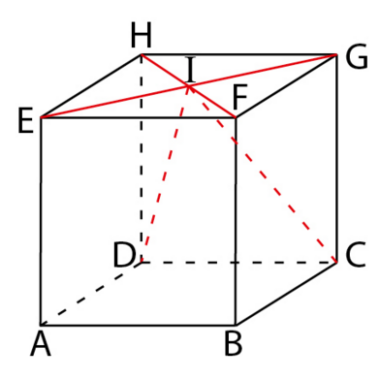
Exercice 16 :
ABCDEFGH est un cube d’arête a et I est le centre de la face EFGH.
a) Donner la nature du triangle DCI.
b) Calculer le produit scalaire .
c) Exprimer ce produit scalaire en fonction de et en déduire la mesure en degré de l’angle
.
Arrondir au dixième.
Exercice 17 :
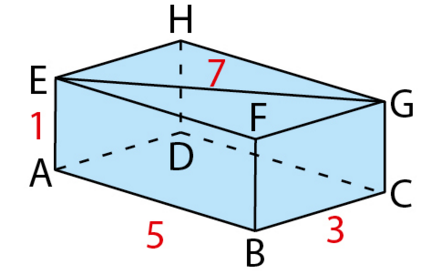
ABCDEFGH est un parallélépipède rectangle.
Calculer :
.
.
.
Exercice 18 :
Alix affirme : « Dans un repère orthonormé, les vecteurs et
sont orthogonaux. ».
A-t-il raison ?
Exercice 19 :
Dans un repère orthonormé, déterminer mentalement celui de ces vecteurs qui est orthogonal au vecteur .
Exercice 20 :
Dans un repère orthonormé de l’espace, étudier mentalement l’orthogonalité de et
.
.
.
.
.
.
Exercice 21 :
Dans un repère orthonormé de l’espace le vecteur a pour coordonnées (1;2;4).
Calculer .
Exercice 22 :
Dans un repère orthonormé de l’espace, A et B sont les points de coordonnées respectives
(3;1;0) et (5;0;1).
Calculer .
Exercice 23 :
et
sont deux vecteurs de l’espace tels que
,
et
.
Calculer .
Exercice 24 :
et
sont deux vecteurs de l’espace tels que AB = 5, AC = 8 et
.
Calculer .
Exercice 25 :
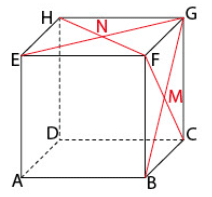
ABCDEFGH est un cube de côté .
Les points M et N sont les centres des faces BCGF et EFGH.
a) Vérifier que .
b) Calculer et
.
c) En déduire la valeur du produit scalaire .
Exercice 26 :
Dans un repère orthonormé de l’espace, on donne les coordonnées des vecteurs et
.
Calculer .
Exercice 27 :
Dans un repère orthonormé, on considère les points A(1;-1;0), B(-2,2,6), C(3,1,- 8)
et le vecteur .
1.Vérifier que les points A,B,C ne sont pas alignés.
2.a) Démontrer que le vecteur est normal au plan ABC.
b) Déterminer une équation cartésienne du plan (ABC).
Exercice 28 :
Dans un repère orthonormé, A et B sont les points de coordonnées respectives
(3,2,0) et (5,1,-1) .
est le plan passant par A et orthogonal à la droite (AB).
a. Donner un vecteur normal au plan .
b. En déduire une équation cartésienne du plan .
Exercice 29 :
Soit les points de l’espace A(-4;4;0), B(4;0;-4) et C(1;1;1)
1. Déterminer une représentation paramétrique de la droite (AB).
2. Déterminer la distance entre le point C et son projeté orthogonal H sur la droite (AB).
H est tel que les droites (CH) et (AB) sont perpendiculaires.
Exercice 30 :
Soit P le plan passant par le point A (4; 8;-4) et dirigé par les vecteurs (2 ; -1 ; 3) et
(4; 1; -3).
1. Démontrer que (0 ; 3 ; 1) est un vecteur normal au plan P.
2. Déterminer un vecteur normal au plan P, tel que la troisième coordonnée de
, soit égale 7.
3. Déterminer un vecteur normal du plan P, tel que la deuxième coordonnée de
, soit égale – 1.
4. Est-il possible de trouver un vecteur normal au plan P dont la première coordonnée est égale à 4 ?
Exercice 31 :
Soit (d) la droite dont une représentation paramétrique est :
avec
.
Déterminer une équation du plan P passant par le point A(8;-5 ;3) et perpendiculaire à la droite (d).
Exercice 32 :
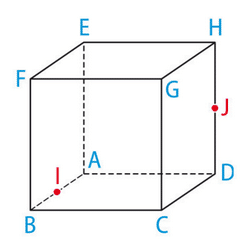
ABCDEFGH est un cube.
Le point I est le milieu de [AB] et le point J est le milieu de [DH].
On se place dans le repère orthonormé .
1. Déterminer les coordonnées des points I, Jet G.
2. Justifier que les points I, J et G définissent un plan.
3. a. Déterminer des réels a, b et c tels que soit un vecteur normal au plan (IJG).
b. En déduire une équation du plan (IJG).
Exercice 33 :
Soit P le plan d’équation .
Les droites et
sont définies par une représentation paramétrique donnée ci-dessous :
et
avec
.
1. Le plan P et la droite (d1) sont-ils sécants ?
2. Déterminer l’intersection du plan P et de la droite (d2).
Exercice 34 :
On considère les points A(0;4;1), B(1;3;0), C(2;-1;-2) et D(7;- 1;4).
1. Démontrer que les points A, B et C ne sont pas alignés.
2. Soit la droite passant par le point D et de vecteur directeur
(2 ; —1 ; 3).
a. Démontrer que la droite est orthogonale au plan (ABC).
b. En déduire une équation cartésienne du plan (ABC).
c. Déterminer une représentation paramétrique de la droite .
d. Déterminer les coordonnées du point H, intersection de la droite et du plan (ABC).
3. Soit le plan d’équation x + y + z = 0 et
le plan d’équation x +4y +2=0.
a. Démontrer que les plans et
sont sécants.
b. Vérifier que la droite (d), intersection des plans et
a pour représentation paramétrique
c. La droite (d) et le plan (ABC) sont-ils sécants ou parallèles ?