Exercice 1 :

Dans un repère orthonormé de l’espace, et sont les droites de représentations paramétriques
respectives :

a) Montrer que les droites et ne sont pas parallèles.
b) Étudier l’intersection de et en résolvant un système d’équations.

Exercice 2 :

et sont deux droites de représentations paramétriques respectives :

Indiquer oralement les coordonnées d’un point et d’un vecteur directeur de chacune des droites et .

Exercice 3 :

est la droite de représentation paramétrique :

Déterminer mentalement les coordonnées de quatre points de la droite .

Exercice 4 :

On donne les points :

  et

Parmi ces systèmes, une représentation paramétrique de la droite (AB) est :

Exercice 5 :

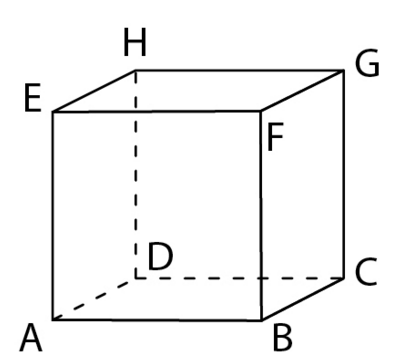
ABCDEFGH est le cube représenté ci-dessous.
a) Déterminer les coordonnées de chacun des sommets dans le repère .

b) Déterminer une représentation paramétrique de chacune des droites (AG) et (BH).

Exercice 6 :

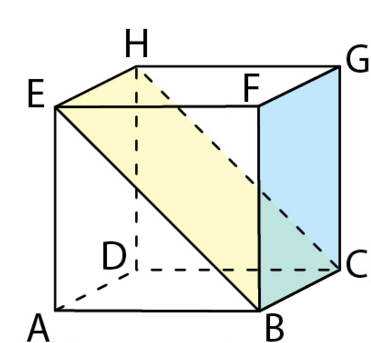
ABCDEFGH est le cube représenté ci-contre.
Pour chacun des plans ci-dessous, indiquer oralement deux vecteurs normaux.
a) (ABC)

b) (BCF)

c) (ADF)

Exercice 7 :

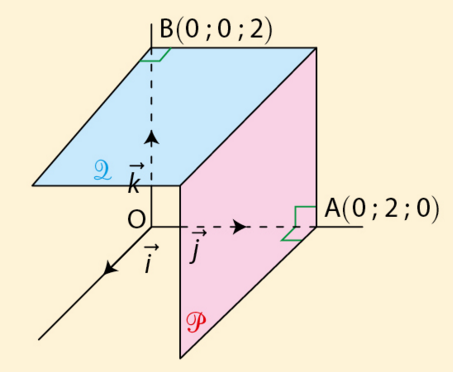
Déterminer une équation cartésienne du plan :
a) coloré en rouge passant par le point A et orthogonal à l’axe des ordonnées ;
b) coloré en bleu passant par le point B et orthogonal à l’axe des côtes.

Exercice 8 :

On se place dans le repère orthonormé .
a) Déterminer les coordonnées d’un vecteur normal au plan (BCF), puis au plan (BCE).

b) Déterminer une équation cartésienne du plan (BCF), puis du plan (BCE).

Exercice 9 :

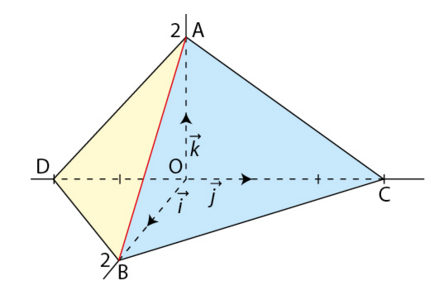
On a placé quatre points A, B, C, D dans le repère orthonormé ci-dessous.

a) Lire les coordonnées des points A, B, C, D.
b) Démontrer que le vecteur est normal au plan (ABC) ; puis que le vecteur est normal au plan (ABD).
c) Déterminer une équation cartésienne du plan (ABC), puis du plan (ABD).
d) Alix affirme « Le point appartient à l’un des deux plans ».

A-t-elle raison ?

Exercice 10 :

et sont les droites de représentations paramétriques respectives :

       et     

Déterminer mentalement lequel de ces systèmes on est amené à résoudre pour déterminer l’inter
section de et .

      et 

Exercice 11 :

Voici les représentations paramétriques respectives de deux droites et sécantes.
Déterminer leur point d’intersection.

       et     

Exercice 12 :

et sont les droites de représentations paramétriques respectives :

       et     

a) Démontrer que et ne sont pas parallèles.
b) Démontrer que et   ne sont pas coplanaires en résolvant un système d’équations.

Exercice 13 :

a et b désignent des nombres réels.

On donne les points .

On se propose de déterminer a et b afin que les points A, B, C soient alignés.

a) Déterminer les coordonnées des vecteurs et .
b) Montrer que les points A, B, C sont alignés si, et seulement si,

c) Résoudre ce système et conclure en donnant les coordonnées de A, B, C.

Exercice 14 :

est un plan d’équation cartésienne :
 (avec a et b nombres réels).
Existe-t-il des nombres a et b tels que les points  appartiennent
au plan .

Exercice 15 :

 est le plan d’équation cartésienne :

.
A est le point de coordonnées
a) Déterminer une représentation paramétrique de la droite passant par A et perpendiculaire au plan .
b) En déduire les coordonnées du point H, projeté orthogonal du point A sur le plan .