Produit scalaire : cours de maths en 1ère à télécharger en PDF.

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Le produit scalaire dans le plan dans un cours de maths en 1ère où nous étudierons la définition et les différentes propriétés du produit scalaire. Dans cette leçon en première, nous verrons la relation entre le produit scalaire et la notion d’orthogonalité. Puis, nous terminerons par des applications avec le cosinus d’un angle, le théorème d’Al-Kashi et le théorème de la médiane.

I. Différentes expressions du produit scalaire :

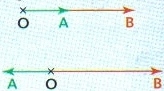
1. Vecteurs colinéaires :

Définition :

soient $\vec{u}$ et $\vec{v}$ deux vecteurs colinéaires non nuls, tels que

$\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ .

• Si $\vec{u}$ et $\vec{v}$ sont de même sens : $\vec{u}.\vec{v}=OA\times OB$ .

• Si $\vec{u}$ et $\vec{u}$ sont de sens contraires : $\vec{u}.\vec{v}=OA\times OB$ .

• Si $\vec{u}=\vec{0}$ ou $\vec{v}=\vec{0}$ alors $\vec{u}.\vec{v}=0$ .

• $\vec{u}.\vec{u}=||\vec{u}||$ est le carré scalaire du vecteur $\vec{u}$

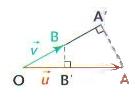
2. Vecteurs quelconques :

Propriété 1 :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls tels que

$\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ .

Alors :

$\fbox{\vec{u}.\vec{v}=OA'\times OB=OA\times OB'}$ .

A’ et B’ sont respectivement les projetés orthogonaux de A sur (OB) et de B sur (OA).

3. Propriétés :

Propriété 2 :

Soient (x;y) et (x’;y’) les coordonnées respectives des vecteurs $\vec{u}$ et $\vec{v}$ dans un repère orthonormé quelconque.

$\fbox{\vec{u}.\vec{v}\,=\,x.x'+y.y'}$ .

II. Produit scalaire et orthogonalité :

Définition :

Dire que $\vec{u}$ et $\vec{v}$ sont deux vecteurs orthogonaux signifie que :

• Soit $\vec{u}=\vec{0}$ ou $\vec{v}=\vec{0}$ ;

• Soit (OA) $\perp$ (OB), avec $\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ non nuls.

2. Propriété :

Propriété :

$\fbox{\vec{u}\perp\vec{v}\,\,\Longleftrightarrow\,\,\vec{u}.\vec{v}=0}$ .

III. Propriétés du produit scalaire :

Propriétés :

Propriétés :

Soient $\vec{u}\,,\,\vec{v},\,\vec{w}$ trois vecteurs et k un nombre réel.

• $\vec{u}.\vec{v}=\vec{v}.\vec{u}$ (symétrie).

• $(k\vec{u}).\vec{v}=\vec{u}.(k\vec{v})=k(\vec{u}.\vec{v})$ (linéarité)

• $(\vec{u}+\vec{v}).\vec{w}=\vec{u}.\vec{w}+\vec{v}.\vec{w}$ (linéarité)

• $\vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$ (linéarité)

• $(\vec{u}+\vec{v})^2=\vec{u}^2+2\vec{u}.\vec{v}+\vec{v}^2$ (identité remarquable)

• $(\vec{u}-\vec{v})^2=\vec{u}^2-2\vec{u}.\vec{v}+\vec{v}^2$ (identité remarquable)

• $(\vec{u}-\vec{v})(\vec{u}+\vec{v})=\vec{u}^2-\vec{v}^2$ (identité remarquable)

IV. Applications du produit scalaire :

1. Produit scalaire et cosinus :

Propriété :

Soit $\vec{u}$ et $\vec{v}$ non nuls.

$\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}||\times cos(\vec{u},\vec{v})$

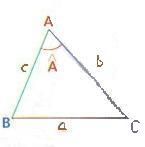
2. Théorème d’Al-Kashi :

Théorème :

Soit ABC un triangle tel que AB=c, AC=b et BC=a.

On a :

$a^2\,=\,b^2+c^2-2bc\times cos(\widehat{A})$
$b^2\,=\,a^2+c^2-2ac\times cos(\widehat{B})$
$c^2\,=\,a^2+b^2-2ab\times cos(\widehat{C}$

3. Théorème de la médiane :

Théorème :

Soient A et B deux points distincts et I le milieu du segment [AB] .

Pour tout point M, :

$\fbox{ MA^2\,+MB^2\,=\,2MI^2\,+\,\frac{AB^2}{2}}$