Les fonctions : cours de maths en 1ère à télécharger en PDF.

Les généralités sur les fonctions numériques dans un cours de maths en 1ère qui fait intervenir les tableaux de variation d’une fonction ainsi que sa représentation graphique.

Dans cette leçon en première, nous étudierons le fonctions racine carrée et la valeur absolue ainsi que le sens de variation des fonctions u+k.

I. La fonction racine carrée :

Définition :

La fonction f définie sur $[0;+\infty[$ , qui à tout nombre réel positif x associe sa racine carrée $\sqrt{x}$ , est appelée fonction racine carrée.

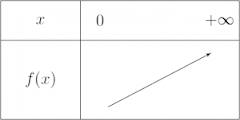
1. Sens de variation de la fonction racine carrée :

Propriété :

La fonction $f:x \mapsto \sqrt{x}$ est croissante sur $[0;+\infty[$ .

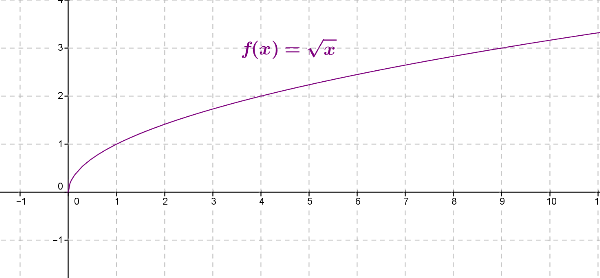
Courbe représentative de la fonction racine carrée :

Tableau de variation :

Démonstration :

u et v désignent deux nombres réels positifs tels que $u\leq v$ .

Les deux nombres positifs $\sqrt{u}$ et $\sqrt{v}$ sont rangés dans le même ordre que leurs carrés.

$(\sqrt{u} )^2=u$ et $(\sqrt{v} )^2=v$ .

Or $0\leq u\leq v$ donc $\sqrt{0}\leq \sqrt{u}\leq \sqrt{v}$ , c’est à dire $f(u)\leq f(v)$ .

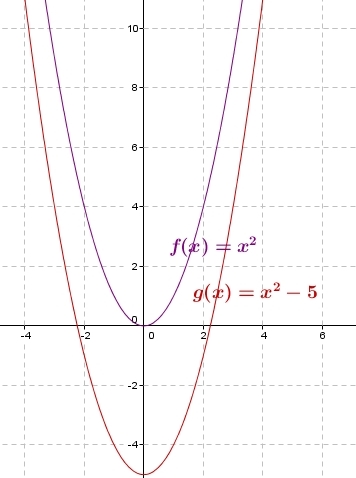
2. Représentation graphique de la fonction racine carrée :

Dans un repère orthogonal, $\zeta$ désigne la courbe représentative de la fonction racine carrée.

Propriété :

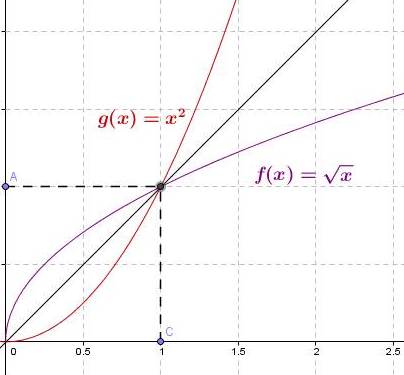
Dans un repère orthonormé, la courbe représentative $\zeta$ de la fonction racine carrée et la courbe représentative $\rho$ de la fonction carré sur $[0;+\infty[$ sont symétriques par rapport à la droite d’équation y=x.

Démonstration :

x et y désignent deux nombres réels positifs.

$y=\sqrt{x}$ équivaut à $x=y^2$ , c’est à dire :

$M(x;y)$ appartient à $\zeta$ si, et seulement si, $M'(y;x)$ appartient à $\rho$ .

Propriété :

Pour tout nombre réel x de l’intervalle $[0;1]$ , $x^2\leq x\leq \sqrt{x}$ .

Pour tout nombre réel x de l’intervalle $[1;+\infty[$ , $\sqrt{x}\leq x\leq x^2$ .

II. La fonction valeur absolue :

1. Valeur absolue d’un nombre réel :

Définition :

Sur une droite graduée d’origine O, x est l’abscisse d’un point M.

La valeur absolue du nombre réel x, noté $\left | x\right |$ , est la distance OM.

Exemples :

$\left | 7,3\right |=7,3$

$\left | -5,2\right |=5,2$

$\left | 1-\sqrt{2}\right |=\sqrt{2}-1$

Propriété :

Pour tout nombre réel x,

2. La fonction valeur absolue :

Définition :

La fonction $f$ définie sur $\mathbb{R}$ , qui à tout nombre réel x associe sa valeur absolue $\left | x\right |$ , est appelée fonction valeur absolue.

a. Sens de variation :

Propriété :

La fonction valeur absolue est décroissante sur $]-\infty;0]$ et croissante sur $[0;+\infty[$ .

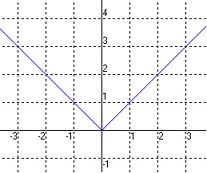
b. Représentation graphique :

Dans un repère orthogonal, la courbe représentative de la fonction valeur absolue est la réunion des demi-droites d’équations y=x sur $[0;+\infty[$ et y= – x sur $]-\infty;0]$ .

Propriété :

Dans un repère orthogonal, la courbe représentative $\zeta$ de la fonction valeur absolue est symétrique par rapport à l’axe des ordonnées.

Démonstration :
x et y désignent deux nombres réels.

M(x;y) appartient à la courbe $\zeta$ si, et seulement si, $y=\left | x \right |$ .

III. sens de variation des fonctions 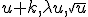$u+k,\lambda u,\sqrt{u}$ et $\frac{1}{u}$ :

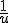1. Fonctions 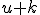$u+k$ et $\lambda u$ :

Propriété :

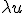u est une fonction définie sur un intervalle I et k un nombre réel.

Les fonctions u et u+k ont le même sens de variation sur l’intervalle I.

Propriété :

u est une fonction définie sur un intervalle I et $\lambda$ un nombre réel non nul.

– Si $\lambda >0$ alors les fonctions $u$ et $\lambda u$ ont le même sens de variation sur I.

– Si $\lambda <0$ alors les fonctions $u$ et $\lambda u$ ont des sens de variation contraires sur I.

Exemples :
La fonction $x \mapsto x^2 -5$ a le même sens de variation sur $\mathbb{R}$ que la fonction carrée.

La fonction $x \mapsto -2\sqrt{x}$ est décroissante sur $[0;+\infty[$ .

2. Fonctions 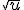$\sqrt{u}$ et $\frac{1}{u}$ :

Propriété :

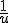u est une fonction définie sur un intervalle I telle que, pour tout nombre réel x de I, $u(x)\geq 0$ .

La fonction $x \mapsto\sqrt{u (x )}$ , notée $\sqrt{u }$ , a le même sens de variation que u sur l’intervalle I.

Propriété :

u est une fonction définie sur un intervalle I telle que, pour tout nombre réel x de I, $u(x)\neq 0$ et $u(x)$ garde le même signe.

La fonction $x \mapsto \frac{1}{u(x)}$ , notée $\frac{1}{u }$ , a un sens de variation contraire à celui de u sur I.