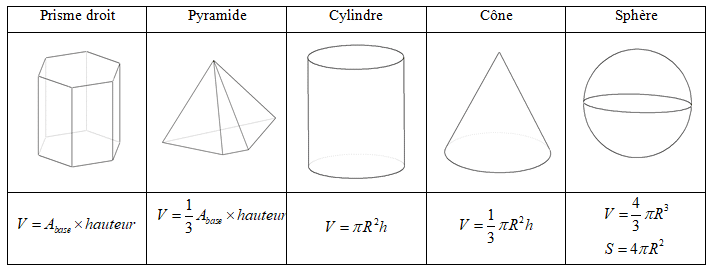🧮Cours de Mathématiques
1ère • Lycée
Position relative de deux droites dans l’espace
📖 Temps de lecture : 5 min
🎯 Niveau : Lycée
📱 Format : Gratuit
📄 PDF : Disponible
La géométrie dans l’espace à travers un cours de maths en 1ère avec la notion de perspective cavalière ainsi que les différentes positions relatives de deux droites dans l’espace et de plans. Cette leçon est à télécharger au format PDF en première.
I. Perspective cavalière.
Définitions et vocabulaire :
Dans une représentation d’un solide en perspective cavalière :
- une figure représentée dans un plan vu de face est représentée en vraie grandeur, sans changer sa forme ;
- deux droites parallèles sont représentées par deux droites parallèles ;
- des points alignés sont représentés par des points alignés ;
- le milieu d’un segment est représenté par le milieu du segment dessiné ;
- les éléments visibles sont en traits pleins, ceux qui sont cachés sont en pointillés ;
- une droite perpendiculaire au plan frontal est représentée par une droite faisant un angle aigu avec l’horizontale du support de représentation ;
- toute longueur sur une telle droite est multipliée par un coefficient inférieur à 1.
II. Positions relatives de droites et de plans
1.Règles d’incidence
Règles :
- Par deux points distincts il passe une unique droite ;
- Par trois points non alignés A, B, C, il passe un unique plan noté (ABC) ;
- Si un plan contient deux points A et B, alors il contient tous les points de la droite (AB) ;
- Si (d) est une droite et A un point non situé sur (d), il existe un unique plan contenant (d) et A.
2.Positions relatives de deux droites.
Propriété :
Deux droites peuvent être :
- Coplanaires : elles sont situées dans un même plan (elles sont alors sécantes ou parallèles)
- Non coplanaires : et dans ce cas elles n’ont aucun point en commun.
3.Positions relatives d’une droite et d’un plan.
Propriété :
Une droite peut être :
- Contenue dans un plan si elle passe par deux points du plan ;
- Sécante au plan, si elle n’a qu’un seul point commun avec ce plan (voir ci-contre) ;
- Parallèle au plan si elle n’a aucun point commun avec le plan.
4.Position relatives de deux plans.
Propriété :
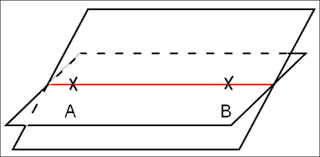
Deux plans sont soit parallèles, s’ils n’ont aucun point en commun, soit sécants et dans ce cas leur intersection est une droite (ils ont donc une infinité de points d’intersection).
Exemple de plans sécants, selon la droite (UV).
III- Parallélisme dans l’espace.
1.Parallélisme entre des droites.
Propriétés :
- Si deux droites sont parallèles à une même troisième, alors elles sont parallèles entre elles.
- Si deux droites sont parallèles alors tout plan qui coupe l’une coupe aussi l’autre.
2. Parallélisme entre deux plans.
Propriétés :
- Si deux plans sont parallèles alors tout plan parallèle à l’un est aussi parallèle à l’autre.
- Si deux droites sécantes (d) et (d’) du plan (P) sont parallèles à deux droites sécantes et du plan (P’) alors les deux plans (P) et (P’) sont parallèles.
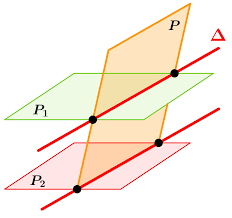
- Si deux plans (P) et (P’) sont parallèles, alors tout plan qui coupe l’un coupe aussi l’autre et les droites d’intersection (d) et (d’) sont parallèles.
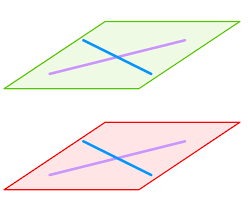
Exemple de plans parallèles déterminés par deux paires de droites sécantes.
3.Parallélisme entre droites et plans.
Propriétés :
- Si deux plans sont parallèles et si une droite est parallèle au premier plan alors elle est aussi parallèle au second.
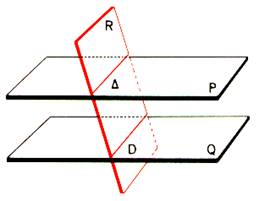
- Si la droite (d) est parallèle au plan (P) alors tout plan contenant (d) et sécant à (P) le coupe selon une droite parallèle à (d). Démonstration
- Si la droite (d) est parallèle à une droite du plan (P) alors (d) est parallèle au plan (P) .Démonstration
- Si les plans (P) et (P’) sont sécants selon la droite et si (d) est une droite parallèle aux deux plans (P) et (P’) alors les droites et (d) sont parallèles.
IV. Calculs en géométrie dans l’espace
1.Orthogonalité entre une droite et un plan
Propriété :
- Une droite est perpendiculaire à un plan si elle est orthogonale à deux droites sécantes de ce plan.
- Si une droite est perpendiculaire à un plan alors elle est orthogonale à toutes les droites de ce plan.
2.Aires et volumes des solides classiques