Suites : exercices de maths en terminale corrigés en PDF.

✏️Exercices

Terminale • Lycée

Suites numériques

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les suites numériques à travers des exercices de maths en terminale corrigés. Vous avez également le choix de réfléchir sur les énoncés à difficultés croissantes afin de progresser et combler vos lacunes dans la matière.

Exercice 1 – suites arithmétiques et géométriques
1. Soit la suite arithmétique $(U_n)$ de raison r=-2 et telle que $U_{10}=25$ .
a. Calculer $U_{50}$ .
b. Calculer $S_{10}=U_1+U_2+...+U_{10}$ .
2. Soit la suite géométrique $(V_n)$ de raison $q=\frac{1}{2}$ et telle que $V_8=\frac{3}{8}$ .
a. Calculer $V_{20}$ .
b. Calculer $S_9=V_1+V_2+...+V_9$ .

Exercice 2 – suites du type Un=f(n)
Calculer les limites des suites suivantes :
a. $U_n=\frac{\sqrt{n}-1}{\sqrt{n}+1}$
b. $U_n=\frac{3n-4}{2n+1}$
c. $U_n=ln(1+\frac{1}{n})$
d. $U_n=cos(\frac{1}{n})$
e. $U_n=sin(n\frac{\pi}{3}$

Exercice 3 – théorème de comparaison
Calculer les limites des suites suivantes :
a. $U_n=1+\frac{sin n}{\sqrt{n}}$
b. $U_n=\frac{n+cos(\sqrt{n})}{\sqrt{n}}$

Exercice 4 – croissances comparées
Calculer les limites des suites suivantes en utilisant le théorème des croissances comparées.
a. $U_n=\frac{n^2}{2^n}$
b. $U_n=2^n-n^3$
c. $U_n=\frac{n}{ln(n^2+1)}$

Exercice 5 – croissances comparées
Etudier le sens de variation des suites suivantes :
a. $U_n=\frac{n}{n+1}$
b. $U_n=n-ln(1+n)$
c. $U_n=\frac{1\times 3\times .....\times (2n-1)}{2\times 4 \times ...... \times .... \times 2n}$

Exercice 6 – récurrence
Soit $(U_n) \,$ la suite définie par
$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,\,U_{n+1}=\sqrt{U_n+2}} \,.$
Démontrer par récurrence que :
$\red\fbox{\forall n \in\,\mathbb{N}\,,\,U_n<2 }\,$

Exercice 7 – récurrence
Soit $(U_n) \,.$ la suite définie par
$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,,\,U_{n+1}=2U_n-3} \,.$

Démontrer par récurrence que :
$\red\fbox{\forall n \in\,\mathbb{N}\,,\,U_n=3-2^n }\,.$

Exercice 8 – récurrence

On pose :
$\forall n \in\,\mathbb{N^*}\,,\,S_n=1^2+2^2+3^2+....+n^2=\sum_{k=1}^n k^2 \,.$
a. Calculer $S_1\,S_2\,,S_3\,,S_4 \,.$
b. Exprimer $S_{n+1}$ en fonction de $S_n$ .
c. Démontrer par récurrence que :
$\red\fbox{ \forall n \in\,\mathbb{N^*}\,\,S_n=\frac{n(n+1)(2n-1)}{6} }\,.$

Exercice 9 – Limite de suite numériques

Dans chacun des cas, étudier la limite de la suite proposée.
$a_n=\frac{5n^3+2n-4}{n^3+n^2+1}$
$b_n=\frac{2sinn+3}{n+1}$

$c_n=\frac{5^n-2^n}{5^n+2^n}$

Exercice 10 – Extrait du baccalauréat

Soient $(U_n)$ et $(V_n)$ les suites définies pour tout entier naturel n par :
$U_0=9\,,\,U_{n+1}=\frac{1}{2}U_n-3\,,\,V_n=U_n+6$
1.a. Montrer que $(V_n)$ est une suite géométrique à termes positifs .
b. Calculer la somme $S_n=\sum_{k=0}^{n}V_k$ en fonction de n et en déduire la somme $S'_n=\sum_{k=0}^{n}U_k$ en fonction de n .
c. déterminer $lim_{n \to +\infty} S_n$ et $lim_{n \to +\infty} S'_n$ .
2. On définit la suite $(W_n)$ par $W_n=ln V_n$ pour tout entier n .
Montrer que la suite $(W_n)$ est une suite arithmétique .
Calculer $S''_n=\sum_{k=0}^{n}W_k$ en fonction de n et déterminer $lim_{n \to +\infty} S''_n$
3. Calculer le produit $P_n=V_0\times V_1 \times ....\times V_n$ en fonction de n.
En déduire $lim_{n \to +\infty} P_n$ .

Exercice 11 – Quelques résultats historiques (R.O.C)

Démontrer que :
1.Toute suite convergente est bornée.
2.Toute suite croissante et non majorée diverge vers $+\infty$ .
3.Si une suite converge, alors sa limite est unique.
4.La suite de terme général $(-1)^n$ n’a pas de limite.
5. Si (un) est bornée et (vn) converge vers 0 alors (unvn) converge vers 0.
6.Toute suite convergente d’entiers relatifs est stationnaire et a pour limite un entier relatif.
7.Toute suite divergente vers $+\infty$ est minorée.

Exercice 12 – Moyenne arithmético-géométrique

Soient a et b deux réels tels que $a>b>0$ .
Soient $(a_n)$ et $(b_n)$ les suites définies par : $a_0=a;b_0=b$
$\forall n_in \mathbb{N},a_{n+1}=\frac{a-n+b_n}{2}$ et $b_{n+1}=\sqrt{a_nb_n}$ .
Démontrer que $(a_n)$ et $(b_n)$ convergent vers une même limite.

Divergence des suite (cos n) et (sin n)
Démontrer que les suites $(sin\,n)$ et $(cos\,n)$ divergent.

Exercice 13 – Comportement asymptotique des suites géométriques

1.Démontrer l’inégalité de Bernoulli :
pour tout réel x positif et tout entier naturel n, on a $(1+x)^n\geq 1+nx$ .
2.Soit (un) une suite définie par $u_n=a^n$ avec $a\in \mathbb{R}$ .

Démontrer que :

Si $a\in]1;+\infty[$ alors (un) est divergente vers $+\infty$ .
Si a=1 alors (un) est constante donc converge vers 1.
Si $a\in]-1;1[$ alors (un) est convergente vers 0.
Si $a\in]-\infty;-1[$ alors (un) n’a pas de limite.

Exercice 14 – Somme des cubes

Soit $n\in\mathbb{N}^*$ .
On désigne par $S_n$ la somme des cubes des n premiers entiers naturels impairs :
$S_n=1^3+3^3+5^3+...+(2n-1)^3$
Par exemple $S_3=1^3+3^3+5^3=153$ .
1.Démontrer, par récurrence, que pour tout entier positif non nul $S_n=2n^4-n^2$ .
2.Déterminer n tel que $1^3+3^3+5^3+...+(2n-1)^3=913\,276$ .

Exercice 15 – Notion de suite

Soient $(U_n)$ une suite croissante et majorée
et $(V_n)$ une suite décroissante et minorée.
Les suites $(U_n)$ et $(V_n)$ ont-elles nécessairement la même limite ?

Exercice 16 – Restitution organisée des connaissances (sujet type Bac )

On suppose connu le résultat suivant :
La suite $(U_n)$ tend vers $+\infty$ lorsque n tend vers $+\infty$ si tout
intervalle de la forme $]A;+\infty[$ contient toutes les valeurs de $U_n$
à partir d’un certain rang.
Soient $(U_n)$ et $(V_n)$ deux suites telles que :
* $U_n$ est inférieur ou égal à $V_n$ à partir d’un certain rang ;
* $U_n$ tend vers $+\infty$ lorsque n tend vers $+\infty$ .
Démontrer que la suite $(V_n)$ tend vers $+\infty$ lorsque n tend vers $+\infty$ .

Exercice 17 – Utilisation d’une suite auxiliaire arithmétique

Soit $(U_n)$ telle que $U_0=0$ et pour tout entier naturel n, $U_{n+1}=\frac{-4}{4+U_n}$ .
Soit $(V_n)$ telle que , pour tout entier naturel n, $V_{n }=\frac{1}{2+U_n}$ .
1. Démontrer que la suite $(V_n)$ est arithmétique de raison $\frac{1}{2}$ .
2. Exprimer $V_n$ en fonction de n et en déduire que pour tout entier naturel n,
$U_n=\frac{2}{n+1}-2$ .
3. Calculer la limite de la suite $(U_n)$ et celle de la suite $(V_n)$ .

Exercice 18 – Etude de la convergence d’une suite

Soit $(U_n)$ la suite définie par son premier terme $U_0=0$
et pour tout entier naturel n, $U_{n+1}=\frac{-4}{4+U_n}$ .
1. Démontrer par récurrence que pour tout entier naturel n, $-2<U_n\leq 0.$
2. Etudier le sens de variation de la suite $(U_n).$
3. Etudier la convergence de la suite $(U_n).$

Exercice 19 – Représentation graphique

On note (Un) la suite définie par $u_0=0$ et $u_{n+1}=u_n+2n-11$ .
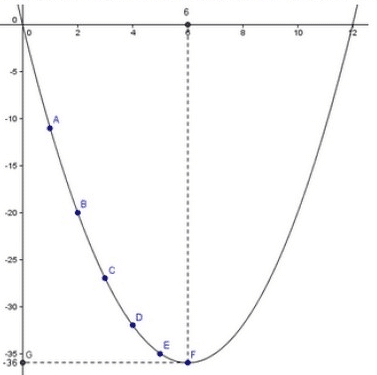
1.Calculer les six premiers termes de cette suite.
2.On a représenté ci-dessous les termes de la suite dans un repère et tracé une courbe qui passe par ces points.
Faire une conjecture sur l’expression de la fonction représentée par cette courbe puis sur l’expression de Un en fonction de n.
3.Démontrer la conjecture de la question précédente sur l’expression de Un en fonction de n.

Exercice 20 – étude d’une suite récurrente à l’aide d’une suite auxiliaire
Soit (Un) la suite définie par $\left\{\begin{matrix} u_0=9e\\u_{n+1} =3\sqrt{u_n} \end{matrix}\right.$ pour tout entier naturel n.
On pose $v_n=ln\left ( \frac{u_n}{9} \right )$ pour tout entier n.
1.Montrer que la suite ( $v_n$ ) est une suite géométrique dont on précisera la raison q et le premier terme $v_0$ .
2.Exprimer $v_n$ puis $u_n$ en fonction de n.
3.Etudier la limite de $u_n$ lorsque n tend vers $+\infty$ .

Exercice 21 : étude d’une suite récurrente linéaire d’ordre 2.

Considérons la suite (Un) définie pour tout entier n par $\left\{\begin{matrix} u_{n+2}=5u_{n+1}-6u_n\\ u_0=1 \\ u_1=2 \end{matrix}\right.$ .
Démontrer que pour tout entier n : $u_n=2^n$ .

Exercice 22 – série harmonique alternée
Soit (Sn) la suite définie pour tout n non nul par : $S_n=\sum_{p=1}^{n}\frac{(-1)^{p-1}}{p}$ .
Le but de cet exercice est de démontrer que la suite (Sn) converge vers ln2.
1.Calculer $S_1, S_2, S_3\, et\, S_4$ ..
2.On considère les suites (Un) et (Vn) définies par : $u_n=S_{2n}$ et $v_n=S_{2n+1}$ .
Démontrer que ces deux suites sont adjacentes.

Exercice 23 :

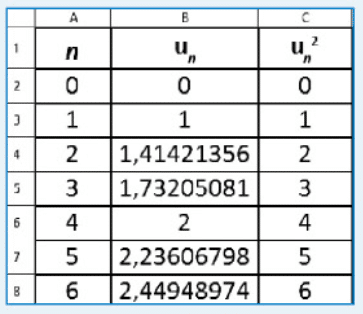
u est la suite définie par $u_0=0$ et, pour tout nombre entier naturel n, $u_{n+1}=\sqrt{u_n^2+1}$ .

Avec le tableur, on a obtenu ci-dessous les premières valeurs de $u_n$ et $u_n^2$ .

Conjecturer une expression de $u_n$ en fonction de n.
Valider cette conjecture par un raisonnement par récurrence.

Exercice 24 :

V est la suite définie par $V_0=0$ et pour tout nombre entier naturel n, $V_{n+1}=V_n+2n+2$ .

Démontrer par récurrence que pour tout nombre entier naturel n, $V_n=n(n+1)$ .

Exercice 25 :

Montrer par récurrence que, pour tout entier naturel n, $2^n\geq \, n+1$ .

Exercice 26 :

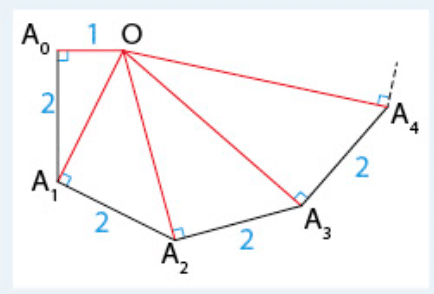
Sur cette figure :

$OA_0=1$
$A_0A_1=A_1A_2=...=2$
les triangles $OA_0A_1,OA_1A_2,...$ sont rectangles.

Démontrer par récurrence, que pour tout nombre entier naturel n, $OA_n=\sqrt{4n+1}$ .

Exercice 27 :

Etudier, en justifiant, la limite en l’infini de chacune des suites numériques suivantes :

$1.\,u_n=3(2-0,9^n)\\2.\,v_n=1,01^n-5\\3.\,w_n=\frac{3+0,2^n}{0,9^n-5}\\4.\,t_n=\frac{4^n+5}{2\times 3^n}$

Exercice 28 :

u est la suite géométrique de raison 0,8 et de premier terme $u_1=-3$ .

Pour tout nombre entier naturel n non nul, exprimer $S_n=u_1+u_2+u_3+...+u_n$ en fonction de n.
Etudier la limite de la suite $\left ( S_n \right )$ .

Exercice 29 :

On considère la suite $(u_n)$ définie par $u_0=0,7$ et pour tout $n\in \mathbb{N}$ ,

$u_{n+1}=\frac{3u_n}{1+2u_n}$ .

1)Soit f la fonction définie sur $[0;+\infty[$ par $f(x)=\frac{3x}{1+2x}$ .

a)Etudier les variations de f sur $[0;+\infty[$ .

b) En déduire que si $x\in[0;1]$ , alors f ‘ (x) $\in[0;1]$ .

2)Démontrer par récurrence que, pour tout entier naturel n, $0\leq u_n\leq 1$ .

3)Déterminer le sens de variation de la suite $(u_n)$ .

Exercice 30 :

La suite $(u_n)$ est définie par $u_1=1$ et pour tout $n\in \mathbb{N}^*$ ,

$u_{n+1}=u_n+2n+1$ .

1)A l’aide de la calculatrice ou d’un tableur, déterminer les dix premiers

termes de la suite $(u_n)$ .

2)a)Quelle conjecture peut-on faire sur l’expression de $u_n$ en fonction de n ?

b)Démontrer cette conjecture par récurrence.

Exercice 31 :

Montrer par récurrence que, pour tout entier naturel n non nul,

$\sum_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

Exercice 32 :

Déterminer la limite de $(u_n)$ définie sur $\mathbb{N}^*$ en utilisant les théorèmes généraux.

$1)u_n=(1-2n)(n^2+3)$ .

$2)u_n=\frac{3}{3+2n}$ .

$3)u_n=4n-1+\frac{5}{\sqrt{n}}$ .

$4)u_n=-n^2-5n+\frac{1}{n}$

Exercice 33 :

Soit la suite $(u_n)$ définie par $u_0=5$ et, pour tout $n\in \mathbb{N}$ ,

$u_{n+1}=-\frac{1}{3}u_n+1$ .

Soit $(v_n)$ la suite définie pour tout entier naturel n par :

$v_n=4u_n-3$ .

1)Montrer que la suite $(v_n)$ est géométrique de raison $-\frac{1}{3}$ .

Préciser le premier terme.

2) Déterminer l’expression de $v_n$ en fonction de n et en déduire que,

pour tout entier naturel n :

$u_n=\frac{17}{4}\times (-\frac{1}{3})^n+\frac{3}{4}$ .

3) Déterminer la limite de la suite $(u_n)$ .

Exercice 34 :

Etudier si les suites suivantes, définies sur $\mathbb{N}$ , sont bornées.

$1)u_n=(\frac{1}{3})^n-8$ .

$2)u_n=5sin(5n+1)-3$ .

$3)u_n=cos(n^2)-n$ .

Exercice 35 :

$(u_n )$ est la suite définie sur $\mathbb{N}$ par : $u_n=4n^2-8n+1$

On se propose d’étudier la limite de la suite $(u_n )$ de trois façons différentes.
a) Démontrer que pour tout n, $u_n=4(n-1)^2-3$
b) En déduire la limite de la suite $(u_n )$ .
2. Pour tout $n\geq 1$ , mettre $4n^2$ en facteur dans l’expression de $u_n$ et conclure pour la limite de (un).
3. a) Démontrer que pour tout $n \geq 4$ , $u_n \geq 2n^2$
b) En déduire la limite de la suite $(u_n )$ .

Exercice 36 :

Jenny a ouvert un livret A et a déposé 5 000 €.

Les intérêts composés sont de 0,5 % par an et, en chaque fin d’année, Jenny ajoutera 100 € sur son livret.
On désigne par $J_n$ la somme, en euro, sur son livret A après n années, avec $n \in \mathbb{N}$ .
a) Démontrer que, pour tout n, $Jn \geq 5 000 + 1 00n$ .
b) En déduire la limite de la suite ( $J_n$ ).
c) Tabuler la suite ( $J_n$ ) l’écran de la calculatrice et déterminer après combien d’années Jenny disposera de plus de 7 OOO €.

Exercice 37 :

$(u_n )$ est la suite définie par $u_0 > 0$ et pour tout entier naturel n, $u_{n+1}=u_n+\frac{1}{u_n}$ .
Trois amis émettent des conjectures.
Cyril affirme : « Tous les termes de la suite sont strictement positifs ».
Magali affirme : « La suite $(u_n )$ diverge vers $+\infty$ quelle que soit la valeur du premier terme $u_0$ ».
Olivier rétorque : « La suite $(u_n )$ peut converger si on choisit $u_0$ ni trop grand ni trop proche de 0 ».
a) L’affirmation de Cyril est-elle vraie ? Justifier.
b) Démontrer par récurrence que pour tout entier naturel n, $u_n^2\geq 2n$ .
c) L’une des affirmations de Magali et d’Olivier est-elle vraie ? Justifier.

4.4/5 - (23125 votes)

Suites : exercices de maths en terminale corrigés en PDF.

Suites numériques : exercices de maths en terminale corrigés en PDF.

Produit scalaire : exercices de maths en terminale corrigés en PDF.

Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.

Représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.