Exercice 1 – Arithmétique en terminale

1-Etablir que pour tout
2-Montrer que pour tout 

Exercice 2 – Démontrer qu’un entier est divisible par 3

n designe un nombre entier naturel.
Demontrer que n(n+2)(n+4) est divisible par 3.

Exercice 3 – Démontrer la propriété suivante :

Soit a et b deux entiers naturels non nuls, alors on a :
PGCD(a ;b)×PPCM(a ;b) = a × b.

On admettra la propriété suivante :

Si a’ et b’ sont deux entiers naturels premiers entre eux alors PPCM(a’ ;b’) = a’×b’.

Exercice 4 – Système d’équations
Résoudre dans  , le système :

Exercice 5 – Montrer qu’un entier n’est jamais un nombre premier

On désigne par a et b deux entiers naturels supérieurs ou égaux à 2.
1) Développer le carré .
2) En déduire que l’entier naturel  n’est jamais un nombre premier.

Exercice 6 – Congruences

Exercice 7 – Différence de cube
1. Démontrer que pour tout  et  ,on a  .
2. résoudre l’équation   où les inconnues sont des entiers naturels .

Exercice 8 – Théorème de la division euclidienne dans Z
On note  .
D’après le théorème de la divison euclidienne dans ,
il existe  et  tels que :
.
Démontrer que le couple (q,r) est unique .

Exercice 9 – Problème sur les racines carrées
On note   tel que n soit le carré d’aucun entier.
Rappel : tout entier naturel admet une décomposition unique en produit de facteurs premiers .
On suppose que  et donc qu’il existe  et 
tels que  avec pgcd(p,q)=1.
1. Exprimer  en fonction de  et  .
2. Que peut-on dire des exposants des facteurs premiers figurant dans la décomposition de  ?
3. Conclure .
4. Démontrer par l’absurde que  .

Exercice 10 – Somme à calculer
On note .
Démontrer que pour tout  , on a :
 .

Exercice 11 – Calcul d’une somme
Démontrer par récurrence que pour tout  ,
on a  .

Exercice 12 – Puissance, arithmétique et raisonnement par récurrence
On note x un réel positif .
Démontrer par récurrence que pour tout entier  , on a   .

Exercice 13 – Contraposée et raisonnement par récurrence
On note  .
Le but de cet exercice est de montrer par contraposition la propriété suivante :
Si l’entier  n’est pas divisible par 8 alors l’entier n est pair .
1. Ecrire la contraposée de la proposition précédente .
2. En remarquant qu’un entier impair n s’écrit sous la forme 
avec  et  ( à justifier).Prouver la contraposée .
3. Que peut-on en déduire ?

Exercice 14 – Multiple d’un nombre
Montrer que, pour tout entier ,  est un multiple de 3 .

Exercice 15 -Raisonnement par récurrence
1. Développer, réduire et ordonner .
2. En déduire que pour tout entier  ,  est un multpile de 5 .

Exercice 16 -Somme des cubes
1. Montrer que  .
2. En déduire la valeur de  .

Exercice 17 -Multiple d’un nombre
Montrer que pour tout entier   est un multiple de 3.

Exercice 18 -Bac s spécialité et arithmétique
Soit n un entier naturel .
1. trouver suivant les valeurs de n, les restes de la division de par 13 .
2. En déduire que est divisible par 13.
3. Démontrer que, pour tout entier naturel n supérieur ou égal à 1, le nombre est divisible par 13 .

Exercice 19 – Problème sur l’arithmétique

Soit n un entier relatif et 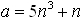. Montrer que a est divisible par 3.

Exercice 20
Soit n un entier naturel
Montrer que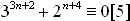

Exercice 21
Soit p un nombre entier naturel impair. Montrer que la somme de p entiers naturels consécutifs est un multiple de p.

Exercice 22
Indice : Théorème de Bézout
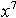
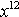
Soit x un réel. Montrer que si et sont des nombres rationnels, alors x l’est également.

Exercice 23
Indice: Lemme de Gauss
Résoudre dans N* l’équation :

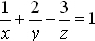
Exercice 24
Soit n un entier naturel

Exercice 25 – Nombres de Mersenne
Soit n un entier naturel non nul.
On considère les nombre de la forme : 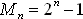dits nombres de Mersenne.
1. Montrer que 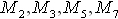sont des nombres premiers.
2. Montrer que si p est un diviseur de n, alors est divisible par .
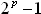
En déduire que si est un nombre premier alors n l’est également.
3. Etudier la réciproque.

Exercice 26
Trouver tous les couples (a,b) d’entiers naturels vérifiant : ppcm(a,b) = 40 et a+b=60

Exercice 27
Soit a et b deux entiers naturels.
Montrer que si pgcd(a,b) = 1 alors pgcd(a,b²) = 1

Exercice 28
Soit n un entier naturel impair,
Montrer que parmi (n-1)²+1 entiers, il en existe n dont la somme est un multiple de n.

Exercice 29
Soit n un entier naturel
1. Démontrer que n²+5n+4 et n²+3n+2 sont divisibles par (n+1)
2. Déterminer l’ensemble des valeurs de n pour lesquelles 3n²+15n+19 est divisible par n+1
3. En déduire que pour tout entier naturel n, 3n²+15n+19 n’est pas divisible par n²+3n+2.

Exercice 30 – Nombres de Fermat .
Soit n un entier naturel .
a. Montrer que si est premier, alors n est une puissance de 2
b. On pose (nombres de Fermat). Montrer que les sont deux à deux premiers entre eux.