Fonction exponentielle : corrigé des exercices en terminale en PDF.

🔍Corrigés Détaillés

1ere • Scolaire

Fonction exponentielle

🔎 Analyse : 20 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Primitive d’une fonction composée. Exercices corrigés de mathématiques en Terminale S sur les fonction exponentielles.

Exercice 1 :

Soit la fonction f définie par $f(x) = (x - 3)^{\frac{2}{3}}$

1. Donner le domaine de définition de la fonction f.

nous avons $f(x)=e^{\frac{2}{3}ln(x-3)}$

donc pour que f soit définie, il faut que x-3>0 soit x>3.

ainsi :

${\color{DarkRed} D_f=]3;+\infty[}$

2. Donner une primitive de la fonction.

les primitives de f sont de la forme :

$F(x)=\frac{3}{5}(x-3)^{\frac{2}{3}+1}+k=\frac{3}{5}(x-3)^{\frac{5}{3} }+k\,,\,k\in\mathbb{R}$

Exercice 2 :

soit la fonction f tel que : $f(x)=x^x +1$

1. Indiquer le domaine de définition de f et transformer l’écriture du réel f(x).

$f(x)=e^{xlnx}+1$

donc $D_f=]0;+\infty[$

2. Donner un prolongement par continuité de f au point 0.

$f(0)=2$

3. Etudier la dérivabilité de f au point 0.

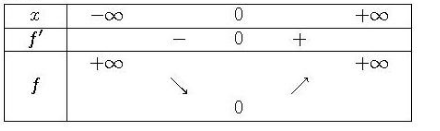
4. Calculer la dérivée de f et étudier son signe. Etablir le tableau de variations.

5. Décrire comment se présente la tangente en ce point.

6. Construire la courbe dans un repère approprié.

Exercice 3 :

1. Démontrer que pour tout réel x, $e^{-x}=\frac{1}{e^x}$ .

d’après la formule ci-dessus :

$e^{x+(-x))}=e^xe^{-x}$

donc

$e^{0}=e^xe^{-x}$

$1=e^xe^{-x}$

$\frac{1}{e^x}=e^{-x}$ car $e^x>0$

2. Démontrer que pour tout réel x et pour tout entier naturel n,

$(e^{x})^n=e^{nx}$

Exercice 4:

Résoudre les inéquations suivantes :

1. $x^{\pi}<\frac{1}{2}.$

La fonction logarithme népérien est strictement croissante sur $\mathbb{R}$ .

$ln(x^{\pi})<ln(\frac{1}{2})$

${\pi}lnx^<-ln(2)$

$lnx^<\frac{-ln(2)}{\pi}$

$e^{lnx}<e^(\frac{-ln(2)}{\pi})$

${\color{DarkRed} x<e^(\frac{-ln(2)}{\pi})}$

2. $3^x\geq 4.$

$ln(3^x)\geq ln4$

$ln(3)x\geq ln4$

$x\geq \frac{ln4}{ln3}$ ( car ln 3 > 0)

Exercice 5 :

Déterminer les primitives des fonctions suivantes :

1. $f(x)=sinx\times e^{cosx}$ .

une primitive est de la forme $F(x)=-e^{cosx}+k\,(k\in\mathbb{R})$ .

2. $f(x)=x^{-2}e^{\frac{1}{x}}\,sur\,]-\infty;0[.$

une primitive est de la forme $F(x)=-e^{\frac{1}{x}}+k\,(k\in\mathbb{R})$ .

Exercice 6 :

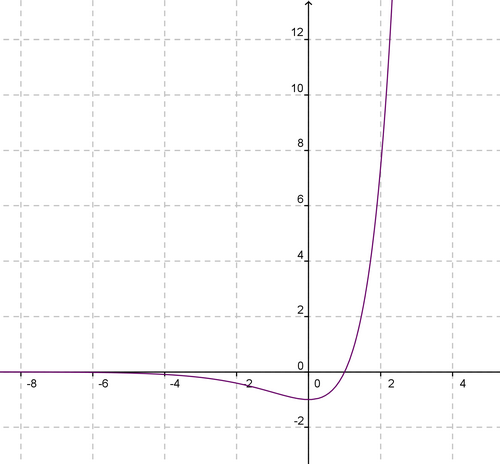
Soit $f(x)=(x-1)e^x$ pour x ∈ R.

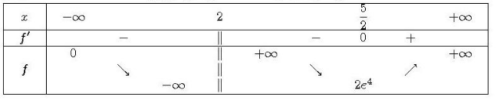
1. Déterminez les limites de f aux bornes du domaine de définition.

$\lim_{x \mapsto -\infty }f(x)=0$ et $\lim_{x \mapsto +\infty }f(x)=+\infty$

2. Etudiez les variations de f.

$f'(x)=1\times e^x+(x-1)e^x=xe^x$

$f'\geq 0$ sur $[0;+\infty[$ donc f est croissante sur $[0;+\infty[$ .

3. Construisez la courbe C représentant f.

Exercice 7 :

Résoudre les équations et inéquations proposées.

$1.e^{2x^2+3}=e^{7x}\\ln(e^{2x^2+3})=ln(e^{7x})\\2x^2+3=7x$

$2x^2-7x+3=0$

Calculons la valeur du discriminant :

$\Delta =(-7)^2-4\times 2\times 3=49-24=25>0$

Le discriminant est strictement positif, il existe donc deux racines réelles distinctes.

$x_1=\frac{7+5}{4}\,et\,x_2=\frac{7-5}{4}$

$x_1=3\,et\,x_2=\frac{1}{2}$

Exercice 8 :

1.a) Pour calculer la dérivée de $C_u(x)$ , on utilise la formule pour la dérivée d’un quotient :

$C^{'}_{u(x)} = \frac{d}{dx}[x-10]+\frac{d}{dx}\left(\frac{900}{x}\right) = 1 - \frac{900}{x^2}$

En simplifiant, on obtient :

$C^{'}_{u(x)} = \frac{x^2-900}{x^2} = \frac{(x-30)(x+30)}{x^2}$

b) Le dénominateur est toujours positif car x est dans l’intervalle [10, 100].

Le numérateur est positif pour x > 30 et négatif pour x < 30.

Donc, le signe de $C^{'}_{u(x)}$ dépend du signe de (x-30)(x+30). On peut établir le tableau de signes suivant :

x | 10 | 30 | 100
—-|—–|—–|—–
$C^{'}_{u(x)}$ | – | 0 | +

En utilisant ce tableau, on peut établir le tableau de variation de $C_{u(x)}$ :

x | 10 | 30 | 100
—-|—–|—–|—–
$C_{u(x)}$ | + | mín | +

c) Le coût unitaire est le plus bas lorsque $C_{u(x)}$ est minimal.

Comme la fonction $C_{u(x)}$ est décroissante sur [10,30] et croissante sur [30,100], son minimum est atteint en x = 30. Le coût unitaire minimal est donc $C_{u(30)} = 20$ .

Le bénéfice de l’entreprise par objet vendu est la différence entre le prix de vente et le coût unitaire, soit :

$B_0 = 100 - 20 = 80$

2. Le bénéfice global de l’entreprise est donné par la formule $B(x) = x(100-C_u(x))$ , car l’entreprise fabrique et vend x objets par jour.

En remplaçant $C_u(x)$ par son expression en fonction de x, on obtient :

$B(x) = x(100 - (x-10+\frac{900}{x})) = -x^2+110x - 900$

3. Pour trouver le maximum de la fonction B sur [10,100], on peut calculer sa dérivée :

$B^{'}(x) = -2x + 110$

La dérivée est nulle en x = 55, ce qui est bien dans l’intervalle [10,100]. Pour déterminer que cette valeur est un maximum, on peut regarder le signe de la dérivée dans les intervalles [10,55] et [55,100]. On peut établir le tableau de signes suivant :

x | 10 | 55 | 100
—-|—–|—–|—–
B^'(x) | – | + | –

Donc, la fonction B est décroissante sur [10,55] et croissante sur [55,100], avec un maximum en x = 55. Le bénéfice maximal est donc $B(55) = -55^2+110 \times 55-900 = 3025$ .

Exercice 9 :

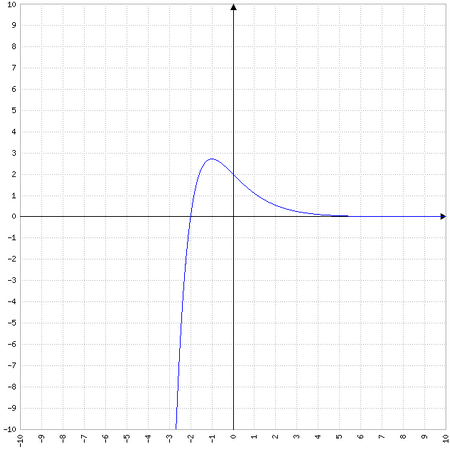
La courbe représente une fonction f définie par $f(x)= (ax+b)exp(-x)$ .

Elle passe par les points de coordonnées (o;2) et (-2;0).

1) Calculer a et b .

$f(0)=2\,et\,f(-2)=0$

$be^0=2\,et\,(-2a+b)e^{2}=0$

$b=2\,et\,(-2a+2)e^{2}=0$

$b=2\,et\,-2a+2=0$

$b=2\,et\,a=1$

Conclusion : $f(x)=(x+2)e^{-x}$

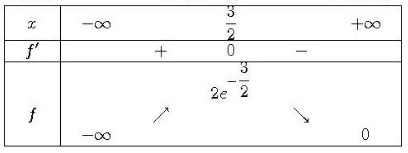
2) Déterminer les coordonnées du maximum après avoir étudié les variations de f.

f est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables sur cet intervalle .

$f'(x)=e^{-x}+(x+2)\times (-e^{-x})$

$f'(x)=e^{-x}-xe^{-x}-2e^{-x}$

$f'(x)=-xe^{-x}-e^{-x}$

$f'(x)=-(x+1)e^{-x}$

Le signe de f ‘ est celui de -x-1 puisque l’exponentielle est strictement positive sur R .

$-x-1\geq 0$

$x\leq -1$

Conclusion : f est croissante sur $]-\infty;-1]$ .

Exercice 10 :

Simplifier au maximum :

$A=ln(\sqrt{80})-\frac{1}{2}ln5$

$A=ln(80^{\frac{1}{2}})-\frac{1}{2}ln5$

$A=\frac{1}{2}ln(80)-\frac{1}{2}ln5$

$A=\frac{1}{2}ln(5\times 16)-\frac{1}{2}ln5$

$A=\frac{1}{2}ln5+\frac{1}{2}ln16-\frac{1}{2}ln5$

$A=\frac{1}{2}ln16$

$A=\frac{1}{2}ln2^4$

$A=\frac{4}{2}ln2$

${\color{DarkRed} A=2ln2}$

$B=ln(\sqrt{6}-1)+ln(\sqrt{6}+1)-ln(\sqrt{100})-ln\frac{1}{8}$

$B=ln[(\sqrt{6}-1)(\sqrt{6}+1)]-ln(100^{\frac{^1}{2}})-(-ln8) )$

$B=ln[(\sqrt{6})^2-1^2]-\frac{1}{2}ln(100)-(-ln8 )$

$B=ln5-\frac{1}{2}ln(10^2)+ln8$

$B=ln5-\frac{2}{2}ln(10)+ln8$

$B=ln5-ln(10)+ln8$

$B=ln5-ln(5\times 2)+ln2^3$

$B=ln5-ln5-ln 2+3ln2$

${\color{DarkRed} B=2ln2}$

Exercice 11 :

$1.f(x)=e^{4x+1}\\f'(x)=4e^{4x+1}\\ \\2.f(x)=e^x+x^2+1\\f'(x)=e^x+2x\\3.f(x)=5e^x+5xe^x\\f'(x)=5e^x+5e^x+5xe^x=10e^x+5xe^x\\4.f(x)=\frac{e^x+1}{e^x-1}\\f'(x)=\frac{e^x(e^x-1)-(e^x+1)e^x}{(e^x-1)^2}=\frac{e^{2x}-e^x-e^{2x}-e^x}{(e^x-1)^2}=\frac{-2e^x}{(e^x-1)^2}\\5.f(x)=\frac{3x+1-e^x}{e^x}\\f'(x)=\frac{(3-e^x)e^x-(3x+1-e^x)e^x}{e^{2x}}\\=\frac{3e^x-e^{2x}-3xe^x+1e^x-e^{2x}}{e^{2x}}\\6.f(x)=x^3e^{-x}\\f'(x)=3x^2e^{-x}-x^3e^{-x}=(3x^2-x^3)e^{-x}$

Exercice 12 :

$1. e^xe^{-x.}=e^{x-x}=e^0=1\\2.e^xe^{-x+1}=e^1=e\\3.ee^{-x}=e^1e^{-x}=e^{1-x}\\4.(e^{-x})^2=e^{-2x}\\5.\frac{e^2x}{e^{2-x}}=e^{2x-2+x}=e^{3x-2}\\6.\frac{(e^x)^3}{e^{2x}}=e^{3x-2x}=e^x$

Exercice 13 :

1. On peut remarquer que l’équation peut être mise sous la forme d’une équation du second degré en $e^x$ en posant $e^x = t$ :

$t^2 + 3t - 4 = 0$

On peut résoudre cette équation en utilisant la méthode habituelle pour résoudre une équation quadratique :

$(t+4)(t-1) = 0$

Donc, $t = -4$ ou $t = 1$ . En remplaçant $t$ par $e^x$ , on trouve que les solutions de l’équation sont :

$e^x = -4$ (pas de solution réelle) ou $e^x = 1 \iff x=0$

2. On factorise par $e^x$ :

$e^x(e^{2x-1} - 1) = 0$

Donc, $e^x = 0$ (pas de solution réelle) ou $e^{2x-1} = 1 \iff 2x-1=0 \iff x=\frac{1}{2}$

3. On peut remarquer que l’équation est similaire à $\cosh x = \frac{e^x + e^{-x}}{2} = \frac{1}{2}$ , qui est équivalente à $\cosh^{-1}{\frac{1}{2}} = x$ .

En utilisant la définition de la fonction cosinus hyperbolique inverse (aussi appelée arccosh), on a :

$x = \ln\left(\frac{1}{2} + \sqrt{\frac{1}{4}-1}\right) = \ln\left(\frac{1}{2} + \frac{i\sqrt{3}}{2}\right) = \ln\left(e^{\frac{i\pi}{3}}\right) = \frac{i\pi}{3}$

$x = \ln\left(\frac{1}{2} - \sqrt{\frac{1}{4}-1}\right) = \ln\left(\frac{1}{2} - \frac{i\sqrt{3}}{2}\right) = \ln\left(e^{-\frac{i\pi}{3}}\right) = -\frac{i\pi}{3}$

donc les solutions de l’équation sont $x = \pm\frac{i\pi}{3}$ .

4. On peut diviser les deux membres de l’inéquation par $e^x$ pour obtenir :

$e^x + e^{-x} < 1$

En utilisant la même astuce que précédemment, on remarque que cette inéquation équivaut à $\cosh x < \frac{1}{2}$ .

Or, on sait que $\cosh x \geq 1$ pour tout $x \in \mathbb{R}$ , donc il n’y a pas de solution à cette inéquation.

5. On peut réécrire l’inéquation sous la forme $e^{2x} < \frac{3}{4}(e^x)^2 + \frac{1}{4}$ , ce qui peut être factorisé en $(e^x - \frac{1}{2})(3e^x + 1) < 0$ .

On peut résoudre cette inéquation en utilisant le tableau de signes suivant :

$x$ | $-\infty$ | $\frac{\ln 3}{2}$ | $+\infty$
— | — | — | —
$e^x-\frac{1}{2}$ | $-$ | $-$ | $+$
$3e^x + 1$ | $-$ | $+$ | $+$
Produit | $+$ | $-$ | $+$

Donc, les solutions sont $x \in \left(-\infty, \frac{\ln 3}{2}\right)$ .

6. On peut appliquer la fonction exponentielle des deux côtés de l’inéquation, en prenant soin de conserver le sens de l’inégalité :

$e^{x\left(\frac{2x-1}{3x+1}\right)} > e^{-2}$

En utilisant la propriété de la fonction exponentielle $a^b > c \iff b\ln a > \ln c$ , on peut appliquer le logarithme naturel des deux côtés de l’inégalité :

$x\left(\frac{2x-1}{3x+1}\right) > -2$

En multipliant par le dénominateur $3x+1$ (qui est toujours positif puisque $x > 0$ ), on obtient :

$2x^2 - 7x - 2 > 0$

On peut résoudre cette inéquation en utilisant la méthode habituelle pour résoudre une inéquation quadratique :

$x < \frac{1}{2}$ ou $x > 2$

Mais on doit également vérifier que le dénominateur de la fraction initiale est toujours positif dans l’intervalle des solutions (c’est-à-dire $x \in (0, \infty)$ ),

sinon nous aurions une solution qui ne fonctionne pas.

Le dénominateur $3x+1$ est toujours positif dans cet intervalle, donc l’ensemble des solutions de l’inéquation initiale est $x \in \left(0, \frac{1}{2}\right) \cup (2, \infty)$ .

tableau de variations

Exercice 14 :

Exercice 15 :

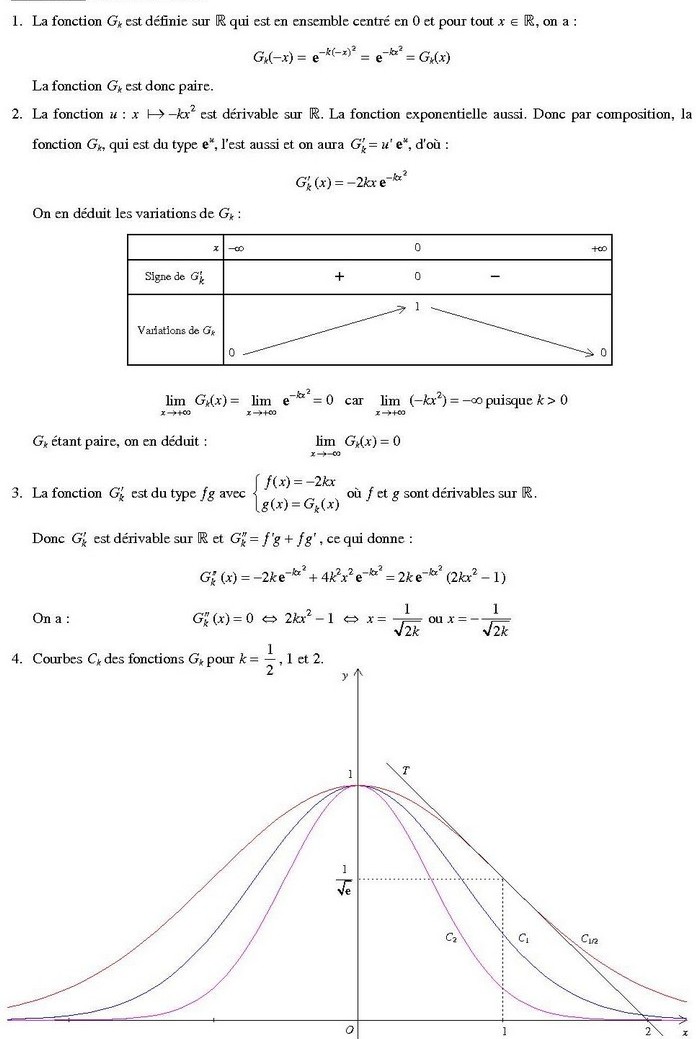
1. Pour tout $x \in \mathbb{R}$ , on a :

$G_k(-x) = e^{-k(-x)^2} = e^{-kx^2} = G_k(x)$

Donc, la fonction $G_k$ est paire.

2. La fonction $G_k$ est bien dérivable sur $\mathbb{R}$ car elle est la composée de fonctions dérivables. Pour tout $x \in \mathbb{R}$ , on a :

$G'_k(x) = (-2kx)e^{-kx^2} = -2kxG_k(x)$

En utilisant le signe de $G_k$ et le tableau de variations de $x \mapsto x$ , on peut établir le tableau de variation de $G_k$ :

x |-\infty | 0 |\infty
———|————–|——–|——
G_k(x) |+\infty reste | 1 |+\infty reste
G’_k(x) | – | 0 |+

3. Pour résoudre $G'_k(x) = 0$ , on doit chercher les valeurs de $x$ pour lesquelles $-2kxG_k(x) = 0$ . Cette équation est vraie si et seulement si $x = 0$ ou $G_k(x) = 0$ . La valeur $x = 0$ n’est pas une solution car ce point correspond à un maximum local de la fonction $G_k$ . Donc, les solutions doivent vérifier $G_k(x) = 0$ , c’est-à-dire $e^{-kx^2} = 0$ . Mais cette équation n’a pas de solution réelle car l’exponentielle est toujours strictement positive.

4. Voici les courbes de $G_k$ pour $k = \frac{1}{2}, 1, 2$ :

![Courbes_Gk.png](attachment:Courbes_Gk.png)

5. Pour tout $x \in \mathbb{R}$ et pour tout $h < k > 0$ , on a :

$G_h(x) = e^{-hx^2} \leq e^{-kx^2} = G_k(x)$

Cela s’explique par le fait que le coefficient $-hx^2$ est plus petit (ou égal) que le coefficient $-kx^2$ , donc l’exponentielle décroît moins rapidement pour $h$ que pour $k$ , ce qui fait que la fonction $G_h$ est plus grande (ou égale) que la fonction $G_k$ pour tout $x \in \mathbb{R}$ .

6. L’équation $G''_{\frac{1}{2}}(x) = 0$ équivaut à $4x^2 - 2 = 0$ , qui a pour solution positive $\alpha = \frac{1}{\sqrt{2}}$ .

7. La tangente à la courbe de $G_{\frac{1}{2}}$ au point d’abscisse $\alpha$ est la droite affine de coefficient directeur $G'_{\frac{1}{2}}(\alpha) = -\sqrt{2}\,G_{\frac{1}{2}}(\alpha)$ et passant par le point $(\alpha, G_{\frac{1}{2}}(\alpha))$ . On a donc :

$y - G_{\frac{1}{2}}(\alpha) = -\sqrt{2}\,G_{\frac{1}{2}}(\alpha)(x-\alpha)$

soit :

$y = -\sqrt{2}\,G_{\frac{1}{2}}(\alpha)(x-\alpha) + G_{\frac{1}{2}}(\alpha)$

8. Voici le graphique de la fonction $G_{\frac{1}{2}}$ ainsi que de sa tangente en $\alpha = \frac{1}{\sqrt{2}}$ :

Exercice 16 :

Partie A

1a. Soit $g$ une fonction définie et dérivable sur $\mathbb{R}$ telle que $g(x) = h(x)e^{-x}$ pour tout $x \in \mathbb{R}$ . En dérivant cette égalité par rapport à $x$ , on a :

$g'(x) = h'(x)e^{-x} - h(x)e^{-x}$

Pour que $g$ soit solution de l’équation différentielle $(E_n)$ donnée, il faut que $g'(x) + g(x) = \frac{x^n}{n!}e^{-x}$ pour tout $x \in \mathbb{R}$ . En utilisant l’expression de $g$ en fonction de $h$ , on a :

$g'(x) + g(x) = h'(x)e^{-x} - h(x)e^{-x} + h(x)e^{-x} = h'(x)e^{-x}$

Donc $g$ est solution de $(E_n)$ si et seulement si $h'(x) = \frac{x^n}{n!}$ pour tout $x \in \mathbb{R}$ .

1b. En intégrant $h'(x) = \frac{x^n}{n!}$ par rapport à $x$ , on obtient :

$h(x) = \frac{1}{n!}\int_0^x t^n dt = \frac{x^{n+1}}{(n+1)!}$

D’après la question précédente, la fonction $g$ correspondante est donnée par :

$g(x) = \frac{x^{n+1}}{(n+1)!}e^{-x}$

2a. Soit $\phi$ une fonction définie et dérivable sur $\mathbb{R}$ . Alors $\phi$ est solution de $(E_n)$ si et seulement si $\phi - g$ est solution de l’équation différentielle $y'(x) + y(x) = 0$ . En effet, en substituant $\phi - g$ à $y$ dans l’équation $(E_n)$ , on obtient :

$(\phi-g)'(x) + (\phi-g)(x) = \phi'(x)e^{-x} - \frac{x^{n+1}}{(n+1)!}e^{-x} + \frac{x^{n+1}}{(n+1)!}e^{-x} - \phi(x)e^{-x} = (\phi'(x) - \frac{x^{n}}{n!})e^{-x}$

Pour que $\phi$ soit solution de $(E_n)$ , il faut et il suffit que $(\phi'(x) - \frac{x^{n}}{n!})e^{-x} = 0$ pour tout $x \in \mathbb{R}$ , c’est-à-dire que $\phi'(x) = \frac{x^{n}}{n!}$ pour tout $x \in \mathbb{R}$ . On obtient ainsi que $\phi - g$ est solution de $y'(x) + y(x) = 0$ .

2b. L’équation $y'(x) + y(x) = 0$ est une équation différentielle linéaire d’ordre 1 à coefficients constants. Sa solution générale est donnée par $y(x) = Ce^{-x}$ pour une constante $C$ fixée en fonction des conditions initiales. Ici, on cherche à résoudre $y'(x) + y(x) = 0$ avec la condition initiale $y(0) = 0$ . En substituant $y(x) = Ce^{-x}$ dans cette condition initiale, on obtient $C = 0$ , donc la solution de cette équation avec cette condition initiale est $y(x) = 0$ .

2c. Pour tout entier $n \geq 1$ , notons $\phi_n$ la solution de $(E_n)$ avec la condition initiale $\phi_n(0) = 0$ . On peut écrire :

$\phi_{n+1}(x) - g(x) = (\phi_n(x) - g(x))' = -(\phi_n(x) - g(x))$

donc $\phi_{n+1}(x) - g(x) = Ce^{-x}$ pour une certaine constante $C$ . En utilisant la condition initiale $\phi_{n+1}(0) = 0$ , on a $C = -\frac{1}{(n+1)!}$ , donc :

$\phi_{n+1}(x) = \frac{x^{n+1}}{(n+1)!}e^{-x} - \frac{1}{(n+1)!}e^{-x} = \frac{x^{n+1} - 1}{(n+1)!}e^{-x}$

Ainsi, pour tout $n \geq 1$ , la solution de $(E_n)$ avec la condition initiale $\phi_n(0) = 0$ est donnée par :

$\phi_n(x) = \frac{x^n}{n!}e^{-x}$

2d. En particulier, la solution de $(E_0)$ avec la condition initiale $\phi_0(0) = 0$ est donnée par $\phi_0(x) = e^{-x}$ , donc d’après la question précédente, la solution de $(E_n)$ avec la condition initiale $\phi_n(0) = 0$ est donnée par $\phi_n(x) = \frac{x^n}{n!}e^{-x}$ pour tout $n \geq 0$ .

Partie B

1a. On a :

$f_0(x) = e^{-x}$

$f_1(x) = xe^{-x}$

et $f_1'(x) + f_1(x) = e^{-x}$ , donc $f_1$ est solution de $y'(x) + y(x) = f_0(x)$ .

Soit $n$ un entier strictement positif. Supposons que $f_{n-1}$ est solution de $y'(x) + y(x) = f_{n-2}(x)$ . Alors la solution $f_n$ de $y'(x) + y(x) = f_{n-1}(x)$ telle que $f_n(0) = 0$ est donnée par la formule de la partie A :

$f_n(x) = \frac{x^n}{n!}e^{-x}$

En effet, la solution générale de $y'(x) + y(x) = f_{n-1}(x)$ est de la forme $y(x) = Ce^{-x} + f_{n-1}(x)$ pour une constante $C$ , et la condition $y(0) = 0$ donne $C = -f_{n-1}(0) = 0$ . On obtient ainsi que la solution $f_n$ de $y'(x) + y(x) = f_{n-1}(x)$ telle que $f_n(0) = 0$ est donnée par :

$f_n(x) = \frac{x^n}{n!}e^{-x}$

Ce résultat est vrai pour tout entier $n \geq 1$ , donc $\frac{x^n}{n!}e^{-x}$ est la solution de $(E_n)$ avec la condition initiale $f_n(0) = 0$ .

1b. Pour tout réel $x$ , on a $0 \leq xe^{-x} \leq e^{-x}$ , donc par récurrence sur $n$ et par la question 1a, on obtient :

$0 \leq |f_n(x)| = \frac{|x|^n}{n!}e^{-|x|} \leq \frac{|x|^n}{n!}$

En intégrant ces inégalités sur l’intervalle $[0,1]$ , on obtient :

$0 \leq I_n = \int_0^1 |f_n(x)| dx \leq \frac{1}{n!}\int_0^1 t^n dt = \frac{1}{(n+1)!}$

On en déduit que $0 \leq I_n \leq \frac{1}{(n+1)!}$ pour tout entier $n \geq 0$ . En utilisant le théorème des croissances comparées, on obtient que $\lim_{n \to +\infty} I_n = 0$ , donc la suite $(I_n)$ converge vers 0.

1c. Pour tout réel $x$ , on a $0 \leq |f_n(x)| \leq \frac{|x|^n}{n!}$ , donc en intégrant ces inégalités sur l’intervalle $[0,1]$ , on obtient :

$0 \leq I_n \leq \frac{1}{n!}\int_0^1 t^n dt = \frac{1}{(n+1)!}$

D’après la question précédente, la suite $(I_n)$ converge vers 0. En utilisant la question 2b, on a :

$I_n - I_{n-1} = -\frac{1}{n!}e^{-1}$

Donc la série $\sum_{k=0}^{+\infty} (I_k - I_{k-1})$ converge vers $-e^{-1}$ . D’après la question précédente, on a :

$I_n = 1 - \sum_{k=0}^{n-1} (I_k - I_{k-1}) = 1 + e^{-1} - \sum_{k=1}^{n-1} \frac{1}{k!}e^{-1} = 1 - \frac{1}{n!}e^{-1} + \frac{1}{n!}e^{-1}\sum_{k=0}^{n-1} \frac{1}{k!}$

Ainsi, » $(\sum_{k=0}^{n}\frac{1}{k!})$ converge vers » align= »absmiddle » />e^{-1} + \lim_{n \to +\infty} I_n = e^{-1} + 0 = e » align= »absmiddle » />.

1d. Par définition, $f_0(x) = e^{-x}$ , donc la solution de $(E_0)$ avec la condition initiale $f_0(0) = 0$ est $f_0(x) - f_0(0) = e^{-x}-1$ . D’après la question 2c de la partie A, la solution de $(E_n)$ avec la condition initiale $f_n(0) = 0$ est $\phi_n(x) = \frac{x^n}{n!}e^{-x}$ pour tout entier $n \geq 1$ .

Exercice 17 :

a. On a $\frac{1}{e^3}=e^{-3}$ .

b. On a $e^{-2}\times\,e^7=e^5$ .

Exercice 18 :

On a $g(x)=-2f(x)=-2e^{x}$ , donc $g'(x)=(-2e^{x})'=g(x)$ .

On a $g(0)=-2f(0)=-2 \times (-\frac{1}{2})=1$ , donc $g(x)=e^x$ .

En utilisant $f(x)=\frac{g(x)}{-2}=-\frac{1}{2}e^x$ , on trouve que $f'(x)=(-\frac{1}{2}e^x)'=-\frac{1}{2}e^x=f(x)$ .

Exercice 19 :

a. $e^4\times\,e^6=e^{10}$ .

b. $e\times(e^5)^2=e^{10}$ .

c. $\frac{e^{30}\times\,e^{-10}}{e^{10}}=e^{10}$ .

a. $\frac{e^{2a}\times\,e^{-a}}{e^{5a}}=e^{-2a}$ .

b. $\frac{e^{2a}+1}{e^{1-a}}=e^{3a}+e^a$ .

c. $(e^a)^3\times\,e=e^{4a}$ .

Exercice 20 :

1. On a $f'(x)=\frac{e^x(1-x)-e^x}{(1+x)^2}=\frac{e^x(x-2)}{(1+x)^2}$ , donc l’équation de $T_a$ est $y=f(a)+f'(a)(x-a)=\frac{e^a}{1+a}(x-a)+\frac{e^a}{1+a}$ , ou $y=\frac{e^a(x-a+1)}{1+a}$ .
2. On cherche les valeurs de a pour lesquelles la droite passe par l’origine,

c’est-à-dire pour lesquelles $T_a(0)=0$ ,

c’est-à-dire pour lesquelles a=1, puisque $T_a(0)=\frac{e^a(1-a)}{1+a}$ et que, pour $a>-1, 1-a>0$ et $1+a>0$ .

Donc il y a deux solutions : a=1 ou a=-2.

Exercice 21 :

a. Avant la mise en marche, t=0, donc $T(0)=19,5-10,5=9$ °C.

b. Après une journée de fonctionnement, $t=24\times\,60=1\,440$ , donc $T(1\,440)=19,5e^{-7\times\,10^{-4}\times\,1440}-10,5\approx -20,92$ °C.

2. On a $\lim_{t\to +\infty}T(t)=\lim_{t\to +\infty}(19,5e^{-7\times\,10^{-4}\times\,t}-10,5)= -10,5$ , donc la température moyenne tend vers -10,5°C quand le temps tend vers l’infini.

Exercice 22 :

a. $e^{-7}\times\,e^3=e^{-4}$ .

b. $e^{-1}\times\,e^{-5}=e^{-6}$ .

c. $e^2\times\,e=e^3$ .

d. $e\times\,e^{-1}=1$ .

e. $\frac{1}{e}=e^{-1}$ .

f. $\frac{1}{e^{-1}}=e$ .

g. $\frac{1}{e^2}=e^{-2}$ .

h. $\frac{1}{e^{-3}}=e^3$ .

i. $\frac{1}{e^{-3}}=e^3$ .

j. $\frac{e}{e^{-1}}=e^2$ .

k. $\frac{e^{-2}}{e}=e^{-3}$ .

l. $\frac{e^2\times\,e^{-3}}{e^5}=e^{-1}$ .

m. $(e^2)^3=e^6$ .

n. $(e^3)^2=e^6$ .

o. $(e^{-1})^6=e^{-6}$ .

p. $e\times\,(e^{-1})^3=e^{-2}$ .

Exercice 23 :

a. On a $e^x\times\,e^2=e^{x+2}$ .

b. On a $e^{-1}\times\,e^{-x}=e^{-x-1}$ .

c. $e\times\,e^x=e^{x+1}$ .

d. $e^x\times\,e^x=(e^x)^2$ .

e. $e^x\times\,e^{-x}=1$ .

f. $e^{x-1}\times\,e^x=e^{2x-1}$ .

g. $(e^x)^2=e^{2x}$ .

h. $(e^{-x+1})^3=e^{-3x+3}$ .

i. $(2e^x)^3=8\,e^{3x}$ .

j. $\frac{e^{5x}}{e^x}=e^{4x}$ .

k. $\frac{e^{x+1}}{e}=e^{x}$ .

l. $\frac{e^3}{e^{2x-1}}=e^{3+1-2x}$ .

Exercice 24 :

a. On a $f'(x)=0,5e^{0,5x}$ .

b. On a $f'(x)=e^{x+1}$ .

c. On a $f'(x)=2e^{2x}$ .

a. On a $f'(x)=0,5e^{0,5x}\leq 0$ pour $x\geq 0$ , donc f est décroissante sur $[0;+\infty[$ .

b. On a $f'(x)=e^{x+1}\leq 0$ pour $x\leq -1$ , donc f est décroissante sur $]-\infty;-1]$ .

c. On a $f'(x)=2e^{2x}>0$ pour tout x, donc f est croissante sur $\mathbb{R}$ .

Exercice 25 :

1. On a $\lim_{x\to +\infty}f(x)=\lim_{x\to +\infty}(17280e^{-0,024x})=0$ , donc la limite de f en $+\infty$ est 0.

2. On a $f'(x)=(-0,024\times 17280e^{-0,024x})=-414,72e^{-0,024x}$ , qui est strictement négative sur $[15;+\infty[$ , donc f est décroissante sur cet intervalle.

3. La conjecture est que la fonction f est décroissante sur $\mathbb{R}$ , ce qui est effectivement vrai d’après 2.

En effet, la dérivée est strictement négative sur tout l’intervalle de définition de f, donc f est décroissante sur cet intervalle.

Exercice 26 :

1. On a $f'(x)=-e^x+1$ .

2. On a $f'(x)=-e^x+1\leq 0$ pour tout $x\in[0;+\infty[$ , donc f est décroissante sur cet intervalle.

3. On sait que f est décroissante sur $[0;+\infty[$ , donc son maximum est atteint en x=0 et son minimum en $x=+\infty$ .

On peut calculer f(0)=2 et $\lim_{x\to+\infty}f(x)=-\infty$ .

On a également $\lim_{x\to-\infty}f(x)=+\infty$ (car $e^x$ tends vers 0 plus vite que x tend vers -∞) et f est décroissante sur $]-\infty;0]$ .

Donc le tableau de variation de f est :

x | $]-\infty;0]$ | 0 | $[0;+\infty[$
f'(x) | + | 0 | –
f(x) | $+\infty$ | 2 | $-\infty$

Exercice 27 :

a. On a $\frac{e^{2x+1}}{e^{1-x}}=e^{3x+1}$ .

b. On a $\frac{e^{-x+2}\times\,e^{-2x-1}}{e^{3x+2}\times\,e^{-x-1}}=\frac{1}{e^{6x+3}}=e^{-6x-3}$ .

c. On a $\frac{(e^{-x})^2\times\,e^{-x+1}}{e^{x+2}\times\,(e^{-x-1})^3}=\frac{e^{-2x+1}}{(e^{-2x-3})^3}=\frac{1}{e^{4x+10}}=e^{-4x-10}$ .

Exercice 28 :

On a $-2e^{2x}+3e^x+2=-2(e^x)^2+3e^x+2=(1-2e^x)(2-e^x)$ .

On a $\frac{e\times\,e^x}{e^{2+3x}}=\frac{e^{x+1}}{e^{3x+2}}=\frac{e^{-(-x-1)}}{e^{-3x-2}}=(e^{-x-0,5})^2$ .

On a $\frac{e^{1-3x}}{1+e^{-3x}}=\frac{e^{3x+1}}{e^{3x}+1}=\frac{e^{3x}e^{-3x-1}}{e^{3x}(e^{-3x}+1)}=\frac{e}{e^{-3x}+1}$ .

Exercice 29 :

1) En posant $y=e^x$ , on peut réécrire l’équation $e^x-2e^{-x}+1=0$ sous la forme $y^2+y-2=0$ .

Cette dernière équation correspond à une équation du second degré se factorisant en $(y-1)(y+2)=0$ .

Donc, on a $y-1=0$ ou $y+2=0$ , c’est-à-dire $e^x-1=0$ ou $e^x=-2$ .

Or, $e^x$ est toujours strictement positif, donc on ne peut pas avoir $e^x=-2$ .

Ainsi, l’équation $e^x-2e^{-x}+1=0$ est équivalente à l’équation $(e^x)^2+e^x-2=0$ .

2) On vient de montrer que $(e^x)^2+e^x-2=0$ est équivalente à $e^x-2e^{-x}+1=0$ .

On peut donc résoudre l’équation $(e^x)^2+e^x-2=0$ .

En posant $y=e^x$ , on a $y^2+y-2=0$ , qui correspond à une équation du second degré se factorisant en $(y-1)(y+2)=0$ .

Ainsi, on a $y-1=0$ ou y+2=0, c’est-à-dire $e^x=1$ ou $e^x=-2$ .

Or, e^x ne peut pas être négatif, donc on ne peut pas avoir $e^x=-2$ .

D’où la solution de l’équation $e^x-2e^{-x}+1=0$ est $x=\ln 1=0$ .

Exercice 30 :

1) On peut réécrire l’inéquation $e^{-x}-e^x>0$ sous la forme $\frac{1}{e^x}-e^x>0$ , c’est-à-dire $\frac{1-e^{2x}}{e^x}>0$ . Ainsi, on a deux cas à étudier :
– Si $e^x>0$ , alors l’inéquation équivaut à $1-e^{2x}>0$ , c’est-à-dire $e^{2x}<1$ , d’où x<0.
– Si $e^x<0$ , alors l’inéquation équivaut à $1-e^{2x}<0$ , c’est-à-dire $e^{2x}>1$ , d’où $x>\ln 1=0$ .
Finalement, la solution de l’inéquation $e^{-x}-e^x>0$ est x<0.

2) On peut réécrire $1-\frac{1+e^x}{1+e^{-x}}$ sous la forme $\frac{e^{-x}-e^x}{1+e^{-x}}$ .

On vient de montrer que $e^{-x}-e^x>0$ pour tout $x<0$ , donc le numérateur est négatif dans cette intervalle.

De plus, le dénominateur est toujours positif.

Ainsi, $1-\frac{1+e^x}{1+e^{-x}}$ est négatif sur $\mathbb{R}_-^*$ .

Exercice 31 :

Conjecture : On a $\lim_{x \to 0}\frac{e^x+1}{x}=2$ et $\lim\limits_{x \to \pm \infty}\frac{x+1}{e^x}=0$ .

Démonstration :

– Pour la limite en 0, on peut utiliser le développement limité de $e^x$ au premier ordre au voisinage de 0 : $e^x=1+x+o \times x$ .

Ainsi, on a $\frac{e^x+1}{x}=2+o \times 1$ , d’où $\lim_{x \to 0}\frac{e^x+1}{x}=2$ .
– Pour la limite en $+\infty$ , on a $\frac{x+1}{e^x}\leq \frac{x}{e^x}$ , qui tend vers 0 quand x tend vers $+\infty$ .
– Pour la limite en $-\infty$ , on peut réécrire $\frac{x+1}{e^x}$ sous la forme $\frac{1+\frac{1}{x}}{e^{-x}}$ , qui tend vers 0 quand x tend vers $-\infty$ .

En effet, on a $\lim_{x \to -\infty}\frac{1}{x}=0$ et $\lim\limits_{x \to -\infty}e^{-x}=+\infty$ .

4.5/5 - (22005 votes)

Fonction exponentielle : corrigé des exercices en terminale en PDF.

Fonction exponentielle : corrigé des exercices de maths en terminale en PDF.

Limites de fonctions : corrigé des exercices de maths en 1ère en PDF.

Géométrie dans l'espace : corrigé des exercices en 1ère en PDF.

Trigonométrie : corrigé des exercices de maths en 1ère en PDF.