Arithmétique et nombres premiers : cours de maths en 3ème.

Arithmétique et les nombres premiers dans un cours de maths en 3ème au cycle 4. Nous aborderons les notions de multiple et diviseur, les critères de divisibilités. Nous étudierons, également, les nombres premiers et le crible d’Erastostène puis la décomposition en facteurs premiers d’un nombre entier positif ainsi que les fractions irréductibles dans cette leçon en troisième.

I. La division euclidienne

1.Division euclidienne

Propriété :

On considère $a$ et b deux nombres entiers positifs avec b non nul.

Effectuer la division euclidienne de $a$ par $b$ , c’est trouver le couple unique d’entiers positifs q et r

vérifiant :

$a=b\times q+r$ avec $r<b$ .

Exemple :

Prenons a=187 et b=13.

On pose la division euclidienne pour obtenir q et r.

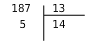
donc $187=13\times 14+5$ avec 5<13.

2. Multiples et diviseurs

Définition :

On considère a et b deux entiers positifs avec b non nul.
Si r=0 alors l’égalité précédente devient $a=b\times q$ .
On dit alors que $a$ est un multiple de $b$ et que $b$ est un diviseur de $a$
ou encore que $b$ divise $a$ .

Exemple:

Prenons a=135 et b=15.

On a $135=15\times 9+0=15\times 9$ .

Donc 135 est un multiple de 15 et 15 est un diviseur de 135.

De même 135 est un multiple de 9 et 9 est un diviseur de 135.

Remarques :

Un nombre entier a un nombre fini de diviseurs mais un nombre infini de multiples;
Un nombre entier supérieur à 1 admet toujours au moins deux diviseurs qui sont 1 et lui-même.

3. Critères de divisibilité

Propriété :

Un nombre entier est divisible par 2 si le chiffre de ses unités est 0,2,4,6 ou 8.Dans ce cas, on dit qu’il est pair;
Un nombre entier est divisible par 3 si la somme de ses chiffres est un multiple de 3;
Un nombre entier est divisible par 4 si le nombre constitué de ses deux derniers chiffres (dizaine et unité) est divisible par 4;
Un nombre entier est divisible par 5 si le chiffre de ses unités est 0 ou 5;
Un nombre entier est divisible par 9 si la somme de ses chiffres est un multiple de 9.

Exemple :

915 n’est pas divisible par 2 car il ne se termine pas par 0,2,4,6 ou 8.
915 est divisible par 3 car 9+1+5=15 et 15 est un multiple de 3. 915 n’est pas divisible par 4 car 15 n’est pas divisible par 4.D’ailleurs comme il n’est pas divisible par 2, il ne peut pas être divisible par 4.
915 est divisible par 5 car il se termine par 5.
915 n’est pas divisible par 9 car 9+1+5=15 et 15 n’est pas un multiple de 9.

II. Les nombres premiers

1.Définition

Définition :

Un nombre est dit premier, s’il admet exactement 2 diviseurs distincts (lui-même et l’unité). 1 n’est donc pas premier.

2. Le crible d’Eratosthène

n désigne sous le nom de crible d’Eratosthène (vers 276 av.J.-C – vers 194 av.J.-C), une méthode de recherche des nombres premiers plus petits qu’un entier naturel n donné.
Pour ceci, on écrit la liste de tous les nombres jusqu’à n.

On élimine 1.
Puis on fait de même avec 3.
On choisit alors le plus petit nombre non souligné et non éliminé ici 5, et on élimine tous ses multiples.
On réitère le procédé jusqu’à la partie entière de la racine de n.

Les nombres non éliminés sont les nombres premiers jusqu’à n.

Exemple :

Les nombres premiers inférieurs à 100 sont donc 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

3. Décomposition en facteurs premiers

Propriété :

Tout nombre entier $n$ supérieur à 1 peut s’écrire sous la forme d’un produit de nombres premiers.Quand on écrit la décomposition sous la forme $n=p_1^{a1}\times p_2^{a_2}\times ...\times p_k^{a_k}$

avec $p_1<p_2<...<p_k$ des nombres premiers.

Cette écriture est unique et est appelée décomposition en facteurs premiers de l’entier $n$ .

Exemple :

On veut décomposer l’entier 3 626 en produit de facteurs premiers.

2 est un diviseur de 3 626 donc 3 626 = 2×1 813.On essaie maintenant de décomposer 1 813.

7 est un diviseur de 1 813 donc 3 626=2x7x259.On essaie maintenant de décomposer 259.

7 est un diviseur de 259 donc 3 626=2x7x7x37.On essaie maintenant de décomposer 37.

37 est un nombre premier donc la décomposition en facteurs premiers de 3 626 est $3626=2\times 7^2\times 37$ .

4. Fractions irréductibles

Définition :

Une fraction est dite irréductible quand ce n’est plus possible de la simplifier donc lorsque le seul diviseur en commun du numérateur et du dénominateur est 1.

Exemple :

$\frac{14}{21}$ n’est pas une fraction irréductible car $\frac{14}{21}=\frac{14:7}{21:7}=\frac{2}{3}$ .Par contre $\frac{2}{3}$ est une fraction irréductible.

Remarque :

Pour écrire une fraction sous la forme irréductible, on décompose son numérateur et son dénominateur en produit de facteurs premiers, et on simplifie.

Quand on ne peut plus simplifier, la fraction est irréductible.

Exemple :

$\frac{168}{3626}=\frac{2^3\times 3\times 7 }{2\times 7^2\times 37}=\frac{2\times 2\times 2\times 3\times 7}{2\times 7\times 7\times 37}=\frac{2\times 2\times 3}{7\times 37}=\frac{12}{259}$