Fonctions linéaires : cours de maths en 3ème en PDF.
Sommaire
ToggleDans cette leçon on considérera un repère
I.Les fonctions linéaires :
1. Activité d‘introduction :
Un tissu coûte 3 euros le mètre chez un grossiste.
Un client effectue une commande, nous allons étudier le prix de sa commande vis-à-vis de la longueur de tissus achetée.
a. Compléter le tableau suivant :
| Longueur (en m) | 1 | 2 | 3 | 4 |
| Prix ( en € ) | 3 | 6 | 9 | 12 |
b. Ce tableau est-il un tableau de proportionnalité ?
Oui car :
.
Tous les rapports sont égaux, donc c‘est un tableau de proportionnalité.
Le prix et la longueur du tissus sont donc proportionnels.
Le coefficient de proportionnalité est 3.
c. Notons x : la longueur du tissus en mètre,
et y : le prix du tissus en euros.
Donner une relation (égalité) entre x et y.
Nous avons y = 3x.
Remarque :
y est une « fonction linéaire » de x.
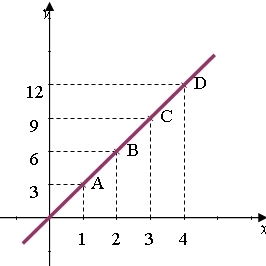
d. Placer les points A (1 ;3) B(2 ;6) C(3 ;9) D(4 ;12) dans le repère 
e. Quelles sont vos remarques ?
Tous les points sont alignés sur une même droite et cette droite passe par l‘origine O du repère.
2. les fonctions linéaires
Soit a un nombre relatif connu et fixé.
La fonction linéaire de coefficient a est un objet mathématique définie par la relation suivante :
A un nombre x, on fait correspondre le produit ax
(c’est-à-dire se lit « la fonction f qui à x associe ax »)
ou encore la fonction f définie par f(x)=ax.
Le nombre f(x) est appelé l‘image de x par la fonction f.
Exemples :
Dans l‘activité précédente, le prix est une fonction linéaire de la longueur du tissu.
C‘est une fonction linéaire de coefficient a=3
Elle se note : .
On note : où 6 est l‘image de 2 par la fonction f ou f(2)=6.
On lit « f de 2 est égal à 6 ».
Soient les fonctions f,g, h telles que et
.
– Quelle(s) sont le(s) fonction(s) linéaire(s) ?
La seule est f car elle est du type f(x)=ax avec a=2.
– Calculer l‘image de 4 par les fonctions f, g et h.
3. Représentation graphique d‘une fonction linéaire :
D’après l‘activité précédente, nous avons observé que tous les points étaient alignés sur une droite passant par l‘origine.
Cette propriété est généralisée à toutes les fonctions linéaires.
La représentation graphique d‘une fonction linéaire de coefficient a est une droite passant par l‘origine du repère.
Le nombre a est appelé « coefficient directeur » de la droite.
Remarque:
Toute situation de proportionnalité débouche sur une fonction linéaire.
Le nombre a s‘appelle le coefficient directeur, il indique la direction de la droite représentative.
Il donne l‘accroissement de f(x) lorsque x augmente de 1.
(c‘est le coefficient de proportionnalité entre les accroissements de f(x) et de x).
Exemples :
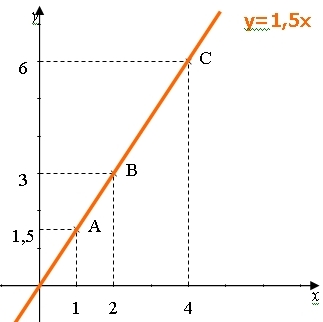
– La droite d représente la fonction linéaire : .
– Le coefficient directeur de la droite d est 1,5.
C‘est l‘ordonnée du point de la droite d d‘abscisse 1.
– Les coordonnées (x ;y) d‘un point de la droite d vérifie l‘équation : y=1,5x.
– On dit que la droite d a pour équation réduite : y=1,5x.
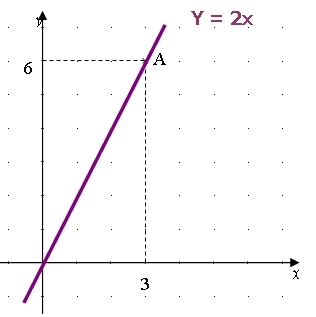
– Représenter graphiquement la fonction f définie par
C‘est une fonction linéaire donc sa courbe représentative est une droite qui passe par l‘origine
donc pour la tracer il nous suffit donc de trouver les coordonnées d‘un autre point appartenant à cette droite.
On prend une valeur quelconque de x et on calcule son image f(x).
| Valeur de x | 3 |
| Valeur de f(x) | 6 |
| Point de la droite | A(3 ;6) |
On trace la droite passant par les points O et A.
II.Détermination de l‘expression algébrique d‘une fonction linéaire :
La donnée des coordonnées d‘un point A distinct de l‘origine O est suffisante pour pouvoir déterminer l‘expression algébrique d‘une fonction linéaire.
Exemple :
Cherchons l‘expression de la fonction linéaire f telle que le point A (3 ;12) appartienne à la droite représentative de f.
Nous savons que l‘équation de la droite est du type y=ax
L‘objectif est de déterminer la valeur de a.
On remplace les coordonnées dans l‘égalité et on résout l’équation.
y=ax
12 = ax3
soit 12 :3=a
d‘où a=4
Conclusion :
la fonction f est définie par f(x)=4x ou .
Trouver l‘expression de la fonction :
g telle que B(2 ; 0,8) appartienne à sa courbe.
h telle que B(5 ;-10) appartienne à sa courbe.
Réponse :
et
.
Vous avec assimilé ce cours sur les fonctions linéaires en 3ème ?
Effectuez ce QCM sur les fonctions linéaires afin d’évaluer vos acquis sur cette leçon en troisième.
Résumé-Quiz
0 questions correctes sur 13
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
Information
Un QCM sur les fonctions linéaires.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 13 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Répondu
- Examiner
-
Question 1 sur 13
Si f est une fonction telle que f(2)=5, alors
Exact
Inexact
-
Question 2 sur 13
Parmi les fonctions suivantes, la fonction linéaire est
Exact
Inexact
-
Question 3 sur 13
L’image de – 3 par
est
Exact
Inexact
-
Question 4 sur 13
La fonction linéaire h telle que h(5) = – 3 est
Exact
Inexact
-
Question 5 sur 13
L’antécédent de – 9 par la fonction linéaire
est
Exact
Inexact
-
Question 6 sur 13
On considère le tableau de proportionnalité suivant :
x 9 0 12
f(x) 6 0 8
La fonction linéaire associée est
Exact
Inexact
-
Question 7 sur 13
Pour obtenir une valeur diminuée de 5 %, on peut
Exact
Inexact
-
Question 8 sur 13
La fonction linéaire définie par f(x) = 1,15x traduit
Exact
Inexact
-
Question 9 sur 13
Nous avons f (5) = 3
Exact
Inexact
-
Question 10 sur 13
Soit f la fonction linéaire définie par f(x)= – 3x.
Exact
Inexact
-
Question 11 sur 13
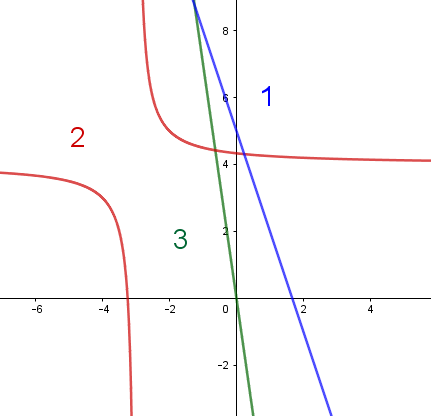
Voici les courbes représentatives de trois fonctions.
Parmi ces différentes courbes, quelle est celle qui
représente une fonction linéaire ?
Exact
Inexact
-
Question 12 sur 13
Soit la courbe d’une certaine fonction linéaire ci-dessous :
L’antécédent de 2 par cette fonction est :
Exact
Inexact
-
Question 13 sur 13Exact
Inexact