
Généralités sur les fonctions numériques : cours de maths en 2de en PDF.
Sommaire
ToggleI. Opérations algébriques sur les fonctions :
1. Egalité :
Dire que deux fonctions f et g sont égales, ce que l’on note alors f = g, signifie qu’elles ont le même ensemble de définition D et que, pour tout x de D, f(x) = g(x).
2. Opérations :
Soient f et g deux fonctions définies respectivement sur Df et Dg.
Opérations :
| Opération | Notation | Definition | Definie pour : |
| Somme | f+g | ||
| Différence | f-g | x |
|
| Produit | fg | x |
|
| quotient | x |
3. Composition de fonctions :
Etant donné deux fonction f et g, la fonction gof (lire « g rond f ») est la fonction definie par
L’ensemble de définition de gof est constitué de tous les nombres x tels que x soit dans Df et f(x) soit dans Dg.
Exemple :
f est la fonction définie sur R par f(x)=x-2 et g est la fonction carrée.
Dans g(x), on remplace x par f(x).
Alors g(f(x))= (x-2)²
Donc gof est la fonction x 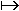
II. Sens de variation:
1. Sens de variation d’une somme de fonction :
- La somme de deux fonctions strictement croissantes sur un intervalle I est une fonction strictement croissante sur I.
- La somme de deux fonctions strictement décroissantes sur un intervalle I est une fonction strictement décroissante sur I.
2. Sens de variation de ku :
Soit u une fonction définie sur un intervalle I et k un nombre réel.
ku est la fonction x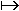
Exemple :
si u(x)=x²+3, la fonction 5u (ici k=5) est x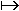
- Si k>0, u et ku ont le même sens de variation sur I.
- Si k<0, u et ku varient en sens contraires sur I.
3. Sens de variation d’une composée de fonctions :
Soient f et g deux fonctions strictement monotones, I est un intervalle inclus dans Df,
J un intervalle inclus dans Dg tel que pour tout x dans I, f(x) soit dans J.
- Lorsque f et g ont même sens de variation, alors gof est strictement croissante sur I.
- Lorsque f et g ont des sens de variation différents, alors gof est strictement décroissante sur I.
Vous avez assimilé ce cours sur les généralités sur les fonctions en 2de?
Effectuez ce QCM sur les fonctions numériques en classe de seconde.
Résumé-Quiz
0 questions correctes sur 10
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Un QCM sur les généralités sur les fonctions numériques en seconde.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 10 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Répondu
- Examiner
-
Question 1 sur 10
On considère la fonction f définie par
Quelle est l’image de 1 par f ?
- (-15)
Exact
Inexact
-
Question 2 sur 10
Quelles est la définition de la fonction suivante :
?
Exact
Inexact
-
Question 3 sur 10
Choisissez les propriétés qui sont vraies :
Exact
Inexact
-
Question 4 sur 10
Soit les fonctions numériques f et g définies ci-dessous.
Développer, réduire et ordonner ces expressions littérales.
Quel résultat obtenez-vous ?
f(x) = 9x + (5x – 2)²
g(x) = -5x – (3x +2)².Exact
Inexact
-
Question 5 sur 10
Quelle est la forme factorisée de l’expression suivante :
f(x) = 4x² – 16 – (4 + 2x)(5x – 6) ?
Exact
Inexact
-
Question 6 sur 10
Soit x et y des réels positifs non nuls représentant chacun la longueur y et la largeur x (en cm) d’un rectangle dont l’aire est égale à 30cm² et le périmètre a pour longueur 22cm. Quelle ensemble de fonction permettent de définir y en fonction de x ?
Exact
Inexact
-
Question 7 sur 10
Soit la fonction f définie par f(x) = -5x² + 10x + 3.
Quelle est l’image de
?
Exact
Inexact
-
Question 8 sur 10
Quelle est l’équivalent de
?
Exact
Inexact
-
Question 9 sur 10
Soit une fonction f définie tel que
, sur l’intervalle
.
Pourquoi la fonction f n’est-elle pas définie pour?
Exact
Inexact
-
Question 10 sur 10
Soit une fonction f définie tel que
, sur l’intervalle
.
Quel est l’image de?
- (-3)
Exact
Inexact

