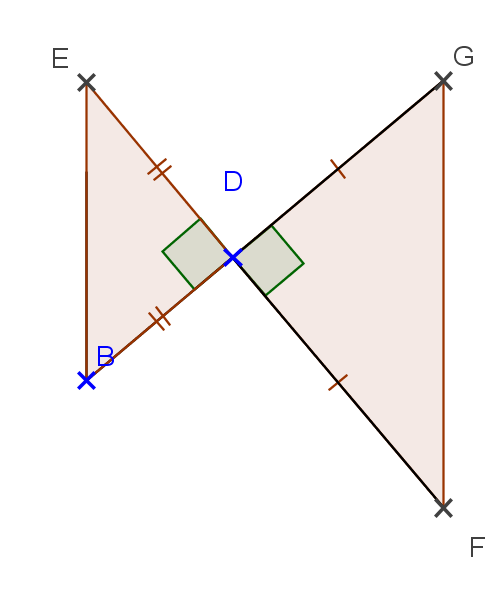
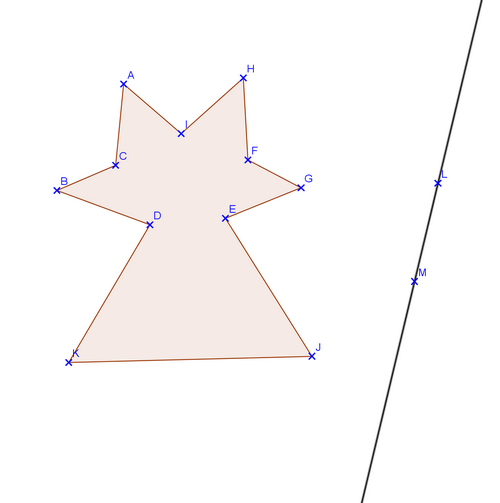
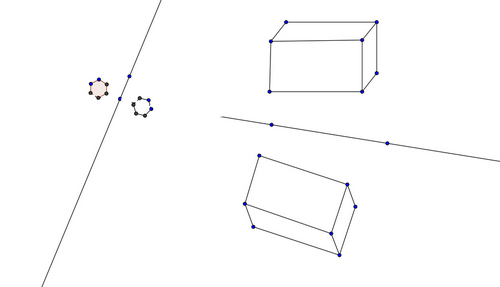
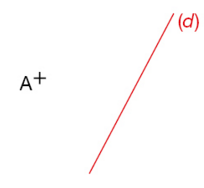
Exercice 1 – Axe de symétrie d’une figure

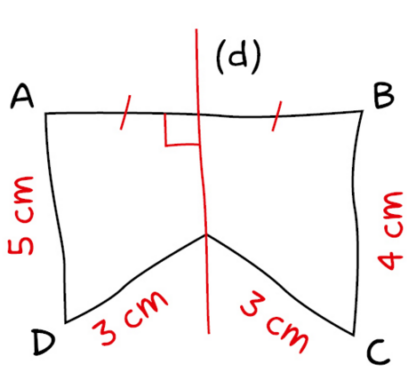
a. Faire cette figure sur papier blanc avec :

A,B,E alignés;

A,C,D alignés;

AB= 2 cm et AD= 4 cm.

b. Cette figure admet-elle un axe de symétrie ?

Si oui, tracer-le.

Exercice 2 – Symétrie axiale et triangles

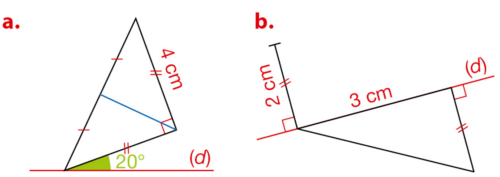
1.a. Construire un triangle ABC rectangle en A tel que :

AB= 4 cm et AC = 2 cm.

b. Ce triangle admet-il un axe de symétrie ?Si oui, tracer-le.

2.a. Construire un triangle MNP rectangle et isocèle en N tel que Nm = 5 cm.

b. Ce triangle admet-il un axe de symétrie ?

Si oui, tracer-le.

Exercice 3 – Figure et symétrie axiale

Construire la figure symétrique par rapport à la droite (LM).

Exercice 4 – Symétrie axiale d’une figure

Construire la symétrie axiale de cette figure par rapport à la droite (LM).

Exercice 5 – Constructions par symétrie axiale.

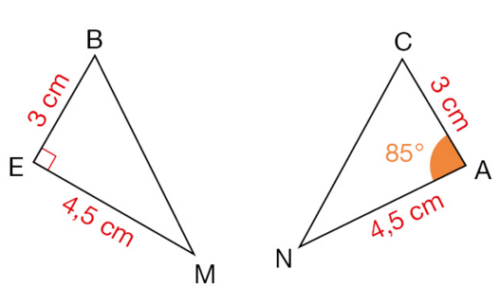
Exercice 6 – La symétrie axiale.

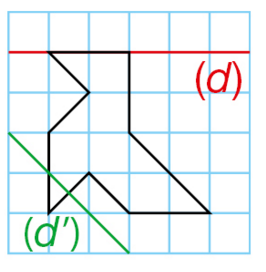
Exercice 7 – Symétrie axiale et quadrillage.

Dans chaque cas, construire l’image de la figure par la symétrie axiale d’axe (d).

Exercice 8 :

Construire avec la règle, l’équerre et le compas le symétrique A’ du point A
par rapport à la droite (d).

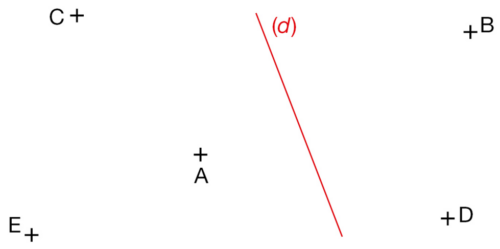
Exercice 9 :

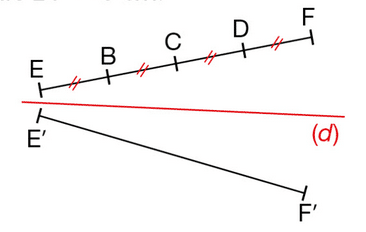
Tracer cette figure et construire les symétriques des points A, B, C, D, E par rapport à la droite (d).

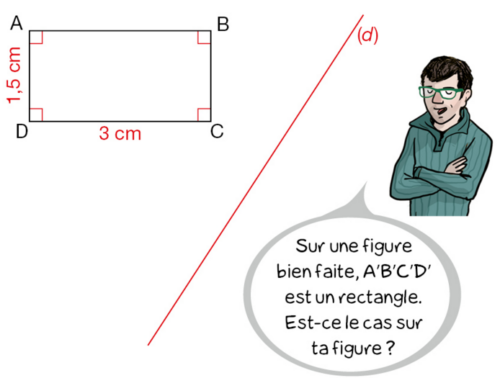
Exercice 10 :

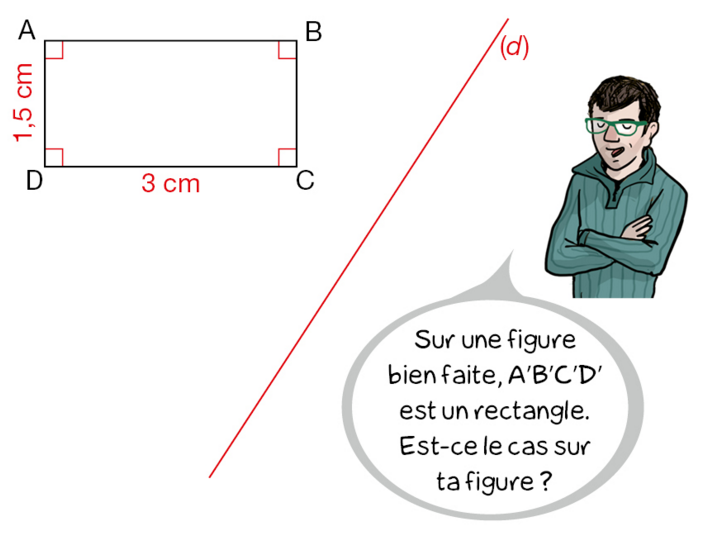
Tracer cette figure. Avec les instruments de géométrie, construire le symétrique du rectangle
ABCD par rapport à la droite (d).

Exercice 11 :

Sur la figure ci-dessous, on a commencé à construire le symétrique du quadrilatère ABCD par
rapport à la droite (d).
Sur une photocopie de cette figure, construire avec la règle graduée et le rapporteur :
• le symétrique D’ du point D par rapport à la droite (d),
• le symétrique C’ du point C par rapport à la droite (d).

Exercice 12 :

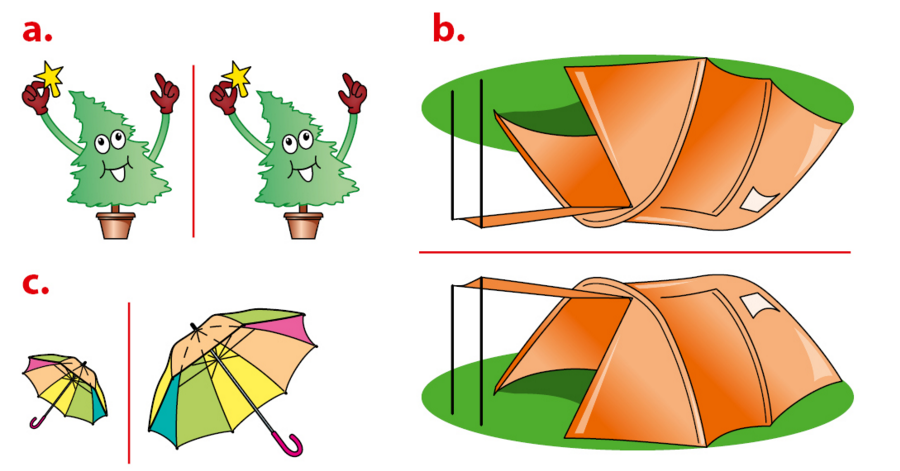
Dans chaque cas, dire si les deux dessins semblent symétriques par rapport à la droite rouge.
Sinon, dire pourquoi.

Exercice 13 :

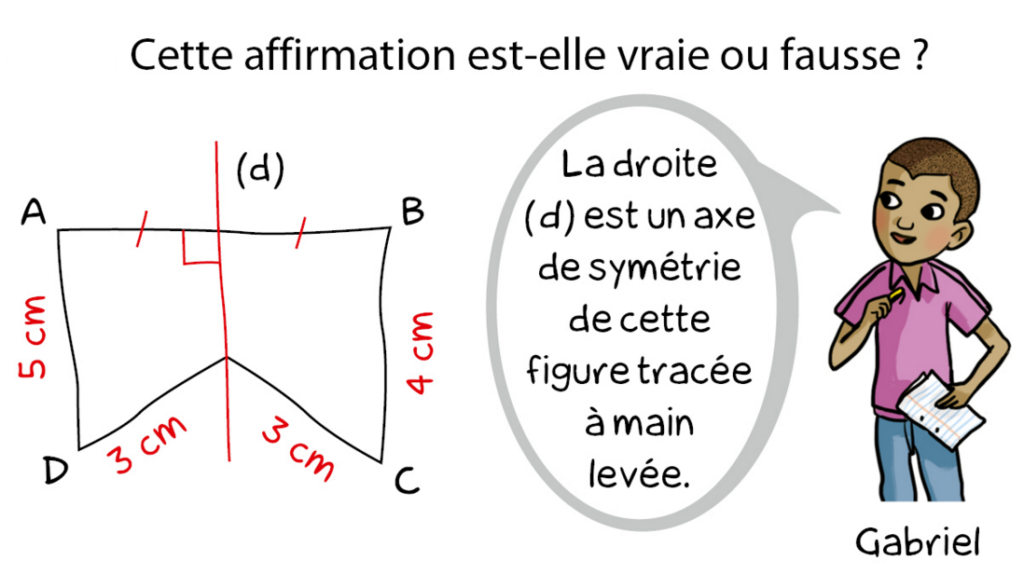
Cette affirmation est-elle vraie ou fausse ? Justifier.

Exercice 14 :

1.Tracer cette figure sur papier quadrillé.
2.Tracer la symétrique de la « cocotte » par rapport :
a. à la droite (d) ;
b. à la droite (d’).

Exercice 15 :

On suppose que chaque carreau de ce quadrillage a pour côté 1 cm.
a. Calculer le périmètre et l’aire de la figure  ci-dessous.

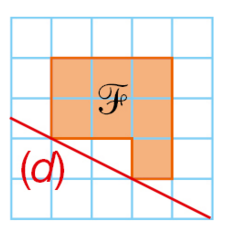
b. est la symétrique de par rapport à la droite (d).
Peut-on prévoir le périmètre et l’aire de la figure ?
Si oui, quels sont-ils ?

Exercice 16 :

On considère la figure suivante :

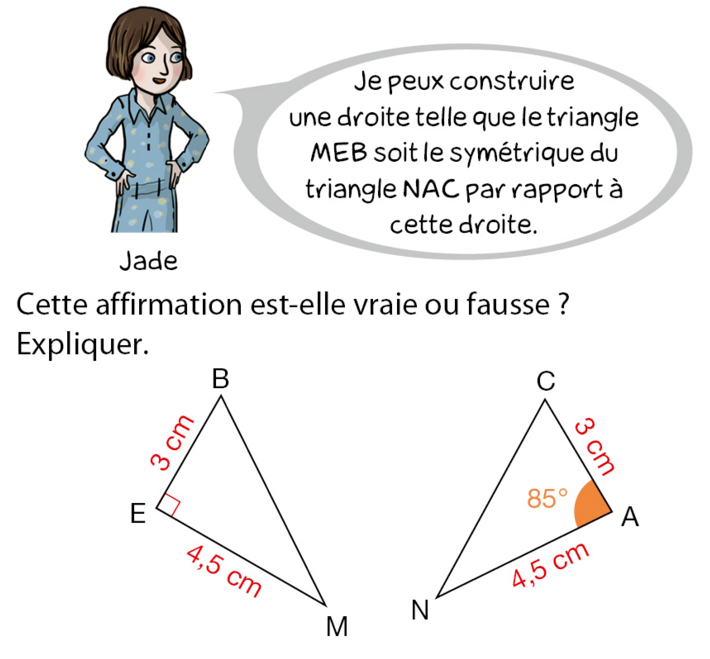
Cette affirmation est-elle vraie ou fausse ?

Exercice 17 :

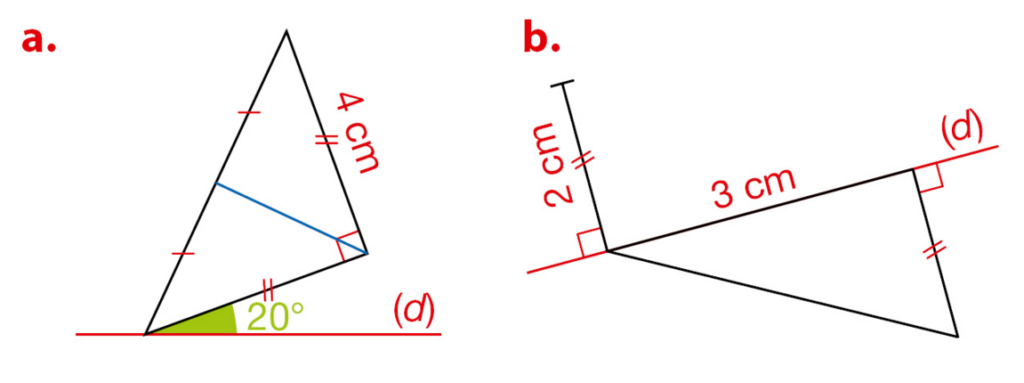
Construire chaque figure sur papier uni et la compléter pour que la droite (d) soit axe de symétrie.

Exercice 18 :
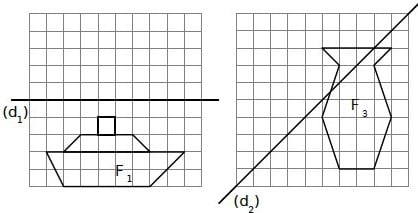
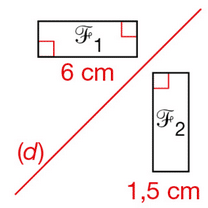
En te servant du quadrillage :
a. Trace la figure F2 symétrique de la figure F1 par rapport à la droite (d1).
b. Trace la figure F4 symétrique de la figure F3 par rapport à la droite (d2).

Exercice 19 :

Pour chaque couple de figures ci-dessous, dis sans justifier si les deux figures sont symétriques.

Exercice 20 :

a. En laissant les traits de construction, trace au compas le symétrique F6 de la figure F5 par rapport à la droite (d3).
b. En laissant les traits de construction, trace à l’équerre le symétrique F8 de F7 par rapport à la droite (d4).

Exercice 21 :
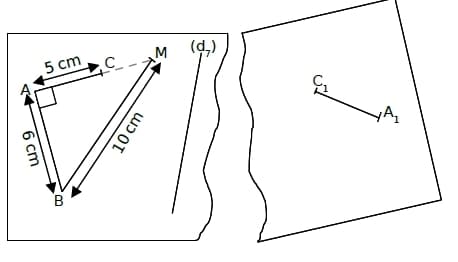
Samira a commencé à tracer le symétrique de la figure de gauche par rapport à la droite (d7) mais sa feuille s’est déchirée.

Elle a déjà placé le point C1, symétrique de C par rapport à (d7) et le point A1,symétrique de A. On ne demande pas de finir la figure mais d’expliquer comment, sans recoller la feuille, Samira peut finir sa construction. A chaque fois, tu devras citer toutes les propriétés du cours qui rendent la construction possible.
a. Explique, en citant deux propriétés, comment Samira va placer B1, le symétrique du point B par rapport à (d7).
b. Samira n’a pas de rapporteur et a décidé de ne pas mesurer la distance entre A et M.

Explique, en citant deux propriétés, comment elle va tout de même pouvoir placer M1, le symétrique du point M par rapport à (d7).
Le professeur vient de dire à Samira que l’aire du triangle AMB de l’exercice 4 est 24 cm².

Quelle est l’aire du triangle symétrique A1B1M1 ? Justifie en citant une propriété du cours.

Exercice 22 :

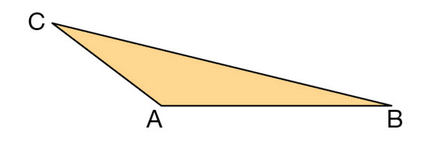
a. Tracer un triangle ABC comme ci-dessous.

b. Construire les points :

•  A’ symétrique de A par rapport à la droite (BC) ;
•  B’ symétrique de B par rapport à la droite (AC) ;
•  C’ symétrique de C par rapport à la droite (AB).

Exercice 23 :

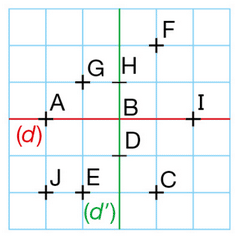
1. Quel est le symétrique par rapport à la droite (d) de :

a. C ?    b. A ?

c. H ? d. B ?

2. Quel est le symétrique par rapport à la droite (d’) de :
a. C ?     b. A ?

c. H ? d. B ?

3. Indiquer une droite, non tracée sur la figure, par rapport à laquelle les points A et B sont symétriques.

Exercice 24 :

Les figures et sont symétriques par rapport à la droite (d).
Calculer mentalement le périmètre et l’aire de la figure .

Exercice 25 :

Le segment [ET’] est le symétrique du segment [EF] par rapport à la droite (d).

Dans chaque cas, calculer mentalement la longueur demandée.

a. E’F’ lorsque BC = 1,3 cm.
b. EC lorsque E’F’ = 13,5 cm.
c. ED lorsque E’F’ = 8 cm.

Exercice 26 :

Tracer cette figure.
Construire le symétrique A’ du point A et le symétrique B’ du point B par rapport à la droite (d).

Exercice 27 :

Tracer cette figure.
Construire le symétrique M’ du point M par rapport à la droite (d).

Exercice 28 :

Tracer cette figure.

Avec les instruments de géométrie, construire le symétrique du rectangle
ABCD par rapport à la droite (d).

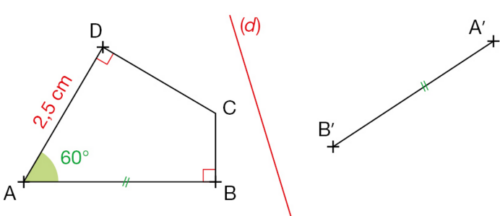
Exercice 29 :

Sur la figure ci-dessous, on a commencé à construire le symétrique du quadrilatère ABCD par
rapport la droite (d).

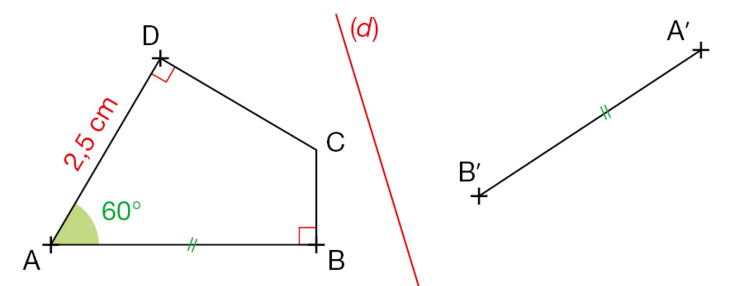
Sur une photocopie de cette figure, construire avec la règle graduée et le rapporteur :
• le symétrique D’ du point D par rapport à la droite (d),
• le symétrique C’ du point C par rapport à la droite (d).

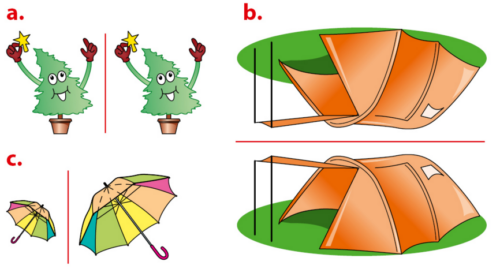
Exercice 30 :

Dans chaque cas, dire si les deux dessins semblent symétriques par rapport à la droite rouge.
Sinon, dire pourquoi.

Exercice 31 :

Exercice 32 :

Exercice 33 :

Construire chaque figure sur papier et la compléter pour que la droite (d) soit axe de symétrie.