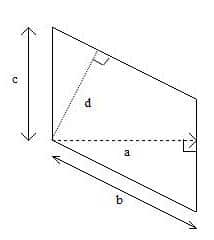
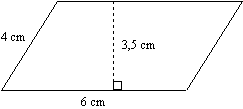Exercice 1 :
Exercice 2 :
Exercice 3 :
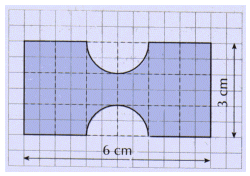
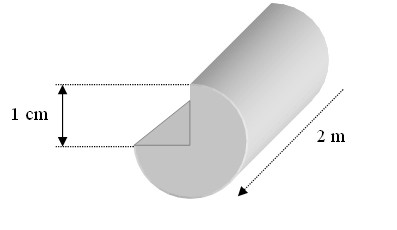
Calculer l’aire du rectangle.
Calculer l’aire du demi-disque.
Calculer l’aire totale.
Exercice 4 :
Exercice 5 :
Exercice 6 :
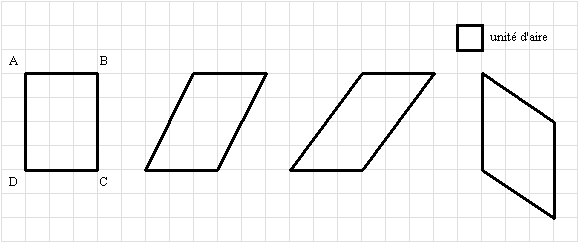
Premier parallélogramme, un rectangle, dont l’aire se calcule par le produit de deux côtés consécutifs.
Aire (ABCD) = 3*4 = 12 unités d’aire
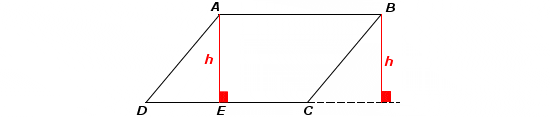
Pour calculer les aires des autres parallélogrammes utilisons ce schéma :
De manière générale hxAB nous donne l’Aire.
Deuxième parallélogramme, il nous faut déterminer h
On voit que de haut en bas, h vaut 4 et la base vaut 3. Donc l’aire est de 12 unités d’aire.
Troisième parallélogramme, il nous faut déterminer h
De haut en bas, h vaut toujours 4 unités d’aire tandis que la base vaut 3 unités d’aires
L’aire est donc de 12 unités d’aire.
Quatrième et dernier parallélogramme, il nous faut déterminer h
De gauche à droite, h vaut 3 unités d’aire, et sa base (un des côté verticaux) vaut 3 unités d’aires. L’aire est encore de 12 unités d’aire!
Exercice 7 :
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|||||||
|
|
ha |
a |
ca |
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 m² = 100 dm² = 10 000cm² = 1 000 000 mm²
1 m² = 0,01 dam² = 0,000 1 hm² = 0,000 001 km²
ca = 1 m² 1 a = 1 dam² 1 ha = 1 hm²
1. Complèter :
360 cm² = 3,6 dm² 1 km² = 1 000 000 m² 10 000 m² = 1 hm²
8 m² = 800 dm ² = 80 000 cm² .
145 cm² = 0,0145 m² = 14 500 mm²
0,1 dam ² = 10 m² = 0,000 01 km²
2. Complèter :
| 15,4 m ² = 1 540 dm ²
|
154 km ² = 15 400 000 000 dm ² |
| 0,02 cm ² = 2 mm ²
|
2 024 mm ² = 0,002 024 m ² |
| 3,5 dam ² = 3 500 000 cm ²
|
6 325 cm ² = 0,632 5 .m ² |
Exercice 8 :
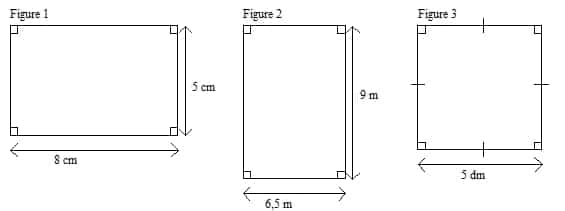
Calculer l’aire des rectangles suivants :
Aire d’un rectangle de manière général est le produit de deux côté consécutifs.
On remarque qu’un carré est un rectangle particulier donc ce qui s’applique plus haut à un rectangle s’applique au carré. Si les longueurs sont en cm, l’aire s’exprimera quant à elle en cm².
Aire(figure1) = 8×5 = 40 cm²
Aire (figure2) = 9×6,5 = 58,5 m²
Aire (figure3) = 5×5 = 25 dm²
Exercice 9 :
L’inscription « 90 g/m² » sur une ramette de papier signifie
que 1 m² de ce papier pèse 90 g.
Combien pèse, en kg, une ramette de 500 feuilles de format A4
(rectangle de 21 cm x 29,7 cm) de ce papier ?
Une feuille a une surface de =0,06237 m²
La ramette de 500 feuilles représente une surface de 0,06237×500=31,185 m²
La masse d’une ramette est de 31,185×90=2806,65 g soit 2,806 kg .
Exercice 10 :
Un triangle d’aire 0,1 dam² a un côté de longueur 800 cm.
Calculer la hauteur relative à ce côté .
0,1 dam²= 10 m² et 800 cm = 8 m .
L’aire est telle que :
Exercice 11 :
Exercice 12 :
a) 2,6 m²=260 dm²=26 000cm²
b) 3 cm² =0,03 dm² = 0,0003 m²
c) 0,574 km² = 57,4 hm²= 574 000 m²
Exercice 14 :
Il y a deux fois les trois quarts d’un disque :
Il y a deux rectangles :
Il y a les trois quarts d’une bande
donc
942,5+400+4,7
Exercice 15 :
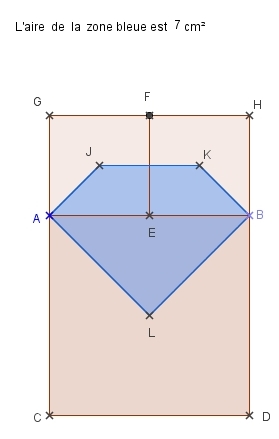
L’aire du grand disque est :
L’aire de cette bonde est :
200-3=197
Exercice 16 :
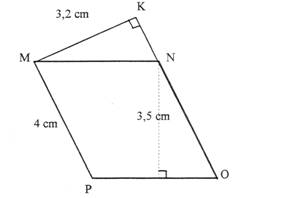
1° Calculer l’aire du parallélogramme MNOP représenté ci-contre.
2° Calculer PO ( arrondir à 0,1 près ).
Exercice 17 :
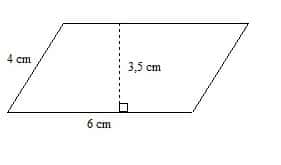
La figure ci-dessous est un parallélogramme
Observons le schéma ci dessous :
1° Calcule son aire.
Sur la figure numéro 2, [AE] est la hauteur relative au côté [DC]. Et l’aire de ABCD est tout simplement le produit de la longueur du côté et de son hauteur relative.
Ici Aire = 6×3,5=21cm²
2. Calculer son périmètre.
Le périmètre est la somme des longueurs des côtés, soit 2xAD+2xAB
Ici Périmètre = 2×4+2×6 = 8+12=20 cm.
Exercice 18 :
La fusée Ariane 5 mesure 57 m de haut.
a) Quelle est la hauteur de sa maquette à l’échelle ?
b) Le diamètre de la maquette est de 5,7 cm. Quel est le diamètre réel de la fusée ?.

Exercice 19 :
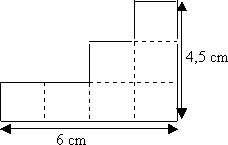
Calculer le périmètre de la figure suivante :
Prenons un seul parallélogramme.
comme il a deux parallélogrammes de part et d’autres.
Le périmètre correspondant à un parallélogramme est :
4+3+(4-3)=4+3+1=8 cm
Il y a 9 parallélogrammes
Le périmètre est donc 9×8 = 72
Exercice 20 :
cm
Exercice 21 :
A – « L’intrus » :
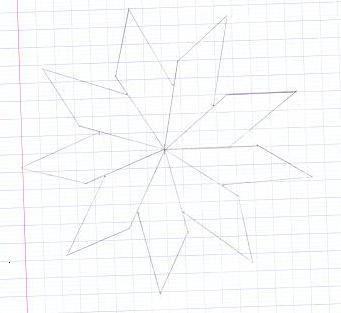
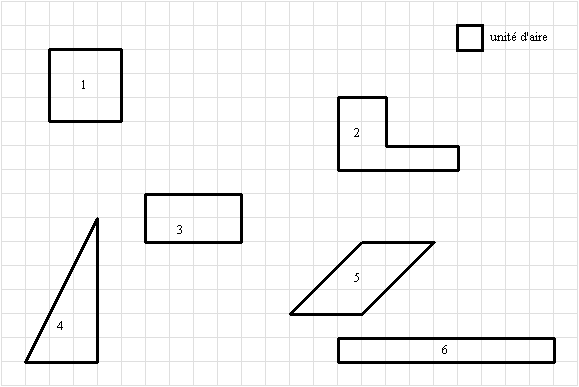
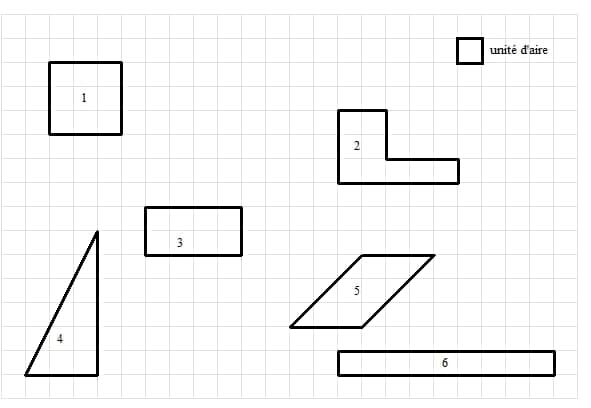
Sur le quadrillage ci-dessous, on a dessiné six figures.
Sachant que l’unité d’aire est le carreau, calculer l’aire de chacune des 6 figures et trouver ainsi l’intrus .
Exercice 22 :
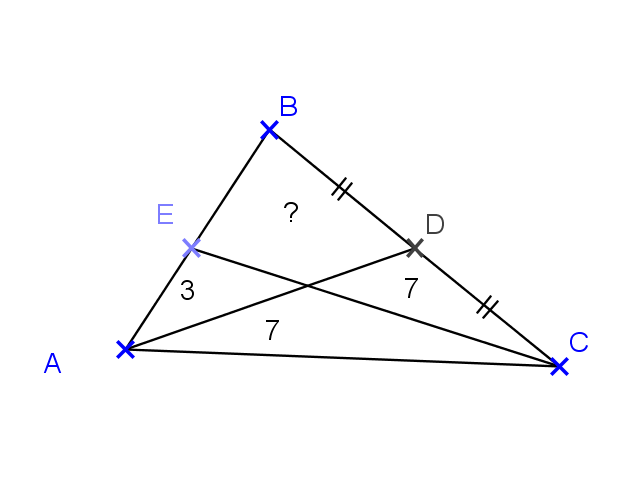
(AD) est une médiane du triangle ABC.
Propriété : la médiane d’un triangle divise, ce triangle, en deux autres triangles de même aire.
donc
donc
Exercice 23 :
Exercice 24 :
Exercice 25 :
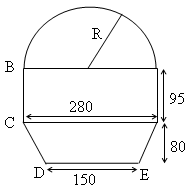
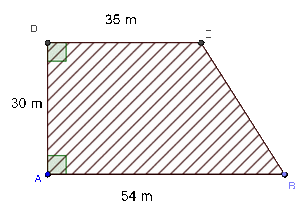
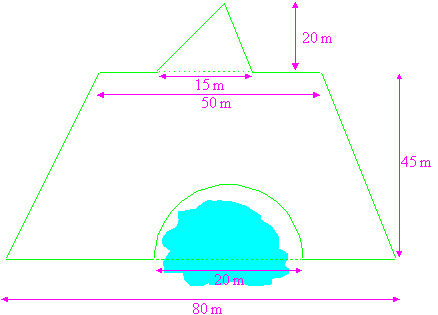
Calculer l’aire du champ suivant en
Cette figure est constituée d’un trapèze rectangle auquel on enlève un demi-cercle, puis on y rajoute un triangle.
L’aire de cette figure est donnée par l’expression numérique suivante :
est la valeur exacte de l’aire du champ.
Une valeur approchée est :
Exercice 27 :
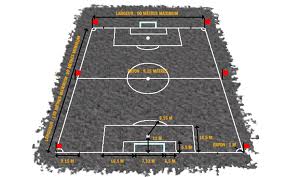
Un terrain de football représenté à l’échelle est un rectangle de 23,1 cm de longueur sur 13,6 cm de largeur.
Quelles sont les dimensions réelles de ce terrain de football ?
Ce n’est pas possible de répondre, il faut la valeur de l’échelle…
Exercice 28 :
Effectuer les conversions :
a. 12m² =1 200 dm² b. 1,32dm² =132 cm²
c. 4,5 cm² =0,00045 m² d. 8 552m²=0,008 552 km²
Les calculs d’aires sont à maîtriser impérativement par les élèves en 5ème. En effet, ce chapitre leur procure de nouvelles compétences en maths. En outre, avec les calculs d’aires et de périmètres en 5ème, vous allez progresser tout au long de l’année scolaire.
Exercice 29 : Pour prendre un bon départ sur les formules d’aires.
A – « L’intrus » : Sur le quadrillage ci-dessous, on a dessiné six figures.
Sachant que l’unité d’aire est le carreau, calcule l’aire de chacune des 6 figures et trouve ainsi l’intrus .
Aire de la figure 1 : 9 u.a ; Aire de la figure 2 : 9 u.a ; Aire de la figure 3 : 8 u.a ;
Aire de la figure 4 :9 u.a ; Aire de la figure 5 : 9 u.a ; Aire de la figure 6 : 9 u.a ;
L’intrus est la figure 3.
B – 1°) Complète:
Aire du rectangle : Aire = Lxl avec L : la longueur l : la largeur
Aire du carré : Aire = cxc = c2 avec c : le côté
2°) Calcule l’aire des figures suivantes:
Figure 1 : Aire = 5×8=40 cm².
Figure 2 : Aire =6,5×9=58,5 cm².
Figure 3 : Aire = 5×5=25 dm².
Exercice 30 : Revoir les UNITES D’AIRE.
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|||||||
|
|
ha |
a |
ca |
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 m² = 100 dm² = 10 000cm² = 1 000 000 mm²
1 m² = 0,01 dam² = 0,000 1 hm² = 0,000 001 km²
ca = 1 m² 1 a = 1 dam² 1 ha = 1 hm²
- Indique une unité appropriée pour exprimer chaque longueur ou chaque aire :
a) la hauteur de la salle de classe : 3 m b) l’étendue d’un champ :300 m
c) la distance Paris – Lyon : 400 km d) la superficie d’une table : 6 m²
e) le périmètre d’un stade : 600 m f) l’aire d’un confetti : 6 mm²
- Complète :
360 cm² = 3,6 dm² 1 km² = 1 000 000 m² 10 000 m² = 1 hm².
8 m² = 800 dm ² = 80 000 cm² .
145 cm² = 0,014 5 m² = 1 450 000 mm²
0,1 dam ² =10 m² = 0,000 01km²
- Complète :
| 15,4 m ² =1 540dm ²
|
154 km ² =15 400 000 000 dm ² |
| 0,02 cm ² = 200 mm ²
|
2 024 mm ² = 0,02024 m ² |
| 3,5 dam ² = 3 500 000 cm ²
|
6 325 cm ² = 0,6325 m ² |
| 4,9 km ² = 4 900 000 m ²
|
3 060 mm ² = 0,306 cm ² |
| 2,74 dm ² =274 cm ²
|
58 830 cm ² = 5,883 m ² |
| 0,68 cm ² =68 mm ²
|
46 000 m ² =0,046 km ² |
| 1 600 m ² =0,001 6 km ²
|
172 mm ² = 1,7 2 cm ² |
| 3 m ² =30 000 cm ²
|
7,2 mm ² =0,072 cm ² |
| 3 ha =300a=3×100=300 m ²
|
18 ha = 18×100 a=800 a=800×100 m²=80 000 m² =800 000 000 cm² |
Exercice 31 :
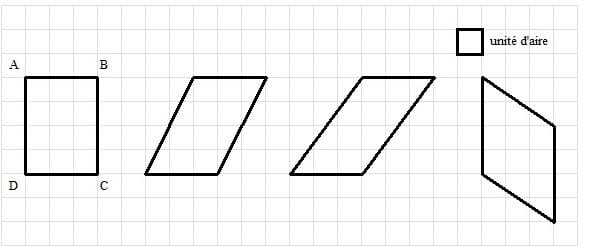
En prenant comme unité d’aire le carreau, donne l’aire du rectangle ABCD puis l’aire de chacun des parallélogrammes.
3×4=12 3×4=12 3×4=12 4×3 = 12
Exercice 32 :
La figure ci-dessous est un parallélogramme.
1° Calculer son aire.
6×3,5=21 cm²
2° Calculer son périmètre.
2x(4+6)=20 cm
Exercice 33 :
On considère le parallélogramme ci-dessous.
( a et d désignent les hauteurs ) .
Entourer les produits qui expriment l’aire de ce parallélogramme ?
|
a |
c |
b |
a |
a |
b |
Exercice 34 :
Compléter le tableau suivant, où c désigne un côté de parallélogramme, h la hauteur relative à ce côté, et A l’aire du parallélogramme:
|
c |
h |
A |
|
7,3 cm |
5,4 cm |
39,42 cm² |
|
225 m |
2 dam |
4,5 dam2 |
|
5 m |
2,3 m |
11,5 m2 |
|
… m |
15 cm |
4,5 m2 |