Représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.
Mis à jour le 5 août 2025
Exercice 1 :
Dans un repère orthonormé de l’espace, 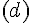 et
et 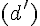 sont les droites de représentations paramétriques
sont les droites de représentations paramétriques
respectives :
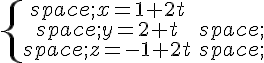
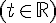
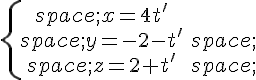
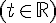
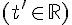
a) Montrer que les droites 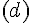 et
et 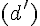 ne sont pas parallèles.
ne sont pas parallèles.
b) Étudier l’intersection de 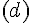 et
et 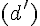 en résolvant un système d’équations.
en résolvant un système d’équations.
Exercice 2 :
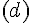 et
et 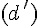 sont deux droites de représentations paramétriques respectives :
sont deux droites de représentations paramétriques respectives :
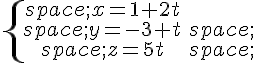
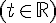
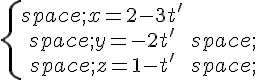
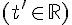
Indiquer oralement les coordonnées d’un point et d’un vecteur directeur de chacune des droites 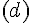 et
et 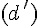 .
.
Exercice 3 :
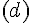 est la droite de représentation paramétrique :
est la droite de représentation paramétrique :
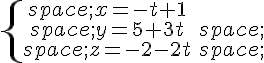
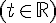
Déterminer mentalement les coordonnées de quatre points de la droite 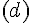 .
.
Exercice 4 :
On donne les points :
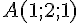 et
et 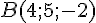
Parmi ces systèmes, une représentation paramétrique de la droite (AB) est :
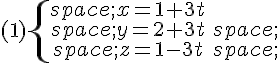
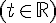
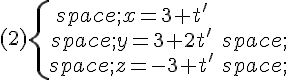
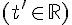
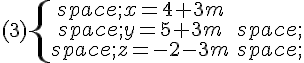
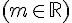
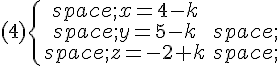
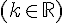
Exercice 5 :
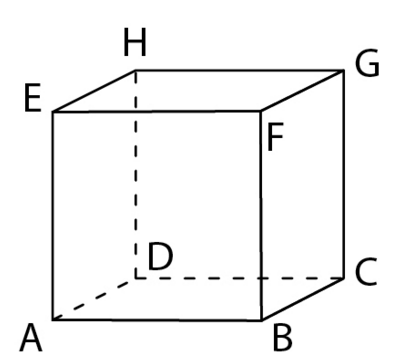
ABCDEFGH est le cube représenté ci-dessous.
a) Déterminer les coordonnées de chacun des sommets dans le repère 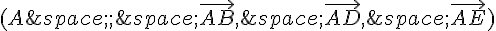 .
.
b) Déterminer une représentation paramétrique de chacune des droites (AG) et (BH).
Exercice 6 :
ABCDEFGH est le cube représenté ci-contre.
Pour chacun des plans ci-dessous, indiquer oralement deux vecteurs normaux.
a) (ABC)
b) (BCF)
c) (ADF)
Exercice 7 :
Déterminer une équation cartésienne du plan :
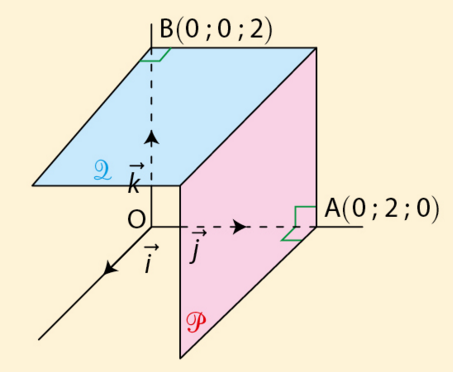
a) 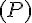 coloré en rouge passant par le point A et orthogonal à l’axe des ordonnées ;
coloré en rouge passant par le point A et orthogonal à l’axe des ordonnées ;
b) 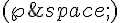 coloré en bleu passant par le point B et orthogonal à l’axe des côtes.
coloré en bleu passant par le point B et orthogonal à l’axe des côtes.
Exercice 8 :
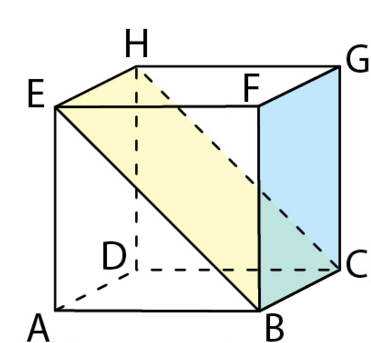
On se place dans le repère orthonormé 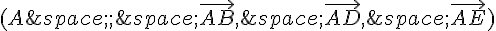 .
.
a) Déterminer les coordonnées d’un vecteur normal au plan (BCF), puis au plan (BCE).
b) Déterminer une équation cartésienne du plan (BCF), puis du plan (BCE).
Exercice 9 :
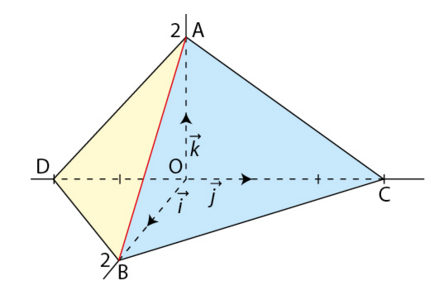
On a placé quatre points A, B, C, D dans le repère orthonormé ci-dessous.
a) Lire les coordonnées des points A, B, C, D.
b) Démontrer que le vecteur 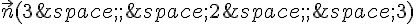 est normal au plan (ABC) ; puis que le vecteur
est normal au plan (ABC) ; puis que le vecteur 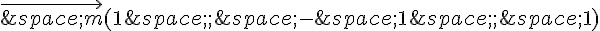 est normal au plan (ABD).
est normal au plan (ABD).
c) Déterminer une équation cartésienne du plan (ABC), puis du plan (ABD).
d) Alix affirme « Le point 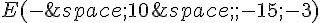 appartient à l’un des deux plans ».
appartient à l’un des deux plans ».
A-t-elle raison ?
Exercice 10 :
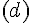 et
et 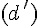 sont les droites de représentations paramétriques respectives :
sont les droites de représentations paramétriques respectives :
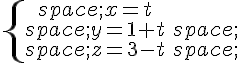
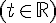 et
et 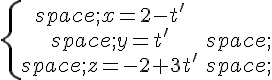
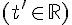
Déterminer mentalement lequel de ces systèmes on est amené à résoudre pour déterminer l’inter
section de 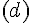 et
et 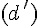 .
.
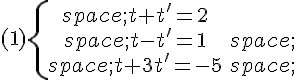 et
et 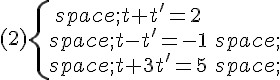
Exercice 11 :
Voici les représentations paramétriques respectives de deux droites 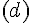 et
et 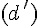 sécantes.
sécantes.
Déterminer leur point d’intersection.
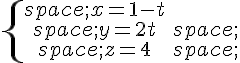
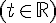 et
et 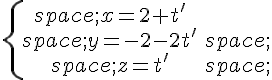
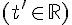
Exercice 12 :
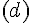 et
et 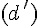 sont les droites de représentations paramétriques respectives :
sont les droites de représentations paramétriques respectives :
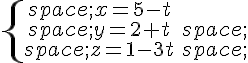
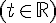 et
et 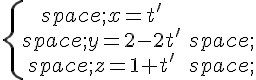
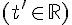
a) Démontrer que 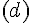 et
et 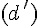 ne sont pas parallèles.
ne sont pas parallèles.
b) Démontrer que 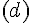 et
et 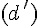 ne sont pas coplanaires en résolvant un système d’équations.
ne sont pas coplanaires en résolvant un système d’équations.
Exercice 13 :
a et b désignent des nombres réels.
On donne les points 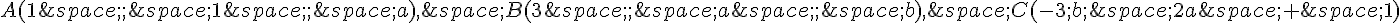 .
.
On se propose de déterminer a et b afin que les points A, B, C soient alignés.
a) Déterminer les coordonnées des vecteurs 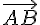 et
et 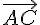 .
.
b) Montrer que les points A, B, C sont alignés si, et seulement si,
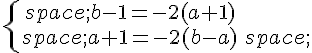
c) Résoudre ce système et conclure en donnant les coordonnées de A, B, C.
Exercice 14 :
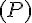 est un plan d’équation cartésienne :
est un plan d’équation cartésienne :
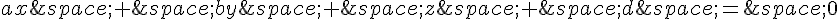 (avec a et b nombres réels).
(avec a et b nombres réels).
Existe-t-il des nombres a et b tels que les points 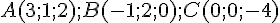 appartiennent
appartiennent
au plan 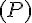 .
.
Exercice 15 :
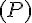 est le plan d’équation cartésienne :
est le plan d’équation cartésienne :
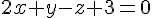 .
.
A est le point de coordonnées 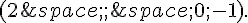
a) Déterminer une représentation paramétrique de la droite 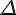 passant par A et perpendiculaire au plan
passant par A et perpendiculaire au plan 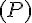 .
.
b) En déduire les coordonnées du point H, projeté orthogonal du point A sur le plan 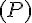 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.