Exercice 17 :

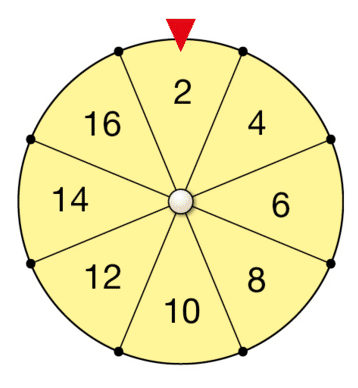
L’événement E : « Le numéro repéré est divisible par 4 » signifie que les numéros 4 ou 8 seront obtenus. L’événement contraire signifie que les numéros 1, 2, 3, 5, 6 ou 7 seront obtenus.

Dans le cas de la roue équilibrée, chaque secteur a la même probabilité d’être sélectionné lors du tirage. Comme il y a deux secteurs qui correspondent à l’événement E et six secteurs qui correspondent à l’événement contraire, la probabilité d’obtenir un numéro divisible par 4 est 2/8 = 1/4, et la probabilité d’obtenir un numéro non divisible par 4 est 6/8 = 3/4.
Ainsi, les événements E et son contraire ont la même probabilité, car ils correspondent à des issues équiprobables sur la roue.

Exercice 18 :

1.
a. Les issues qui réalisent l’événement E_1: 2, 4, 6, 8
b. Les issues qui réalisent l’événement E_2: 4, 5, 6, 7, 8
c. Les issues qui réalisent l’événement E_3: 4, 6, 8

2.
a. P(E_1) = 4/8 = 1/2 = 0,5
b. P(E_2) = 5/8 = 0,625
c. P(E_3) = 3/8 = 0,375

Exercice 19 :

1.
a. L’expérience compte 32 issues, une pour chaque carte dans le jeu de 32 cartes.
b. Chaque issue a une probabilité de 1/32 car chaque carte a la même probabilité d’être tirée.

2.
a. Les issues qui réalisent l’événement E (carte tirée est rouge) sont les cartes cœur et carreau.
Les issues qui réalisent l’événement F (carte tirée est un as) sont les cartes as de trèfle, as de pique, as de cœur et as de carreau.

b. La probabilité de l’événement E est de 16/32 = 1/2 car il y a 16 cartes rouges dans le jeu.
La probabilité de l’événement F est de 4/32 = 1/8 car il y a 4 as dans le jeu.

3. Les cartes qui réalisent les deux événements E et F en même temps sont les deux as rouges: l’as de cœur et l’as de carreau.

Exercice 20 :

1.

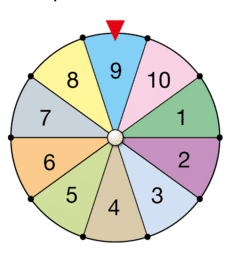
Les issues qui réalisent l’événement E (numéro pair) sont : 2, 4, 6, 8, 10.
Les issues qui réalisent l’événement F (multiple de 3) sont : 3, 6, 9.
Les issues qui réalisent l’événement G (multiple de 5) sont : 5, 10.

2.

a. Les événements E (numéro pair) et F (multiple de 3) ne sont pas incompatibles car l’issue 6 les satisfait toutes les deux.
b. Les événements E (numéro pair) et G (multiple de 5) sont incompatibles car aucun numéro satisfait les deux critères.
c. Les événements F (multiple de 3) et G (multiple de 5) sont incompatibles car il n’y a pas de numéro qui soit à la fois multiple de 3 et de 5.

3.

La probabilité de l’événement E est de 5/10 = 1/2.
La probabilité de l’événement F est de 3/10.
La probabilité de l’événement G est de 2/10 = 1/5.

Exercice 21 :

1.
a. L’arbre de probabilité est à compléter en fonction des probabilités des issues pour chaque étape.
b. L’expérience compte 10 issues au total.

2.
La probabilité d’obtenir la couleur rouge est de 2/10 = 1/5.
La probabilité de ne pas obtenir la couleur jaune est de 4/5.

Exercice 22 :

a. L’arbre des issues pondéré par les probabilités est à dessiner en fonction des lettres sur les boules et de leurs probabilités.
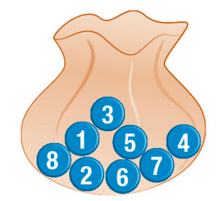
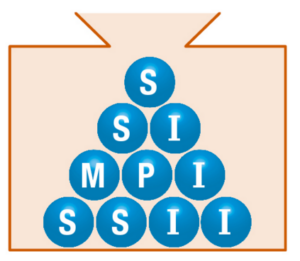
b. Pour calculer la probabilité de l’événement E (la lettre obtenue n’est pas une voyelle), il faut compter le nombre de lettres non voyelles sur les boules (M, S et P) qui est de 3 sur 10, donc la probabilité est de 3/10.

Exercice 23 :

a. L’arbre des issues pondéré par les probabilités est à dessiner en fonction des types de boissons et de leurs quantités.
b. Pour calculer la probabilité de l’événement E (la bouteille n’est pas une bouteille d’eau gazeuse), il faut compter le nombre de bouteilles qui ne sont pas d’eau gazeuse (T, J et S) qui est de 80 sur 120, donc la probabilité est de 80/120 = 2/3.

Exercice 24 :

Les issues qui réalisent l’événement E (Tania lit un nombre pair) sont les numéros 2, 4 et 6.
Les issues qui réalisent l’événement contraire de E sont les numéros 1, 3 et 5.

Exercice 25 :

L’événement contraire de E (obtenir au moins une fois Pile) est l’événement de ne jamais obtenir Pile sur les deux lancers. Donc les issues qui réalisent l’événement contraire de E sont Face-Face.