Les limites et les asymptotes : cours de maths en terminale en PDF.
Mis à jour le 1 septembre 2025
Connaissances nécessaires à ce chapitre :


de deux suites.

pour déterminer une limite de suite.

I.Limite d’une fonction en l’infini
Dans toute cette partie,  désigne la courbe représentative de la fonction f dans un repère quelconque du plan.
désigne la courbe représentative de la fonction f dans un repère quelconque du plan.
1. Limite finie en l’infini
 du type
du type ![]a\,;\,+\infty[](https://mathovore.fr/latex-images/3dbf3b86fea185576956037434e380d3.png) .
.La fonction f a pour limite ℓ en
 si tout intervalle ouvert contenant ℓ contient toutes les
si tout intervalle ouvert contenant ℓ contient toutes lesvaleurs de f (x) pour x assez grand. On note alors :
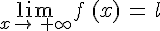 .
.Exemple :
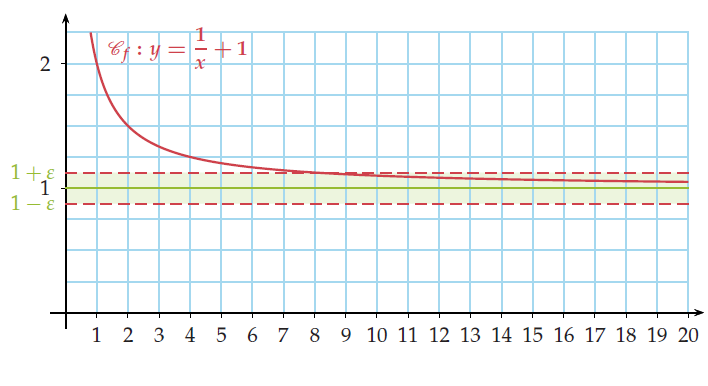
Soit f la fonction définie sur ![]0\,;\,+\infty[](https://mathovore.fr/latex-images/165089428595bbef928ed4c9263743ae.png) par
par 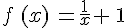 . On a
. On a 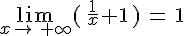 .
.
En effet, l’inverse de x se rapproche de 0 à mesure que x augmente.
Soit un intervalle ouvert I tel que 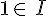 . Alors, f (x) sera toujours dans I pour x assez grand.
. Alors, f (x) sera toujours dans I pour x assez grand.
Graphiquement, aussi étroite que soit une bande parallèle à la droite d’équation y = 1 et qui la
contient, il existe toujours une valeur de x au delà de laquelle  ne sort plus de cette bande.
ne sort plus de cette bande.
 en
en  si
si 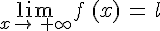 .
.Remarque :
On définit de façon analogue 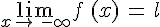 qui caractérise une asymptote horizontale à
qui caractérise une asymptote horizontale à  en
en 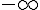 d’équation y = ℓ.
d’équation y = ℓ.
Exemple :
On a vu précédemment que 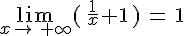 . On a aussi
. On a aussi 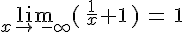 .
.
Donc, la droite d’équation y = 1 est asymptote horizontale à la courbe  en
en  et en
et en 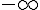 .
.
 .
.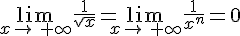 et
et 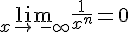 .
.II. Limite infinie en l’infini
 en
en  si tout intervalle de
si tout intervalle de  du type
du type ![]a\,;\,+\infty[](https://mathovore.fr/latex-images/3dbf3b86fea185576956037434e380d3.png) contient
contienttoutes les valeurs de f (x) pour x assez grand. On note alors :
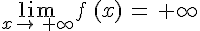 .
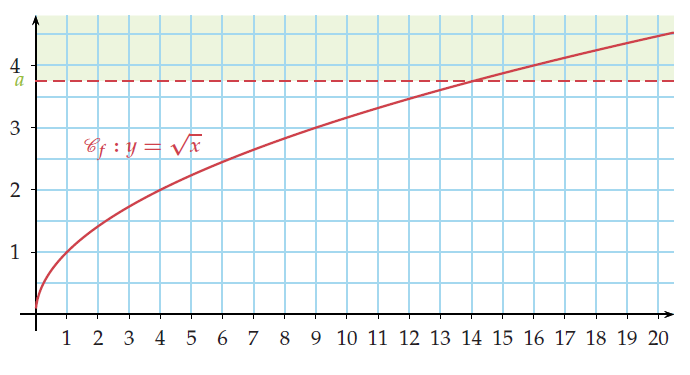
.Exemple :
Soit f la fonction racine carrée. On a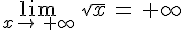 .
.
En effet, 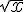 devient aussi grand que l’on veut à mesure que x augmente.
devient aussi grand que l’on veut à mesure que x augmente.
Soit un intervalle ouvert ![I\,=]a\,;\,+\infty[](https://mathovore.fr/latex-images/906de02a1ad6456988496e6fde9fb569.png) . Alors, f (x) sera toujours dans I pour x assez grand.
. Alors, f (x) sera toujours dans I pour x assez grand.
Graphiquement, si on considère le demi-plan supérieur de frontière une droite d’équation
y = a, il existe toujours une valeur de a au-delà de laquelle  ne sort plus de ce demi-plan.
ne sort plus de ce demi-plan.
 .
.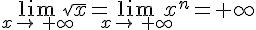 et
et 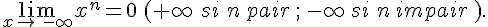
2. Limite infinie en un réel
 du type
du type ![]x_0\,-\varepsilon\,;\,x_0[](https://mathovore.fr/latex-images/a6d4ed444c063b819cd363ccd5e32403.png) ou
ou ![]x_0\,;\,x_0+\varepsilon[](https://mathovore.fr/latex-images/6966206f6fec8ee0045dce4041cb08d1.png) .
.La fonction f a pour limite
 en
en  si tout intervalle de
si tout intervalle de  du type
du type ![]A\,;\,+\infty[](https://mathovore.fr/latex-images/c660f7eba3b1d5122284fdb9c4dbcccc.png) contient toutes
contient toutesles valeurs de f (x) pour x assez proche de
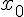 . On note alors :
. On note alors : 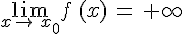 .
.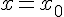 est asymptote verticale à
est asymptote verticale à  si
si 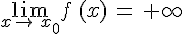 ou
ou 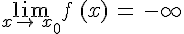 .
.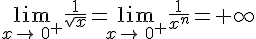 et
et 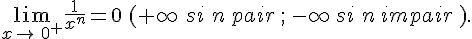
III. Opérations sur les limites.
IV. Limite d’une fonction composée
1. Fonction composée
La composée de f suivie de g est la fonction notée
 définie sur E par
définie sur E par 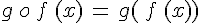 .
.Remarque :
Il ne faut pas confondre  et
et 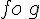 qui sont, en général, différentes.
qui sont, en général, différentes.
2. Théorème de composition des limites
 .
.Si
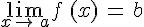 et
et 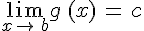 , alors
, alors 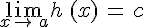 .
.V. Limites et comparaison
1. Théorème de comparaison
2. Théorème d’encadrement dit « des gendarmes » ou « sandwich ».
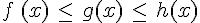 .
.Si
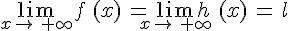 , alors
, alors 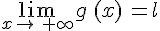 .
.Remarque :
On a, comme pour le théorème de comparaison précédent, deux théorèmes
analogues lorsque x tend vers − et lorsque x tend vers un réel
et lorsque x tend vers un réel 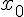 .
.
Exemple :
Déterminons la limite en − de
de 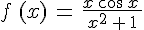 .
.
La limite de cos x en − est indéterminée. Donc celle de f (x) aussi.
est indéterminée. Donc celle de f (x) aussi.
Cependant pour tout x réel strictement négatif, 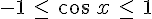 donc
donc 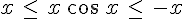 .
.
Et en divisant membre à membre par 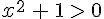 on a :
on a :
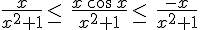 .
.
Pour 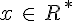 ,
,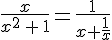 .
.
Or, 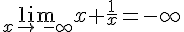 donc
donc 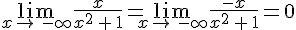
Donc, d’après le théorème des gendarmes,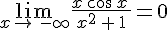 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les limites et les asymptotes : cours de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.























