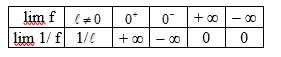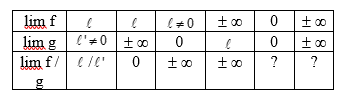Limites et asymptotes : cours de maths en 1ère en PDF.
Mis à jour le 25 août 2025
Les tableaux ci-dessous résument les résultats à connaître.
Ces tableaux sont valables dans les trois situations étudiées:
- Lorsque la variable
.
- Lorsque la variable
.
- Lorsque la variable
où a
R.
Mais il va de soi que, pour les deux fonctions f et g concernées, les limites sont prises au même endroit!
Dans le cas particulier où les fonctions sont des suites numériques, on peut utiliser ces résultats en remplaçant f par (Un) et g par (Vn) avec le seul cas envisageable la variable .
Les conventions utilisées dans ces tableaux, sont:
· et
désignent des nombres réels ( limites finies ).
· ? indique que dans la situation concernée, on n’a pas de conclusion générale.
On dit parfois qu’il s’agit d’une « forme indéterminée » notée F.I.
Il faudra dans ces cas, mettre au point d’autres méthodes de résolution.
I. Limite d’une somme de deux fonctions
II. Limite d’une différence de deux fonctions
Utiliser : f – g = f + (-g) et le tableau précédent.
III. Limite d’un produit de deux fonctions
IV. Limite de l’inverse d’une fonction
Dans le tableau ci-dessous, la limite de f égale à , signifie, qu’à l’endroit où la limite est prise, cette limite est zéro et que, pour tout x suffisamment proche de cet endroit, on a f(x) > 0.
Définition analogue pour , mais avec f(x) < 0.
V. Limite d’un quotient de deux fonctions
On peut utiliser: et avec les deux tableaux précédents, il est possible de conclure.
En + ou en –
, la limite d’une fonction rationnelle est la limite du quotient des termes de plus haut degré du numérateur et du dénominateur.
On peut aussi retenir les résultats suivants :
Ce tableau est simplifié: ± signifie +
ou bien –
.
Pour décider, on applique la règle du signe du quotient selon les signes de f et de g au voisinage de l’endroit où la limite est cherchée.
VI. Limite des fonctions de références.
VII. Le théorèmes de comparaison
Pour les fonctions, dans les propriétés ci-dessous, la lettre a désigne aussi bien un réel que + ou –
.
Lorsque a = + , les fonctions sont définies sur R ou un intervalle I de la forme [ A ; +
[ où A est un réel.
Lorsque a = – , les fonctions sont définies sur R ou un intervalle I de la forme ] –
; A ] où A est un réel.
Lorsque a R , les fonctions sont définies sur R ou un intervalle I de la forme [ A ; B ] où A et B sont des réels et a
[ A ; B ].
Si la limite concernée est la limite à gauche de a, les fonctions sont définies sur un intervalle I de la forme ] – ; a [ ou [ A ; a [ où A est un réel.
Si la limite concernée est la limite à droite de a, les fonctions sont définies sur un intervalle I de la forme ] a ; + [ ou ] a ; A ] où A est un réel.
Pour les suites, l’indice n est un entier naturel supérieur ou égal à un certain rang (qui sera souvent 0).
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «limites et asymptotes : cours de maths en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
