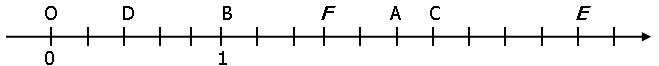I. Les nombres décimaux
- Il existe dix CHIFFRES : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
- Un MOT s’écrit avec des lettres.
- Un NOMBRE s’écrit avec des chiffres.
1.Ecriture de position :
Tout nombre décimal peut s’écrire en deux parties séparées par une virgule :
La partie entière suivie de la virgule suivie de la partie décimale.
Suivant sa position, un chiffre indique :
- les unités, les dizaines, les centaines . . . dans la partie entière.
- les dixièmes, les centièmes, les millièmes . . . dans la partie décimale.
Partie entière |
Partie decimale |
millier |
centaine |
dizaine |
unité |
dixième |
centième |
millième |
7 |
4 |
2 |
5 |
6 |
3 |
Exemple :
La partie entière est 742 et la partie décimale est 563.
7 centaines , 4 dizaines , 2 unités , 5 dixièmes , 6 centièmes , 3 millièmes.
Exemples :
- Dans le nombre 5,63 le chiffre 6 est le chiffre des dixième.
- Dans le nombre 917,842 le chiffre des centièmes est 4 et chiffre des unités est 7
- Dans le nombre 1,976 le chiffre 6 est le chiffre des millièmes et 9 est le chiffre des dixièmes.
2. Les zéros utiles et inutiles :
On peut écrire ou supprimer des zéros à gauche de la partie entière ou à droite de la partie décimale.
Cela ne change pas sa valeur.
Ainsi
Un nombre entier est aussi un nombre décimal car 37 = 37,0 .
Exemples :
a. En supprimant les zéros inutiles si cela est possible, complète les égalités :
b. Complète par = ou
3- Les écritures d’un nombre
3.1. Ecriture avec des lettres :
- Million et Milliard sont des noms, ils prennent un s au pluriel.
- Vingt et Cent prennent un s au pluriel s’ils ne sont pas suivis d’un autre nombre.
- Mille est invariable, il ne prend jamais de s au pluriel.
Exemples :
Ecrire en lettres les nombres suivants :
600 : six cents.
540 : cinq cent quarante.
287 : deux cents quatre vingt sept.
80 : quatre-vingts ;
7,03 : sept et trois centièmes .
2 005 076 : deux millions et cinq mille et soixante seize.
3.2. Ecriture avec des fractions décimales :
Un nombre décimal a plusieurs écritures.
Exemple :
(c’est l’écriture fractionnaire de 237,45).
Application :
Donne l’écriture décimale ou/et l’écriture fractionnaire des nombres suivants :
.
4. La droite graduée :
Pour graduer une droite, on choisit : un sens , une origine O et une unité de longueur.
On repère chaque point d’une droite graduée par un nombre appelé l’abscisse.
On dit que 2 est l’abscisse du point A ou que le point A a pour abscisse 2. On note A( 2 )
Exemples :
L’abscisse de B est 1 . L’abscisse de C est 2,2 . L’abscisse de D est 0,4 .
Sur cette droite graduée, place les points .
II. Ordre des nombres décimaux :
1. Comparaison des nombres décimaux :
Comparer deux nombres décimaux, c’est dire lequel est le plus grand, le plus petit ou s’ils sont égaux :
- « > » signifie « est supérieur à » ( est plus grand que ) ;
- « < » signifie « est inférieur à » ( est plus petit que ) .
Cas 1 : les parties entières sont différentes.
On compare les parties entières ;
57,235 est inférieur à 71,12
Cas 2 : les parties entières sont égales.
1ère méthode : On compare les décimales de même rang 7,267 < 7,293
2ème méthode : On essaye d’obtenir le même nombres de décimales 7,293 > 7,291
Remarque :
Le nombre qui a le plus de chiffres n’est pas toujours le plus grand 5,9 > 5,899
Exemple :
Comparer les nombres décimaux suivants :
.
- Classer des nombres par ordre croissant, c’est les ranger du plus petit au plus grand ;
- Classer des nombres par ordre décroissant, c’est les ranger du plus grand au plus petit.
Exemples :
Ranger dans l’ordre croissant les nombres décimaux suivants :
Réponse :
2. Intercaler et Encadrer :
Entre deux nombres décimaux, on peut toujours intercaler un nombre décimal.
Exemple :
Comparer
Voici des encadrements de 13,71 :
10 < 13,71 < 20 10 < 13,71 < 15 13 < 13,71 < 14
(ici, 13,71 est encadré par 2 entiers consécutifs)
3. Tronquer et arrondir :
La troncature à l’unité d’un nombre décimal est sa partie entière .
Exemple :
La troncature de à l’unité est
.
L’arrondi à l’unité d’un nombre décimal est le nombre entier le plus proche :C’est le nombre entier précédent si le chiffre des dixièmes est 0 , 1 , 2 , 3 ou 4;
C’est le nombre entier suivant si le chiffre des dixièmes est 5 , 6 , 7 , 8 ou 9.
Exemple :
L’arrondi à l’unité de 27,32 est 27 ;
l’arrondi à l’unité de 37,8 est 38.
L’arrondi à l’unité de 72,583 est 73.
| 36,89 | 504,36 | 29,654 | 324,507 | |
| Troncature au dixième | 36,8 | 504,3 | 29,6 | 324,5 |
| Arrondi au dixième | 36,9 | 504,4 | 29,7 | 324,5 |
III. Multiplier ou diviser par 10 , 100 ou 1000
1. Règle de calcul :
Multiplier par 10, 100 ou 1000 revient à déplacer la virgule vers la
droite, d’autant de rang qu’il y a de zéro(s), en plaçant un ou des zéros si c’est nécessaire.
Exemples :
Diviser par 10, 100 ou 1000 revient à déplacer la virgule d’un, deux ou trois rangs vers la gauche en plaçant un ou des zéros si c’est nécessaire.
Exemples :
Vous avez assimilé le cours sur les nombres décimaux en 6ème ?
Effectuez ce QCM de maths en sixième sur les nombres décimaux afin d’évaluer vos acquis sur cette leçon.
Quizz sur les nombres entiers et les nombres décimaux en sixième.