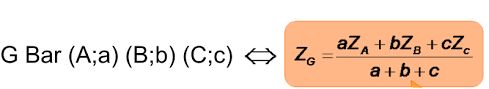Nombres complexes : cours de maths en terminale en PDF.
I. Notion de nombre complexe :
1. Théorème :
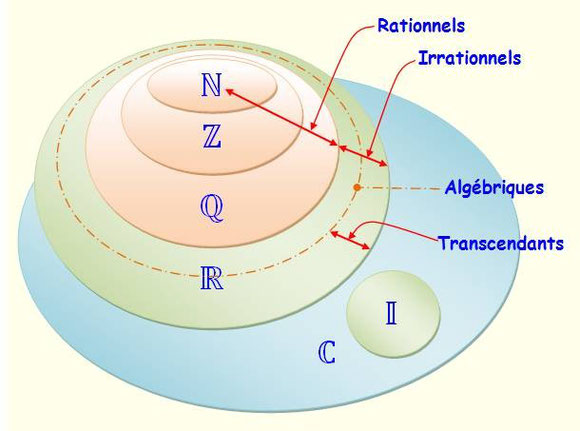
Il existe un ensemble noté , appelé ensemble des nombres complexes qui possède les propriétés suivantes :
contient l’ensemble des nombres réels;
- L’addition et la multiplication des nombres réels se prolongent aux nombres complexes et les règles de calcul restent les mêmes.
- Il existe un nombre complexe noté i tel que
;
- Tout nombre complexe
s’écrit de manière unique
avec
et
réels.
Exemple :
z =3 + 5i ; z = – 3,7i ; z = – 7i sont des nombres complexes.
Un peu d’histoire :
En 1777, Euler introduit la lettre i, Gauss en généralisera l’emploi à partir de 1830.
2. Définition :
L’écriture z = x+iy avec x et y réels est appelée forme algébrique du nombre complexe z .
x est la partie réelle de z, notée Re(z).
y est la partie imaginaire de z, notée Im(z) .
Exemple :
z = -3 +5i alors Re(z) = -3 et Im(z) = 5
Remarque :
- Les parties réelles et imaginaires sont des nombres réels.
- Lorsque y=0, z est un réel et lorsque x=0, z= iy (y réel) est appelé imaginaire pur.
3. Propriété 1 :
Deux nombres complexes sont égaux si et seulement si, ils ont même partie réelle et même partie imaginaire.
Remarque :
- Cette propriété découle de l’unicité de l’écriture d’un nombre complexe sous forme algébrique.
- En particulier, x et y étant des réels,
si et seulement si
et
.
II. Représentation géométrique des nombres complexes.
Soit un repère orthonormé du plan .
1. Définition.
A tout nombre complexe avec
et
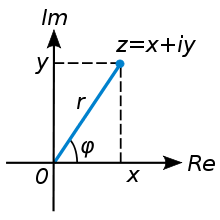
réels, on associe le point M de coordonnées
.
On dit que
- M est le point image de z
- OM est le vecteur image de z.
- z est l’affixe du point M on note M(z)
Le plan est alors appelé plan complexe, noté P.
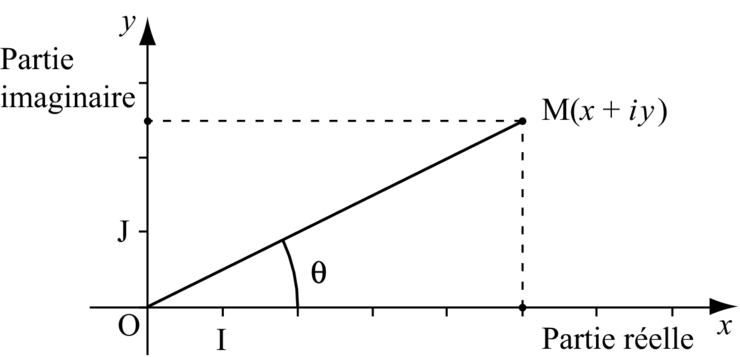
Remarque et vocabulaire :
- Les nombres réels sont les affixes des points de l’axe des abscisses appelé axe des réels .
- Les imaginaires purs sont les affixes des points de l’axe des ordonnées appelé aussi axe des imaginaires purs.
[2pi], on dit que
est un repère direct .
III. Opérations sur les nombres complexes :
1. Addition et multiplication dans C :
1.1. Règles de calculs :
L’addition et la multiplication des nombres réels se prolonge aux nombres complexes et les règles de calcul restent les mêmes.
Exemple :
(car i² = – 1) .
Remarque :
- Les identités remarquables abordées en classe de 3° restent valables dans
- Soit z et z’ éléments de C,
équivaut à
ou
.
1.2. Représentations géométrique de la somme.
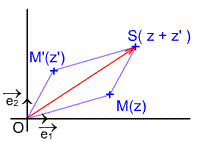
Deux nombres complexes et
ont pour images respectives M et M’ dans le plan complexe .
a pour image le point S quatrième sommet du parallélogramme OMSM’ .
2. Inverse et quotient :
2.1. Propriété 2 :
Tout nombre complexe non nul z admet un inverse noté .
Pour obtenir la forme algébrique de :
((x,y) différent du couple (0;0)).
On multiplie numériquement le numérateur et le dénominateur par car
est un nombre réel.
L’avantage est de faire disparaître le i au dénominateur.
Exemples :
Ecrire sous forme algébrique et
.
3. Affixe d’un vecteur, d’un barycentre :
3.1. Propriété 3 :
Deux points A et B du plan complexe ont pour affixes respectives et
.
L’affixe du vecteur est
.
Remarques :
- Deux vecteurs sont égaux si et seulement si leurs affixes sont égales.
- Si k est un réel, l’affixe du vecteur
est
où z est l’affixe de
.
3.2. Propriété 4 :
Deux points A et B du plan complexe ont pour affixes respectives et
.
L’affixe du barycentre G des points pondérés et
(avec
non nul) est :
.
Remarque :
Ce résultat se généralise à plus de deux points.
Vous avez assimilé ce cours sur les nombres complexes en terminale ?
Effectuez ce QCM sur les nombres complexes en classe de terminale.
Un QCM sur les nombres complexes