Sommaire

🧮Cours de Mathématiques

Terminale • Lycée

La fonction logarithme népérien

📖 Temps de lecture : 5 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

La fonction logarithme népérien avec un cours de maths en terminale faisant intervenir la définition du logarithme et ses propriétés.

I. Définition de la fonction logarithme népérien :

Définition :

Pour tout réel $x$ de $]0;+\infty[$ , il existe un unique réel y tel que $e^y=x$ .

Définition :

La fonction logarithme népérien, notée ln, est la fonction définie sur ]0 ; $+\infty$ [ qui à tout réel x>0, associe le réel noté ln(x) dont l’exponentielle est x.

Remarque :

L’image d’un réel strictement positif x par la fonction ln se note souvent ln x au lieu de ln(x).

Conséquences :

1. Pour tout réel x>0 et tout réel y, $x=e^y$ équivaut à $y=lnx$ .

2. Pour tout réel x>0, $e^{lnx}=x$ .

3. Pour tout réel x, $ln(e^x)=x$

Preuve :

(1) et (2) se déduisent directement de la définition.

(3) Pour tout réel x, si y= $ln(e^x)$ alors d’après (1) $e^x=e^y$ donc x=y.

Conséquences :

$ln1=0$ .En effet $e^0=1$ et d’après (1) ceci équivaut à $ln1=0$ .

$lne=1$ .En effet $e^1=e$ et d’après (1) ceci équivaut à $lne=1$ .

Pour tout réel $\lambda$ , l’équation $lnx=\lambda$ a pour unique solution $x=e^{ \lambda }$ d’après (1).

Propriété:

Dans un repère orthonormal, les courbes représentatives des fonctions exponentielles et logarithmes népérien sont symétriques par rapport à la droite d’équation y=x.

Preuve :

ON note $\varphi$ et $\varphi ^'$ les courbes représentatives des fonctions exp et ln.

Dire que $M'(x;y)$ appartient à $\varphi ^'$ équivaut à dire que $M(y;x)$ appartient à $\varphi$ .

$\varphi$ et $\varphi ^'$ sont donc symétriques par rapport à la droite y=x.

II. Sens de variation de la fonction logarithme népérien sur 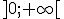$]0;+\infty[$ :

Propriété :

La fonction logarithme népérien est strictement croissante sur $]0;+\infty[$ .

Preuve :

a et b sont deux réels tels que $0<a<b$ , c’est à dire que $e^{lna}<e^{lnb}$ .

La fonction exponentielle est strictement croissante sur $\mathbb{R}$ donc $lna<lnb$ .

Conséquences :

Pour tous réels a et b de $]0;+\infty[$ :

$lna=lnb$ équivaut à $a=b$ et $lna<lnb$ équivaut à $a<b$ .
$lna>0$ équivaut à $a>1$ et $lna<0$ équivaut à $0<a<1$ .

III. Les propriétés algébriques :

1. Relation fonctionnelle :

Théorème :

Pour tout réels a et b de $]0;+\infty[$ , $ln(ab)=lna+lnb$ .

Preuve :

a et b sont deux réels strictement positifs.On note A=lnab et B=ln a + ln b alors

$e^A=ab$ et $e^B=e^{lna+lnb}=e^{lna}\times e^{lnb}=ab$

donc $e^A=e^B$ d’où A=B puisque la fonction exponentielle est bijective sur $\mathbb{R}$ .

2. Logarithme d’un quotient :

Propriété :

Pour tout réel a de $]0;+\infty[$ , $ln\left ( \frac{1}{a} \right )=-lna$ .

Preuve :

Pour a>0, on écrit $a\times \frac{1}{a}=1$ donc $ln(a\times \frac{1}{a})=ln1$

c’est à dire $ln(a)+ln(\frac{1}{a})=0$ d’où $ln(\frac{1}{a})=-ln(a)$ .

Propriété :

Pour tous réels a et b de $]0;+\infty[$ , $ln(\frac{a}{b})=ln(a)-ln(b)$ .

Preuve :

Pour a>0 et b>0, $ln(\frac{a}{b})=ln(a\times \frac{1}{b})=lna+ln\frac{1}{b}=ln(a)-ln(b)$ .

3. Logarithme d’un produit de nombres réels strictement positifs :

Propriété :

Pour tous réels $a_1,a_2,a_3,....,a_n$ de $]0;+\infty[$ ,

$ln(a_1a_2a_3....a_n)=lna_1+lna_2+lna_3+....+lna_n$

Remarque :

Cette formule généralise la relation fonctionnelle établie dans le paragraphe 1. et peut se démontrer par récurrence.

Propriété :

Pour tout réel a de $]0;+\infty[$ et tout entier relatif n, $ln(a^n)=nlna$ .

Démonstration :

La démonstration de cette propriété se fait par récurrence et sur le signe de n.

4. Logarithme d’une racine carrée :

Propriété :

Pour tout réel a de $]0;+\infty[$ , $ln(\sqrt{a})=\frac{1}{2}lna$ .

Preuve :

Pour a>0, $(\sqrt{a})^2=a$ donc $ln(\sqrt{a})^2=lna$

ainsi $2ln(\sqrt{a})=lna$

d’où $ln(\sqrt{a})=\frac{1}{2}lna$

Vous avez assimilé ce cours sur la fonction logarithme népérien en terminale ?

Effectuez ce QCM sur les fonctions logarithmes en classe de terminale.

Les fonctions logarithmes

Un QCM sur les fonctions logarithmes

4.2/5 - (21909 votes)

Logarithme népérien : cours de maths en terminale en PDF.

La fonction logarithme népérien : cours de maths en terminale en PDF.

I. Définition de la fonction logarithme népérien :

II. Sens de variation de la fonction logarithme népérien sur $]0;+\infty[$ :