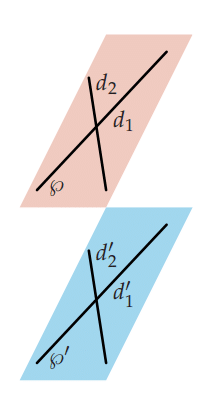🧮Cours de Mathématiques
Terminale • Lycée
Géométrie dans l’espace
📖 Temps de lecture : 5 min
🎯 Niveau : Lycée
📱 Format : Gratuit
📄 PDF : Disponible
La géométrie dans l’espace à travers un cours de maths en terminale sur l’intersection et la position relatives de droites et plans de l’espace.
Les différentes propriétés de la leçon à connaître accompagnées de figures de solides de l’espace en terminale.
Les différentes propriétés de la leçon à connaître accompagnées de figures de solides de l’espace en terminale.
I. Positions relatives de droites et plans
Propriété : positions relatives de deux droites
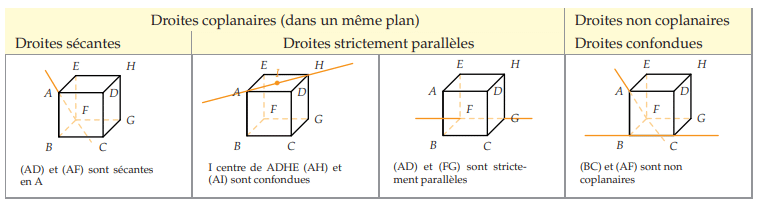
Deux droites de l’espace sont soit coplanaires (c’est-à-dire qu’il existe un plan les contenant
toutes les deux), soit non coplanaires (c’est-à-dire qu’il n’existe aucun plan les contenant
toutes les deux).
Si elles sont coplanaires, alors elles sont soit sécantes, soit parallèles (strictement parallèles
ou confondues).
toutes les deux), soit non coplanaires (c’est-à-dire qu’il n’existe aucun plan les contenant
toutes les deux).
Si elles sont coplanaires, alors elles sont soit sécantes, soit parallèles (strictement parallèles
ou confondues).
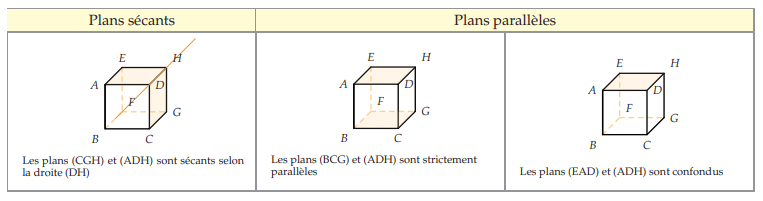
Propriété : Positions relatives de deux plans.
Deux plans de l’espace sont soit sécants (leur intersection est une droite), soit parallèles.
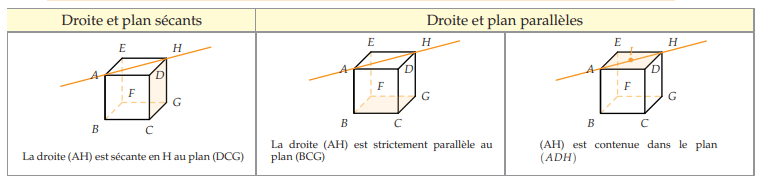
Propriété : Positions relatives d’une droite et d’un plan.
Une droite et un plan de l’espace sont soit sécants, soit parallèles.
II. Parallélisme dans l’espace
Propriété :
Si deux droites sont parallèles à une même droite alors elles sont parallèles entre elles.
Si deux plans sont parallèles à un même plan alors ils sont parallèles entre eux.
Si deux plans sont parallèles à un même plan alors ils sont parallèles entre eux.
Propriété :
Une droite est parallèle à un plan si et seulement si elle est parallèle à une droite de ce plan.
Propriété :
Si un plan P contient deux droites sécantes respectivement parallèles à deux droites sécantes
d’un plan P’ alors les plans P et P’ sont parallèles.
d’un plan P’ alors les plans P et P’ sont parallèles.
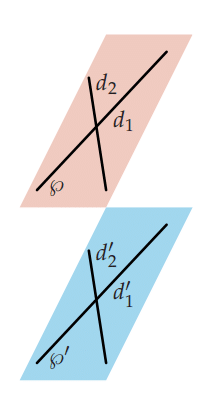
Propriété :
Si deux plans sont parallèles, alors tout plan qui coupe l’un coupe l’autre et les droites
d’intersection sont parallèles entre elles.
d’intersection sont parallèles entre elles.
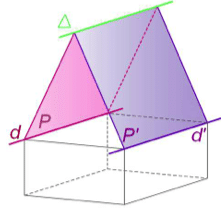
Propriété : Théorème du toit.
Soit P et P’ deux plans distincts, sécants selon une droite ∆.
Si une droite d de P est strictement parallèle à une droite d’ de P’ alors la droite ∆
intersection de P et P’ est parallèle à d et à d’.
Si une droite d de P est strictement parallèle à une droite d’ de P’ alors la droite ∆
intersection de P et P’ est parallèle à d et à d’.
