Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.

Exercice 1 :

Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur par :
a)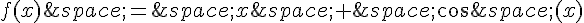
b)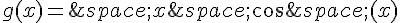

Exercice 2 :
Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur par :

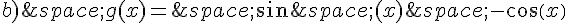
Exercice 3 :

Résoudre dans l’intervalle :
a.

b.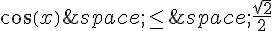 

Exercice 4 :
Résoudre dans l’intervalle :
a.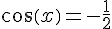

b.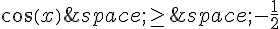

Exercice 5 :

1. Démontrer que l’équation 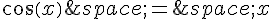admet une unique solution 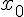dans .
2. On étudie la fonction Balayage ci-dessous, écrite en langage Python.

a) Exécuter pas à pas ce programme et compléter un tableau de suivi de la
de variable a pour p = 0,1.

Faire apparaitre également dans ce tableau.
Arrondir au centième.
Quelles sont les valeurs obtenues ?
b) Expliquer le rôle de ce programme.
c) Saisir ce programme et l’exécuter avec .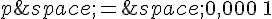

Interpréter le résultat obtenu.

Exercice 6 :

f est la fonction définie sur par :

Laquelle de ces affirmations est exacte ?
(1) La fonction f est paire.
(2) La fonction f est impaire.
(3) La fonction f n’est ni paire ni impaire.

Exercice 7 :

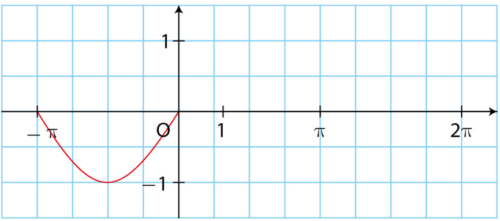
Voici la courbe représentative de la fonction sinus sur dans un repère.
Expliquer oralement comment compléter cette courbe pour l’obtenir sur .

Exercice 8 :

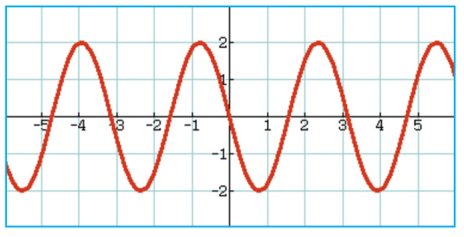
Voici la courbe représentative de la fonction g définie sur par .

1. a) Conjecturer graphiquement la parité de g.
b) Exprimer 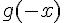en fonction de et démontrer cette conjecture.
2.Exprimer 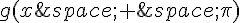en fonction de et démontrer que la fonction g est périodique de période .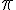

Exercice 9 :

h est la fonction définie sur par :

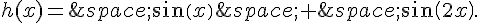
a) Démontrer que la fonction h est impaire.
b) Qu’en déduit-on pour sa courbe représentative 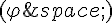dans un repère ?
c) Afficher la courbe 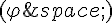à l’écran de la calculatrice et vérifier cette conjecture.

Exercice 10 :

Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur I.

Exercice 11 :

f est la fonction définie sur par :

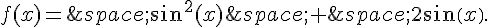
1.Montrer que pour tout x, .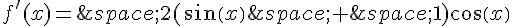

2.a) Expliquer pourquoi 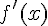est du signe de 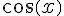sur

En déduire le signe de 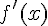sur

b) Dresser le tableau de variations de f sur

Exercice 12 :

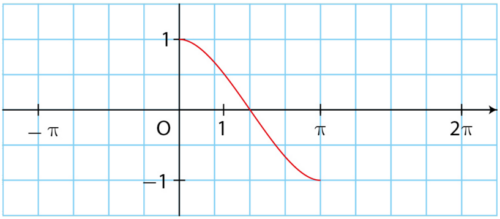
On a tracé ci-dessous la courbe représentative de la fonction cosinus sur l’intervalle
Expliquer oralement comment compléter cette courbe pour l’obtenir sur

Exercice 13 :

f est la fonction définie sur par :

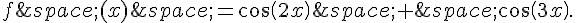
Voici ci-dessous un écran de calcul formel.

a) Vérifier les résultats.
b) Quelles propriétés de la fonction f observe-t-on ainsi ?
c) Qu’en déduit-on pour la courbe représentative de f ?

Exercice 14 :

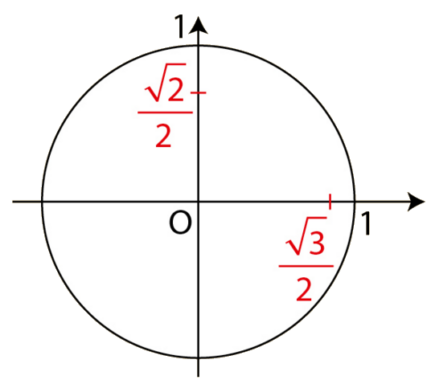
S’aider de ce cercle trigonométrique pour indiquer mentalement
les solutions dans de l’équation :

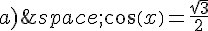
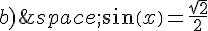
Exercice 15 :

L’Université de Manchester a mis au point une plate-forme équipée de flotteurs pour capturer l’énergie des vagues.
L’oscillation de la houle à la surface de l’eau induit l’oscillation verticale des flotteurs.

La distance d du fond marin au centre de flottaison d’un flotteur est donnée en fonction du temps t sur par :

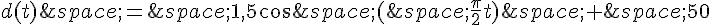
où d(t) est exprimé en mètre et t en seconde.
1. Déterminer l’amplitude du mouvement du flotteur.

2. a) Déterminer 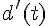sur .
b) Expliquer pourquoi 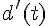est négatif sur et positif sur [2 ; 4].
c) Dresser le tableau de variations de d sur .
d) Sur quel intervalle de temps le flotteur monte-t-il ?
3. On se propose de déterminer à quel(s) instant(s) de l’intervalle , la vitesse du flotteur est maximum.
On rappelle que la vitesse à l’instant t est .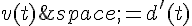
a) Déterminer la dérivée seconde 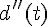sur .
b) Donner un encadrement de 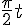pour , puis résoudre l’équation 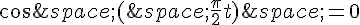 dans cet intervalle.
c) Dresser le tableau de variations de la vitesse du flotteur sur .

En déduire l’instant t de où la vitesse du flotteur est maximum.