Fonctions sinus et cosinus : cours de maths en terminale en PDF.

La fonction sinus (sin) et cosinus (cos) à travers un cours de maths en terminale. Dans cette leçon, nous aborderons la définition et la courbe de ces deux fonctions. Le tableau de variation et les propriétés algébriques et la périodicité de ces fonctions.

Vers l’an -150 avant notre ère, Hipparque de Nicée pose les principes de la trigonométrie
pour décrire avec précision la position de certains astres.
Au 2ème siècle, Ptolémée reprend ses travaux et introduit des formules de trigonométrie.
Au 5ème siècle, Aryabhata l’Ancien établit des tables du sinus.
Au 16ème siècle, Georg Joachim Rheticus définit les fonctions trigonométriques dans un triangle
rectangle au lieu d’un cercle. Il inspire François Viète qui fait évoluer la trigonométrie vers ce
qu’on en connait aujourd’hui.

Au 17ème siècle, Albert Girard introduit les notations sin et cos, reprises ensuite par Euler. René
Descartes étudie la déviation d’un rayon lumineux à l’aide du sinus.

I. Étude de la fonction sinus.

1.Propriétés de la fonction sinus.

Propriétés connues de la fonction sinus :

• La fonction sinus est impaire : pour tout réel $x\in \mathbb{R}$ , $sin(-x)=-sin(x)$
• La fonction sinus est périodique de période $2\pi$ : tout réel $x\in \mathbb{R}$ , $sin(x+2\pi)=sin(x)$ .

Propriété : continuité et dérivabilité de la fonction sinus.

• La fonction sinus est continue sur $\mathbb{R}$ .
• La fonction sinus est dérivable sur $\mathbb{R}$ . et pour tout réel x, $sin'(x) = cos(x)$ .

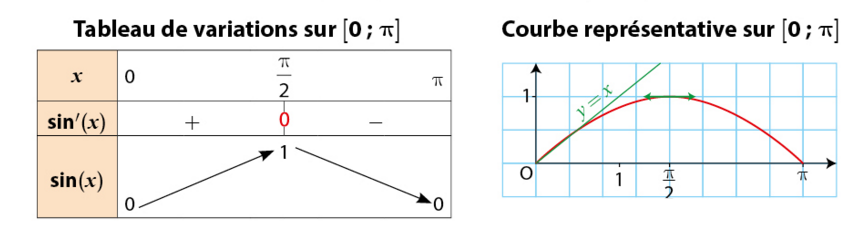
2. Étude de la fonction sinus sur l’intervalle $[0;\pi]$ .

Pour tout réel $x\in \mathbb{R}$ , $sin'(x) = cos(x)$ .
Or, $cos(x) \geq 0$ sur $[0;\frac{\pi}{2}]$ et $cos(x) \leq 0$ sur $[ \frac{\pi}{2};\pi]$ .

Donc, la fonction sinus est croissante sur $[0;\frac{\pi}{2}]$ et décroissante sur $[ \frac{\pi}{2};\pi]$ .

Dans un repère d’origine O, une équation de la tangente à la courbe représentative de la fonction sinus en l’origine O est $y = sin'(0) (x - 0) + 0$ , c’est-à-dire $y =cos(0)x$ , soit $y = x.$

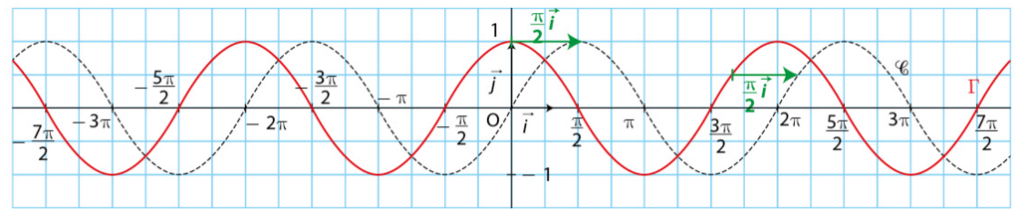
3. Courbe représentative de la fonction sinus.

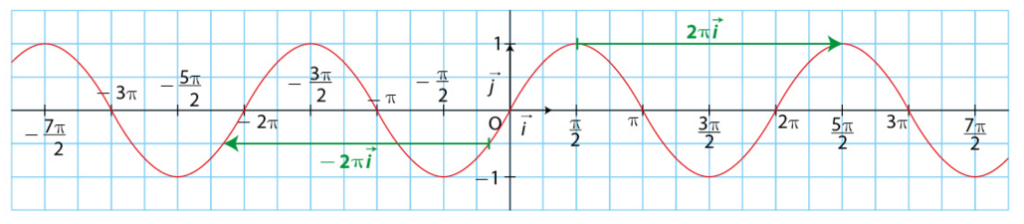
La parité de la fonction sinus permet de tracer la courbe sur l’intervalle $[-\pi;\pi]$ .
Dans un repère $(O ; \overrightarrow{i}, \overrightarrow{j })$ , d’après la périodicité de la fonction sinus, les translations de vecteurs

$-2\pi\overrightarrow{i},2\pi\overrightarrow{i},...$ permettent de tracer la courbe sur les intervalles $[- 3\pi; \pi]$ , $[\pi;3\pi]$ .

La courbe de la fonction sinus est appelée une sinusoïde.

II. Étude de la fonction cosinus.

1. Propriétés de la fonction cosinus.

Propriétés connues de la fonction cosinus :

• La fonction cosinus est paire : pour tout réel $x\in \mathbb{R}$ , $cos(-x)=cos(x)$ .
• La fonction cosinus est périodique période $2\pi$ : tout réel $x\in \mathbb{R}$ , $cos(x+2\pi)=cos(x)$ .

Propriété : continuité et dérivabilité de la fonction cosinus.

• La fonction cosinus est continue sur $\mathbb{R}$ .
• La fonction cosinus est dérivable sur $\mathbb{R}$ . et pour tout réel $x\in \mathbb{R}$ . $cos'(x)=- sin(x)$ .

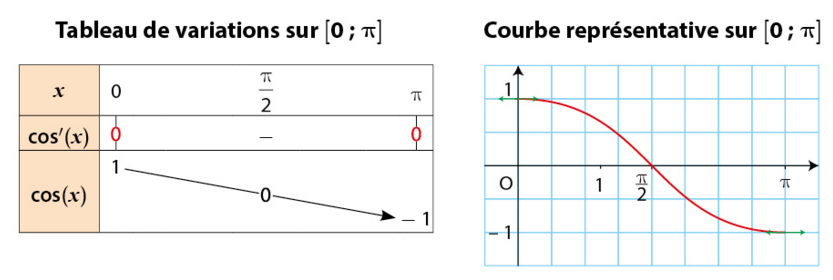
2. Étude de la fonction cosinus sur l’intervalle $[0;\pi]$ .

Pour tout réel $x\in \mathbb{R}$ , $cos'(x) = - sin(x)$ .
Or, $sin(x)\geq 0$ sur $[0;\pi]$ , donc $cos'(x) \leq 0$ sur $[0;\pi]$ .
Donc, la fonction cosinus est décroissante sur $[0;\pi]$ .

3. Courbe représentative de la fonction cosinus.

La parité de la fonction cosinus permet de tracer la courbe sur l’intervalle $[-\pi;\pi]$ .
Dans un repère $(O ; \overrightarrow{i}, \overrightarrow{j })$ , d’après la périodicité de la fonction cosinus, les translations de vecteurs $-2\pi\overrightarrow{i},2\pi\overrightarrow{i},...$ permettent de tracer la courbe sur les intervalles $[-3\pi;-\pi]$ , $[\pi;3\pi],...$

La courbe représentative $(\varphi )$ de la fonction sinus se déduit de celle $(\Gamma )$ de la fonction cosinus par la translation de vecteur $\frac{\pi}{2}\overrightarrow{i}$ .

Ainsi, la courbe $(\Gamma )$ est aussi une sinusoïde.