Fonctions polynômes du second degré : cours de maths en 2de en PDF.

1. Forme canonique

Soit a, b, c trois nombres réels avec .
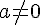On appelle fonction polynôme de degré 2 toute fonction P définie sur pouvant être exprimée sous la forme :.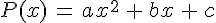
On parle aussi de fonction trinôme.

Soit P une fonction polynôme du second degré exprimée sous la forme .
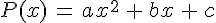Il existe deux nombres réels α et β permettant d’écrire P sous le forme :
.
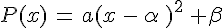Cette forme s’appelle forme canonique.

2. Étude d’une fonction trinôme

Soit a, α, β trois nombres réels et f une fonction polynôme de degré 2 définie sur par sa forme canonique .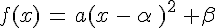
Le sens de variation d’une fonction dépend du signe de a.

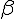Soit a, , trois nombres réels.
f une fonction polynôme de degré 2 définie sur par sa forme canonique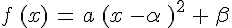
.
Sur R, la fonction f admet 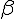comme extremum. Il est atteint pour x = α.
C’est un maximum si  est négatif.
C’est un minimum si est positif.

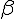Soit a, , trois nombres réels et f une fonction polynôme de degré 2 définie sur par sa
forme canonique .
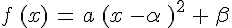Le signe d’une fonction trinôme dépend du signe de a et du signe de .
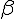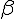
Si a < 0 et  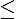0, alors la fonction est toujours négative.
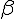
Si a > 0 et  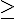0 alors la fonction est toujours positive.
Dans les autres cas,
la fonction change de signe sur l’intervalle ;
la fonction change à nouveau de signe sur l’intervalle.

Méthode : étudier une fonction trinôme du second degré.

Exemple:

On considère la fonction f définie sur par .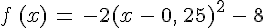
Déterminer :
1) son sens de variation ;
2) son extremum;
3) le signe de la fonction.

Correction :

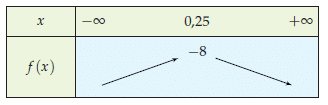
Dans le cas de la fonction f :
• α = 0, 25 • 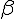= −8 • a = −2
1) a est négatif donc la fonction f est croissante sur et décroissante sinon.
2) Elle admet un maximum en x = = 0, 25. Il vaut f (0, 25) = −8.

3) La fonction f est négative sur .

3. Représentation graphique de fonctions

Soit a, α, β trois nombres réels et f une fonction trinôme définie sur par sa forme canonique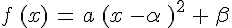
.La courbe représentative de cette fonction est une parabole qui admet un axe de symétrie : la droite d’équation x = .

Exemple :

Tracer les courbes représentatives des fonctions suivantes :
•
•
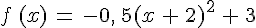
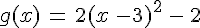
Donner leurs sens de variations et leur éventuel extremum.

Correction

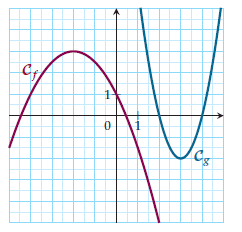
La fonction f :
• est croissante sur ]−;−2[ ;
• est décroissante sur ]−2;+[ ;
• elle admet un maximum en −2 qui vaut 3.

La fonction g :
• est décroissante sur ]−; 3[ ;
• est croissante sur ]3;+[ ;
• elle admet un minimum en 3 qui vaut −2.