Exercice 1 – Les point sont-ils alignés
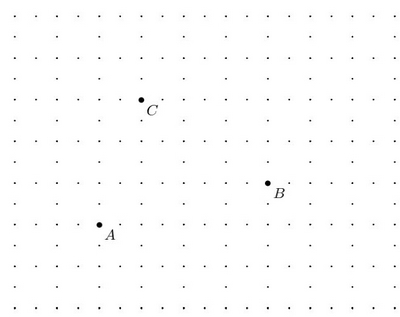
Les points P, Q et R sont-ils alignés ?
Exercice 2 – Points alignés et vecteurs
ABCD est un parallélogramme.
I est le milieu de [AB].
E est le point tel que
1. Effectuer la figure suivante.
2. Déterminer les coordonnées des points de la figure
dans le repère .
3. Les points A, E et C sont-ils alignés ?
Exercice 3 – Exprimer un vecteur en fonction de deux autres
A et B sont deux points distincts du plan .
On définit le point M par la relation vectorielle suivante :
.
1. Exprimer en fonction de
.
2. Placer le point M .
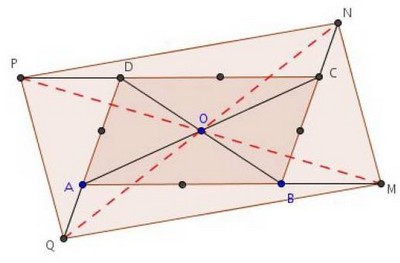
Exercice 4 – Etude d’un parallélogramme
ABCD est un parallélogramme de centre O. Les points M, N, P et Q sont tels que :
1.
a. Démontrer que .
b. Déduisez-en que O est le milieu de [MP] .
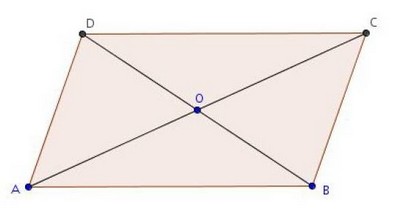
Exercice 5 – Parallélogramme
ABCD est un parallélogramme de centre O.
Donner l’ensemble des relations vectorielles possibles sur cette figure.
Exercice 6
(O,I,J) est un repère orthonormal avec OI=OJ=1 cm.
a. Placer les points A(-4;6), B(-2;-3),C(2;0),D(0;3), E(2;3).
b. Quelles sont les coordonnées des points A et B dans le repere (O;C,D)dans le repère (O;D,C)?
c. Quelles sont les coordonnées du point O dans le repère (E;C,D)?
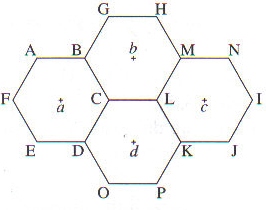
Exercice 7
La figure ci-dessous représente des hexagones réguliers de centres a,b,c,d.
1. Déterminer les images de chacun des points C,E,A,M par la translation de vecteur :
a.
b.
c.
2. Démontrer que C est le milieu de [AK].
Exercice 8
Démontrer que pour tous points A, B, C, D.
.
Exercice 9
Dans un répère, on considère les points A(-5;3), B(2;-1), C(0;4).
a. Placer les points A,B,C.
b. Calculer les coordonnées des vecteurs .
c. En déduire les coordonnées du point M tel que
d. Vérifier que B est le milieu de [AM] .
e. Calculer la distance AB .
Exercice 10
ABC est un triangle.
D,E,F sont les points tels que :
Démontrer que les points D, E, F sont alignes .
Indication : utiliser la relation de Chasles .
Exercice 11 – Droite d’EULER d’un triangle
ABC est un triangle scalène*. A’, B’, C’ sont les milieux respectifs des côtés [BC], [AC] et [AB].
O est le centre de son cercle circonscrit.
1. On note P le point défini par
a. Faire une construction à la main ou avec le logiciel de géométrie « GEOGEBRA ».
b. Montrer que:
c. Démontrer que (AP) est perpendiculaire à (BC).
d. Démontrer de même que (BP) est perpendiculaire à (AC)
e. Quelle position particulière occupe le point P ? (Dans la suite de l’exercice le point P sera noté H)
2. On note G le centre de gravité du triangle ABC, c’est à dire le point d’intersection des médianes.
On rappelle que si G est le centre de gravité du triangle ABC alors :
Montrer que :
Que déduit-on alors de la position des points O, H et G ?
Notes :
1- Scalène : un triangle est dit «scalène» lorsque ses trois côtés ont des mesures différentes.
Un triangle scalène n’est ni rectangle, ni isocèle, ni équilatéral.
2- La droite qui passe par les trois points O , H , G est appelée : « Droite d’EULER du triangle ».
Exercice 12 – Des perpendiculaires dans un triangle
On considère un triangle isocèle de base [BC] et de sommet A.
On désigne par O le centre du cercle circonscrit à ce triangle.
On désigne par M le milieu de [AB] et par G le centre de gravité du triangle AMC.
Montrer que les droites (MC) et (OG) sont perpendiculaires.
Exercice 13 – Orthogonalité dans un triangle
On considère un triangle ABC et son cercle circonscrit de centre O.
On désigne par H l’orthocentre du triangle ABC et par M le milieu de [BC].
La droite (MH) coupe, l’arc qui ne contient pas C, en I.
Montrez que les droites (MH) et (AI) sont perpendiculaires.
Exercice 14 – Déterminer les coordonnées d’un point M
Dans un repère , on donne K ( – 3 ; 5) et L(4 ; 2).
Déterminer l’abscisse du point M d’ordonnée – 2 tel que K, L et M soient alignés.
Exercice 15 – Etude de droites dans un repère
Dans un repère , on donne A(2 ;- 3) B(0 ; – 3) C( – 3 ; 0).
1. Déterminer par le calcul les coordonnées du point E tel que .
2. Que peut-on dire des droites (CE) et (AB) ? Justifier.
3. Donner les équations de (CE) et (AB).
Exercice 16 – Points alignés dans un repère
Dans un repère , on donne :
E(3 ; – 1) F(7 ; – 7) G(5 ; – 4).
Déterminer si les trois points E, F et G sont alignés.
Exercice 17 – Coordonnées et vecteurs colinéaires
1. Les vecteurs et
sont-ils colinéaires ?
2. Déterminer tel que les vecteurs
et
soient colinéaires.
Exercice 18 – Quatre points quelconques du plan
Soient A, B, C et D, quatre points quelconques du plan.
Montrer que :
Exercice 19 – Démontrer que des points sont confondus
Démontrer que les points B et D sont confondus sachant que :
Exercice 20 – Problème sur les vecteurs
A et B sont deux points distincts.
On cherche à construire le point M tel que :
1. Les vecteurs et
sont-ils colinéaires ?ont-ils le même sens?ont-ils la même norme?
2. En utilisant la relation de Chasles, montrer que l’on a l’égalité :
3. En déduire en fonction de
.
Construire le point M.
Exercice 21 – Colinéarité de deux vecteurs
Les vecteurs et
sont-ils colinéaires ?
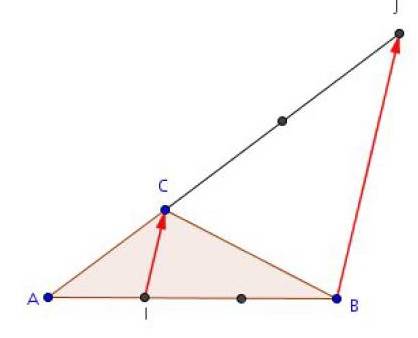
Exercice 22 – Relation de Chasles
On considère un triangle ABC et les points I et J tels que :
1. Montrer à l’aide de la relation de Chasles que .
2. Que peut-on en déduire pour les droites (BJ) et (IC) ?
Exercice 23 – Vecteurs colinéaires
Dans chacun des cas suivants, montrer que les vecteurs et
sont colinéaires.
1. .
2.
Exercice 24 – Démontrer que deux points sont confondus
Démontrer que les points A et D sont confondus sachant que :
.
Exercice 25 – Placer des points à partir d’égalités vectorielles
1. Placer le point E tel que .
2. Placer le point F tel que .
3. Placer le point G tel que .
Exercice 26
(O,I,J) est un repère orthonormal avec OI=OJ=1 cm.
a. Placer les points A(-4;6), B(-2;-3),C(2;0),D(0;3), E(2;3).
b. Quelles sont les coordonnées des points A et B dans le repère (O;C,D)dans le repère (O;D,C)?
c. Quelles sont les coordonnées du point O dans le repère (E;C,D)?
Exercice 27
Démontrer que pour tous points A, B, C, D.
.
Exercice 28
Dans un repère, on considère les points A(-5;3), B(2;-1), C(0;4).
a. Placer les points A,B,C.
b. Calculer les coordonnées des vecteurs .
c. En déduire les coordonnées du point M tel que
d. Vérifier que B est le milieu de [AM] .
e. Calculer la distance AB .
Exercice 29
ABC est un triangle.
D,E,F sont les points tels que :
Démontrer que les points D, E, F sont alignés .
Indication : utiliser la relation de Chasles .
Exercice 30 – Coordonnées de points et longueurs
Dans le plan muni d’un repère orthonormé, on note E l’ensemble des points dont les coordonnées (x;y) vérifient la relation :
.
On considère également les points F(4;0) et F'(-4;0).
1. Calculer les coordonnées des points d’intersection de E avec les axes du repères.
2. A l’aide du logiciel Geogebra, visualiser l’ensemble E et faire une conjecture sur la somme des distances MF + MF’ lorsque M est un point de E.
3. Soit M(x;y) un point de E.
a) Exprimer en fonction de
et en déduire que
.
b) Montrer que .
c) Sachant que , montrer que
puis en déduire que .
d) Valider la conjecture .
Exercice 31 – Vecteurs et parallélogramme
Soit ABCD est un parallélogramme .
1) Placer les points M et N définis par les égalités suivantes:
2) Montrer en utilisant la relation de chasles que .
3) Exprimer le vecteur en fonction des vecteurs
et
.
Exercice 32 – Coordonnées dans un repère orthonormé
Dans un repère orthonormal , on donne les points :
A(5 ; 4), B(– 1 ; 6) et C(– 3 ; 1)
1° a) Placer le point D tel que ABCD soit un parallélogramme.
Déterminer les coordonnées de D.
b) Calculer les coordonnées du point I centre du parallélogramme ABCD.
c) Le point F est le symétrique du point C par rapport au point E(– 2 ; – 1).
Calculer les coordonnées de F.
d) Calculer les coordonnées des vecteurs et
.
Que remarque-t-on ? Pouvait-on prévoir ce résultat ?
2° Soit le point M défini par : .
a) Calculer les coordonnées du point M.
b) Les points M, I et D sont-ils alignés ?
Exercice 33 – Vecteurs et parallèles
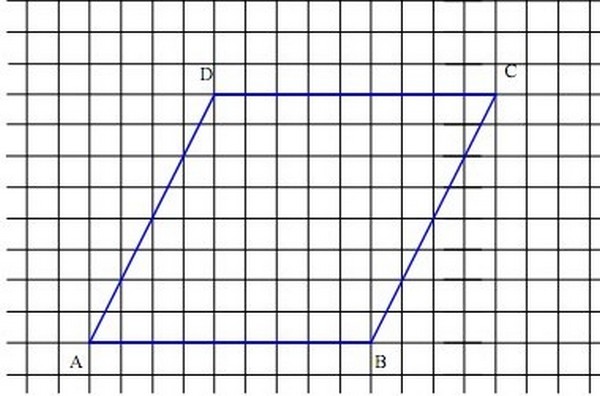
Soit ABCD un parallélogramme et soit les points M,N et P définis par :
1. Construire les points M, N et P sur la figure ci-dessous.
2. On veut démontrer que les droites (BM) et (PN) sont parallèles.
On propose deux méthode au choix :
| Méthode A :
a) Exprimer les vecteurs en fonction de b) Que peut-on dire des vecteurs c) Conclure |
Méthode B :
On se place dans le repère a) Donner (sans justification) les coordonnées des b) Calculer les coordonnées des points M, N et P. c) Conclure |






 Mathovore c'est 13 927 696 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 927 696 cours et exercices de maths téléchargés en PDF.