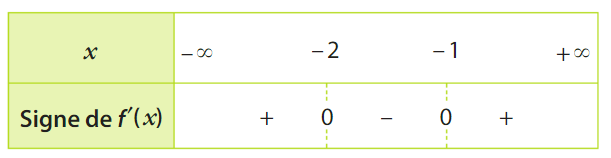Fonctions et variations : exercices de maths en 1ère corrigés en PDF.
Mis à jour le 6 août 2025
Exercice 1 – Sens de variation d’une fonction composée
Donner une décomposition de la fonction  définie par
définie par  qui permette d’en déduire son sens de variation sur l’intervalle
qui permette d’en déduire son sens de variation sur l’intervalle ![I =] - \infty ; 3]](https://mathovore.fr/latex-images/4e85e76f2cfba1fdac6ac42bd0b73512.png) .
.
Exercice 2 – Sens de variation
On considère la fonction  définie par
définie par 
1. Démontrer que 
2. En déduire que la fonction  admet un maximum en
admet un maximum en 
3. Démontrer que  .
.
4. En déduire que  est croissante sur l’intervalle
est croissante sur l’intervalle ![]-\infty;\frac{1}{2}[](https://mathovore.fr/latex-images/0a141bd6fcd3d467230eb56d6a8ce513.png) et décroissante sur
et décroissante sur ![]\frac{1}{2};+\infty[](https://mathovore.fr/latex-images/9a56ccbe1d9986e6be7ac20bbb073731.png) .
.
Exercice 3 – Comparer deux fonctions
Le but de cet exercice est de comparer les deux fonctions f et g définies sur  par :
par :

1. Calculer  .
.
2. En déduire l’intervalle sur lequel on a 
Exercice 4 – Comparaison de fonctions
Le but de cet exercice est de comparer les deux fonctions f et g définies par :
 et
et  sur l’intervalle [-1;+\infty[ » alt= »[-1;+\infty[ » align= »absmiddle » />.
sur l’intervalle [-1;+\infty[ » alt= »[-1;+\infty[ » align= »absmiddle » />.
1. Montrer que  et
et  pour tout x appartenant à
pour tout x appartenant à  .
.
2. Calculer  et
et  .
.
3. Démontrer que  pour tout x appartenant à
pour tout x appartenant à  .
.
4. En déduire une comparaison de f et g sur l’intervalle  .
.
5. Tracer sur un même repère les représentations graphiques de f et g sur l’intervalle  .
.
Exercice 5 – Fonction composée
On considère la fonction f définie par  sur
sur  .
.
Donner une formule explicite de la fonction  lorsque :
lorsque :
1.  .
.
2.  .
.
Exercice 6 – Parité
Etudier la parité de chacune des fonctions suivantes :

Exercice 7 – Etude de fonction numérique
Soit la fonction 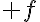 définie sur
définie sur 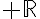 par
par 
1. Etudier les variations de 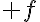 sur
sur 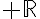 .
.
2. Déterminer les coordonnées des points d’intersection entre la courbe représentative de 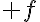 et la droite
et la droite 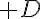 d’équation
d’équation 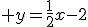 .
.
Exercice 8
Etudier les variations sur 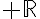 de la fonction f définie par
de la fonction f définie par 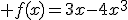 .
.
Exercice 9
Soit f la fonction définie sur 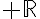 par :
par :
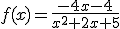 .
.
1. Etudier les variations de f sur 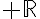 .
.
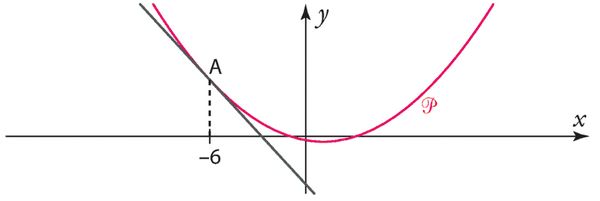
2. Déterminer les coordonnées du point A, intersection entre la courbe représentative de f et l’axe des abscisses .
3. Déterminer une équation de la tangente T à la courbe représentative de 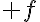 au point A.
au point A.
Exercice 10
Etudier les variations sur ]-2 ; 1[ de la fonction 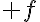 définie par :
définie par :
 .
.
Exercice 11 – Forme canonique et factorisée
Déterminer la forme canonique et factorisée de :

Exercice 12 – Etude de fonctions du second degré
On note  et
et 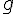 deux fonctions polynômes du second degré, définies par :
deux fonctions polynômes du second degré, définies par :
 et
et 
On note  et
et 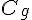 leur représentation graphique respectives dans un repère orthogonal
leur représentation graphique respectives dans un repère orthogonal 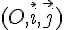 .
.
1. Déterminer le domaine de définition de  puis celui de
puis celui de 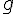 .
.
2. Déterminer la forme canonique puis factorisée de 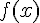 .
.
3. Déterminer la forme développée puis canonique de  .
.
4. Déterminer les coordonées des points d’intersection entre  et les axes du repère.
et les axes du repère.
5. Déterminer les coordonées des points d’intersection entre 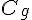 et les axes du repère.
et les axes du repère.
6. Dresser le tableau de variation de  puis celui de
puis celui de 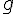 .
.
7. Décrire  puis
puis 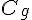 .
.
8. Déterminer les coordonnées des points d’intersection entre  et
et 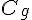 .
.
9. Etudier la position relative entre les deux courbes  et
et 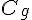 .
.
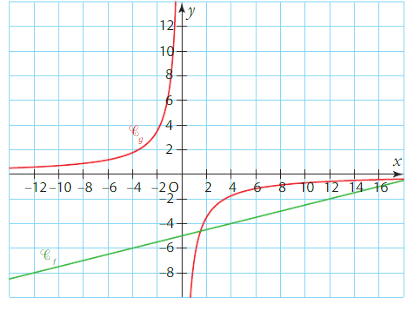
Exercice 13 – Etude d’une fonction inverse et de l’hyperbole
f est la fonction  définie sur
définie sur 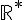 .
.
g est la fonction  définie sur
définie sur  .
.
Dans un repère orthonormal  , C et D sont les courbes représentant f et g.
, C et D sont les courbes représentant f et g.
1. Tracer les courbes C et D.
2. Démontrer que le point d’abscisse 1 de D appartient à C.
Trouver le second point d’intersection de ces courbes.
indication : Vérifier que x² – 3x + 2 = (x – 1)(x – 2)
3. Vérifier les coordonnées de ces points d’intersection sur le graphique.
4. Construire l’ensemble des points M(x; y) tels que x² y² = 4.
5. Un rectangle a pour aire 2 m² et pour périmètre 6m.
En utilisant le graphique précédent, trouver sa longueur et sa largeur.
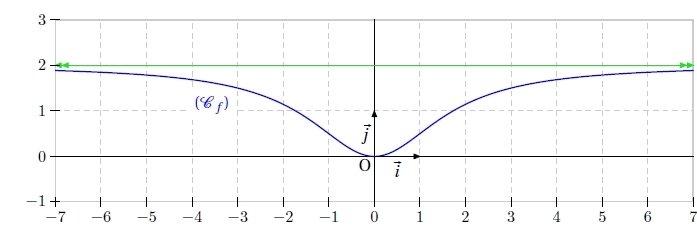
Exercice 14 – Etude d’une fonction
On considère la fonction f définie par :

1. Déterminer son ensemble de définition.
2. Démontrer que f est une fonction positive sur  .
.
3. Etudier la parité de la fonction f.
4. Tracer soigneusement la représentation graphique Cf de la fonction f.
On se limitera à l’intervalle [- 3 ; 3 ].
5. Donner, par lecture graphique, la valeur du maximum de la fonction f sur :
a. l’intervalle [-1;1].
b. l’intervalle [-2;1].
6. Résoudre l’inéquation  .
.
Exercice 15 – Comparaison de fonctions
Le but de cet exercice est de comparer les fonctions f et g définies par :
 et
et  sur l’intervalle
sur l’intervalle  .
.
1. Montrer que  et
et  pour tout
pour tout  .
.
2. Calculer  et
et  .
.
3. démontrer que  pour tout
pour tout  .
.
4. En déduire une comparaison de f et g sur l’intervalle  .
.
5. Tracer sur un même repère les représentation graphique de f et g sur l’intervalle  .
.
Exercice 16 – Parité
Etudier la parité des fonctions suivantes :
 sur
sur 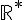
 sur
sur 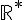
Exercice 17 – Composée
On considère la fonction f définie par  sur
sur  .
.
Donner une formule explicite de la fonction  lorsque :
lorsque :
 sur
sur ![]-\infty;1]](https://mathovore.fr/latex-images/d3953e92730270bb41c785bbc30be86e.png) puis
puis  sur
sur 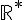 .
.
Exercice 18 – Composée de fonctions de référence
Soit la fonction  définie par
définie par  sur
sur 
En considérant la fonction f comme la composée de fonctions de référence, préciser le sens de variations de f sur l’intervalle I.
Exercice 19 – Sens de variation d’une fonction composée
On donne  et
et 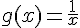 .
.
On définit la fonction  définie sur
définie sur ![I=]-\infty;\frac{1}{3}[](https://mathovore.fr/latex-images/7d5363ea561e64340282ded7b2b779b6.png) par
par  .
.
1. Donner l’expression de  .
.
2. Déterminer le sens de variation de  sur I .
sur I .
Exercice 20 – Ensemble de définition d’une fonction composée
On considère les fonctions f et g définies par :
 .
.
1. Calculer  .
.
2. Quel est l’ensemble de définition de  ?
?
Exercice 21 – Fonction majorée
Soit la fonction définie par
définie par  .
.
1. Déterminer les réels a et b tels que  .
.
2. Montrer que f est majorée par 2.
Exercice 22 – Forme canonique
On considère la fonction  définie sur
définie sur  par :
par :

1. Déterminer la forme canonique de  .
.
2. Décrire la courbe de  .
.
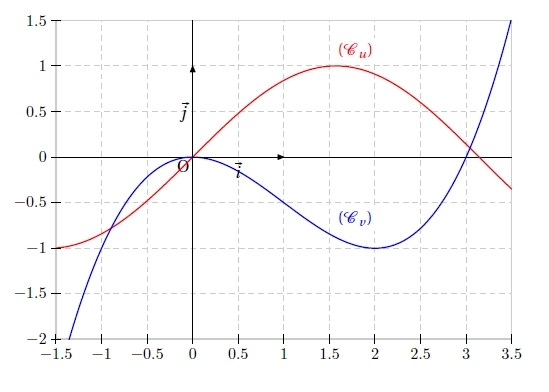
Exercice 23 – Tracer la courbe de la somme de deux fonctions
u et v sont représentées ci-dessous.
Tracer sur ce graphique la courbe représentative de la fonction u + v.
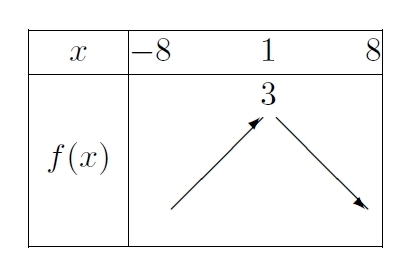
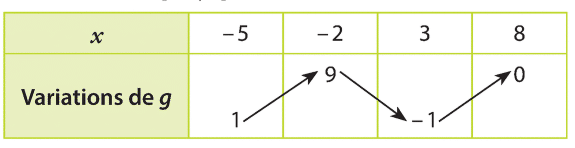
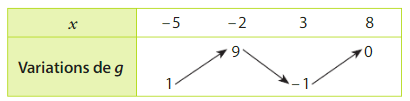
Exercice 24 – Exploitation d’un tableau de variation
Voici le tableau de variations d’une fonction  définie sur
définie sur  :
:
On donne f( – 2) = – 1 et f(2) = 0.
On définit les fonctions suivantes :

1. Donner les valeurs de g (1), h (2), p (1) et r ( – 1).
2. Etablir les tableaux de variations de h, r, p et g.
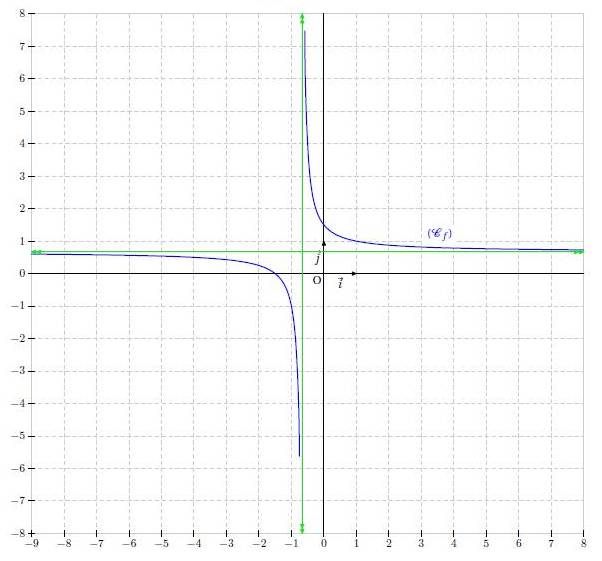
Exercice 25 – Fonction rationnelle
Soit la fonction  définie par :
définie par :

1. Etudier les limites de f. Interpréter graphiquement.
2. Etudier les variations de f. Donner le tableau de variations complet.
Exercice 26 – Fonctions composées commutatives
Soient  et
et 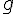 les fonctions définies sur
les fonctions définies sur  par :
par :
 et
et 
Démontrer que 
Exercice 27 – Comparaison de racines
Soient 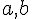 dans
dans  .
.
1. Développer 
2. Démontrer que 
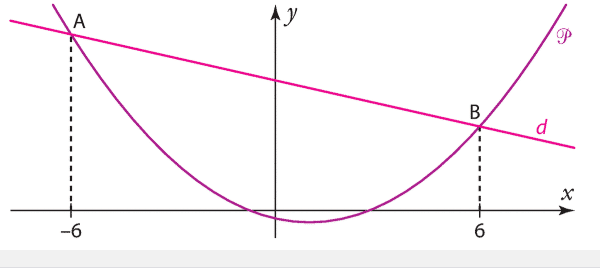
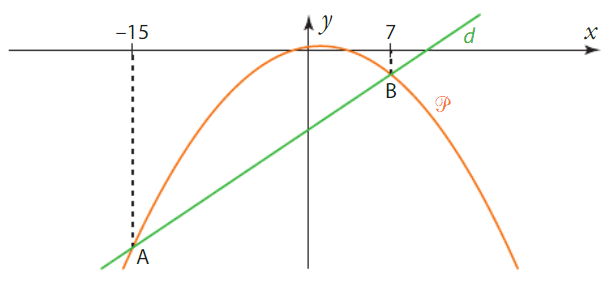
Exercice 28 :
1)Recopier et compléter les phrases suivantes.
a) » La parabole 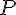 et la droite d se coupent en … ».
et la droite d se coupent en … ».
b) » La parabole 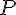 est située strictement au-dessus de la droite d sur … ».
est située strictement au-dessus de la droite d sur … ».
« La parabole 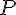 est située strictement en-dessous de la droite d sur … ».
est située strictement en-dessous de la droite d sur … ».
2)En déduire les solutions des équations et inéquations.
a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).
Exercice 29 :
1)Etudier la position relative de la parabole 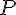 et de la droite
et de la droite 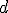 .
.
2)En déduire les solutions des équations et des inéquations suivantes :
a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).
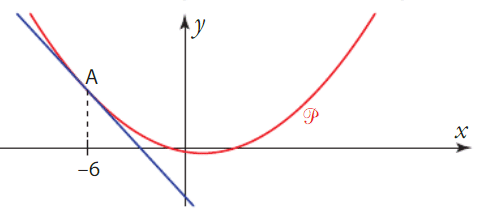
Exercice 30 :
Soient f et g deux fonctions définies sur  dont les courbes
dont les courbes  et
et 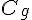 sont représentées
sont représentées
ci-dessous dans un repère du plan.
1)Etudier la position relative des courbes  et
et 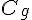 .
.
2) En déduire les solutions des équations et inéquations suivantes.
a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).
Exercice 31 :
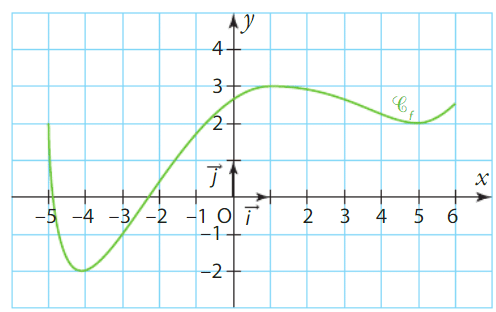
Soit f une fonction définie et dérivable sur l’intervalle [- 5 ; 6 ].
La courbe représentative de f est tracée ci-dessous dans un repère du plan.
1)Décrire les variations de f sur [- 5 ; 6].
2) En déduire le tableau de signes de la fonction dérivée f ‘ sur [- 5 ; 6 ].
Exercice 32 :
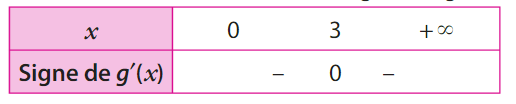
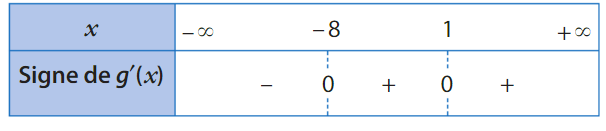
Soit g une fonction dérivable sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et g ‘ sa dérivée.
et g ‘ sa dérivée.
On donne le tableau de signes de g ‘.
La fonction g admet-elle un extremum local ?
Si oui, est-ce un maximum ?
Exercice 33 :
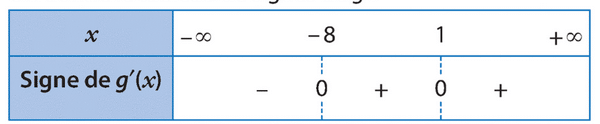
Soit g une fonction dérivable sur  et g ‘ sa dérivée.
et g ‘ sa dérivée.
On donne le tableau de signes de g ‘.
1)La fonction g admet-elle un minimum local ?
Si oui, en quelle valeur ?
2)La fonction g admet-elle un maximum local ?
Si oui, en quelle valeur?
Exercice 34 :
Soit f la fonction définie sur  par
par  .
.
1)Justifier que f est dérivable sur  et calculer f ‘ (x) pour tout réel x.
et calculer f ‘ (x) pour tout réel x.
2)Dresser le tableau de signes de f ‘ (x) sur  .
.
3)En déduire que f admet un extremum local en une valeur que l’on déterminera.
Exercice 35 :
On a le tableau de variations d’une fonction g définie et dérivable sur [- 5 ; 8 ].
a)Donner un encadrement de g(x) lorsque  .
.
b)Donner un encadrement de g(x) lorsque  .
.
c)Donner un encadrement de g(x) lorsque  .
.
d) Soient a et b deux réels tels que  .
.
e) Soient a et b deux réels tels que  .
.
Comparer g(a) et g(b).
f) Soit ![a\in[-5;-2]](https://mathovore.fr/latex-images/dc21f2e2ee913282680d9358e86e1314.png) et
et ![b\in[3;8]](https://mathovore.fr/latex-images/9196cfc30574a39f79f96f9ce1cf3e0f.png) . Comparer g(a) et g(b).
. Comparer g(a) et g(b).
Exercice 36 :
1. Etudier la position relative de la parabole 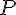 et de la droite d.
et de la droite d.
2. En déduire les solutions des équations et inéquations.
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x) < g(x)
Exercice 37 :
1.Étudier la position relative de la parabole 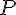 et de la droite d.
et de la droite d.
2.En déduire les solutions des équations et inéquations suivantes :
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x) < g(x)
Exercice 38 :
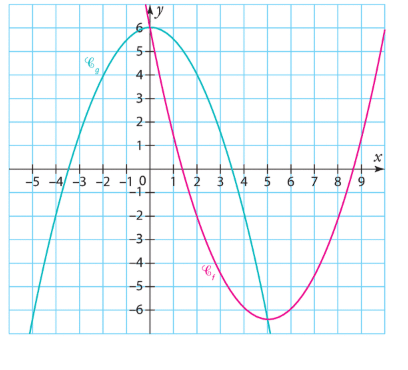
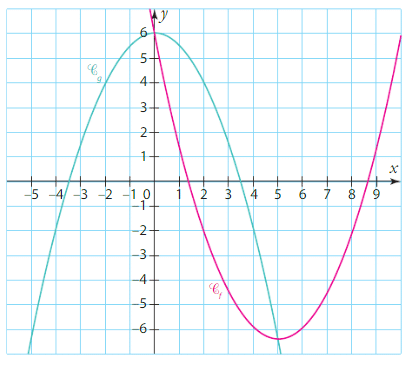
Soient f et g deux fonctions définies sur  dont les courbes
dont les courbes  et
et 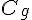 sont représentées ci-dessous dans un repère du plan.
sont représentées ci-dessous dans un repère du plan.
1 . Étudier la position relative des courbes  et
et 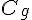 .
.
2. En déduire les solutions des équations et inéquations suivantes.
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x)< g(x)
Exercice 39 :
Soit f et g deux fonctions définies sur  par
par  et
et  .
.
1. Montrer, que pour tout réel x,  .
.
2. Étudier, selon les valeurs de x, le signe de f(x) — g(x).
3. En déduire la position relative des courbes  et
et 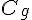 .
.
Exercice 40 :
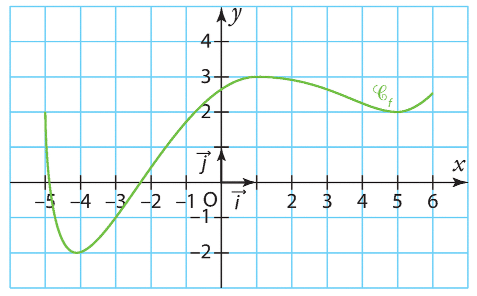
Soit f une fonction définie et dérivable sur l’intervalle [- 5 ; 6].
La courbe représentative de f est tracée ci-dessous dans un repère du plan.
1.Décrire les variations de f sur [- 5 ; 6].
2.En déduire le tableau de signes de la fonction dérivée  sur [-5 ; 6].
sur [-5 ; 6].
Exercice 41 :
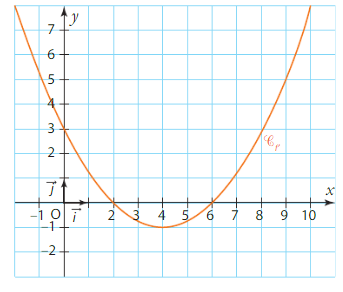
Soit f une fonction définie et dérivable sur l’intervalle [- 2 ; 10].
Sa dérivée est la fonction  représentée par la courbe ci-dessous dans un repère du plan.
représentée par la courbe ci-dessous dans un repère du plan.
1 . Lire graphiquement le signe de  selon les valeurs de x de l’intervalle [ – 2 ; 10].
selon les valeurs de x de l’intervalle [ – 2 ; 10].
Et présenter vos résultats dans un tableau de signes.
2. En déduire le tableau de variations de la fonction f sur l’intervalle [ – 2 ; 10].
Exercice 42 :
Soit f une fonction dérivable sur  et
et  sa dérivée. On donne le tableau de signes de
sa dérivée. On donne le tableau de signes de  .
.
La fonction f admet-elle un extremum local ? Si oui, est-ce un maximum ou un minimum ?
Exercice 43 :
Soit g une fonction dérivable sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et
et 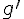 sa dérivée.
sa dérivée.
On donne le tableau de signes de 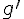 .
.
La fonction g admet-elle un extremum local ? Si oui, est-ce un maximum ou un minimum ?
Exercice 44 :
Soit f une fonction dérivable sur  et
et  sa dérivée.
sa dérivée.
On donne le tableau de signes de  .
.
1. La fonction f admet-elle un minimum local ? Si oui, en quelle valeur ?
2. La fonction f admet-elle un maximum local ? Si oui, en quelle valeur ?
Exercice 45 :
Soit g une fonction dérivable sur  et
et 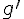 sa dérivée.
sa dérivée.
On donne le tableau de signes de 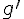 .
.
1. La fonction g admet-elle un minimum local ? Si oui, en quelle valeur ?
La fonction g admet-elle un maximum local ? Si oui, en quelle valeur ?
Exercice 46 :
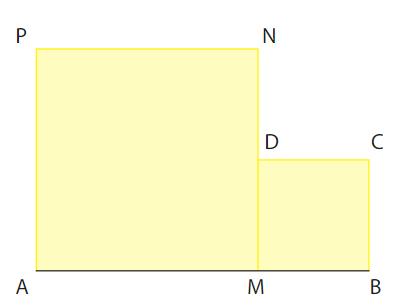
Soit un segment [AB] de longueur 10 et M un point de ce segment.
Du même côté de ce segment, on construit deux carrés AMNP et MBCD.
On pose AM = x et on étudie l’aire du domaine formé par ces deux carrés en fonction de x.
1.A quel intervalle I appartient le réel x ?
2. Soit f(x) l’aire du domaine.
Montrer que, pour tout réel x de l, on a:

3. Justifier que la fonction f est dérivable sur I et déterminer 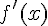 pour tout x de I.
pour tout x de I.
4. En déduire les variations de f sur I et la valeur de x pour laquelle l’aire du domaine est minimale.
Exercice 47 :
Soit f une fonction définie sur  par
par  et g une fonction définie sur
et g une fonction définie sur 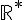 par
par  .
.
a) Montrer que, pour tout réel x non nul :
 .
.
b) Étudier, selon les valeurs de x, le signe de f(x) — g(x).
c) En déduire la position relative des courbes  et
et 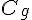 .
.
Exercice 48 :
On a le tableau de variations d’une fonction g définie et dérivable sur [ – 5 ; 8] :
a) Donner un encadrement de  lorsque
lorsque  .
.
b) Donner un encadrement de  lorsque
lorsque  .
.
c) Donner un encadrement de  lorsque
lorsque  .
.
d) Soient a et b deux réels tels que 
Comparer g(a) et g(b).
e) Soient a et b deux réels tels que 
Comparer g(a) et g(b).
f) Soit ![a\,\in\,[-5\,;-2]](https://mathovore.fr/latex-images/67cc23f883428d6760ff3f034698d93c.png) et
et ![b\,\in\,[3\,;8]](https://mathovore.fr/latex-images/66362e9e72a9f84f5b16440a96f4714d.png) .
.
Comparer g(a) et g(b).
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions et variations : exercices de maths en 1ère corrigés en PDF.» au format PDF.
Ressources de première
Cours de première
Exercices de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.