Limite de fonctions : exercices de maths en terminale corrigés en PDF.

Mis à jour le 28 juillet 2025

✏️Exercices

Terminale • Lycée

Limite de fonctions

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les limites et asymptotes à travers des exercices de maths en terminale corrigés. Consultez également les exercices de corrigés en terminale en PDF .

Exercice 1 – Limite de fonctions

Voici quelques limites à calculer. Ce sont toutes des formes indéterminées et on se limitera aux fonctions polynômes, rationnelles (quotient de deux polynômes) ou comportant des racines carrées.

$\lim_{x\to\,+\infty}\frac{x^2+x-1}{x-1}$
$\lim_{x\to\,+\infty}\frac{x+100}{x^2+x}$
$\lim_{x\to\,+\infty}\frac{x^3}{x^2+x+1}-x$
$\lim_{x\to\,+\infty}\frac{x^3}{2x^2-1}-\frac{x^2}{x+1}$
$\lim_{x\to\,+\infty}\frac{3x^2}{2x+1}-\frac{(2x-1)(3x^2+x+2)}{4x^2}$
$\lim_{x\to\,+\infty}\frac{\sqrt{x+5}}{x-4}$
$\lim_{x\to\,+\infty},\sqrt{x^2+x-1},-2x$
$\lim_{x\to\,+\infty},\sqrt{x^2+x-1},-x$
$\lim_{x\to\,+\infty},\sqrt{x^2+2x},-\sqrt{x^2+3}$

Exercice 2 – Une limite classique

On rappelle que $\lim_{t\to\,0}\frac{sin(t)}{t}=1$ .Soit n entier naturel.

Etudier la limite suivante : $\lim_{t\to\,0}\frac{sin(nt)}{t}$ .

Exercice 3 :

f est la fonction définie sur l’intervalle $[0\,;\,+\infty[$ par $f(x)=\sqrt{x}$ .
a) Démontrer que pour tout réel $A\,\geq\,\,0$ , l’intervalle $]A\,;\,+\infty[$ contient toutes les valeurs f(x) pour x assez
grand.
b) Que peut-on en déduire pour la fonction f ?

Exercice 4 :

$g$ est la fonction définie sur $]0\,;\,+\infty[$ par $g(x)\,=\frac{1}{x^2}$ .
a) Démontrer que pour tout réel $\alpha\,>0$ , l’intervalle $]0\,;\,\alpha\,[$ ; contient toutes les valeurs g(x) pour x assez grand.
b) En déduire la limite de la fonction g en $+\infty$ .
c) Interpréter graphiquement cette limite pour la courbe représentative $(\varphi\,)$ de g dans un repère orthonormé.

Exercice 5 :

f est la fonction définie sur $[0\,;\,+\infty[$ par :
$f(x)=\sqrt{x}+2$ .
a) Démontrer que f(x) > 100 pour x assez grand.
b) Démontrer que pour tout réel A > 2, l’intervalle $]A\,;\,+\infty[$ contient toutes les valeurs f (x) pour x assez
grand.
c) Que peut-on en déduire pour la fonction f ?

Exercice 6 :

g est la fonction définie sur $]0\,;\,+\infty[$ par :
$g(x)\,=\frac{1}{x}\,+\,1$ .
a) Démontrer que pour tout réel $\alpha\,>\,1$ , l’intervalle $]1;\alpha\,[$ contient toutes les valeurs g(x) pour x assez grand.
b) En déduire la limite de la fonction g en $+\infty$ .
c) Interpréter graphiquement cette limite pour la courbe $(\varphi\,)$ de g dans un repère orthonormé.

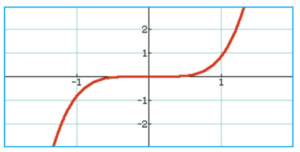
Exercice 7 :

h est la fonction définie sur $\mathbb{R}$ par :
$h(x)=\,2sin\,(x)\,-x^2$ .
a) Utiliser la courbe de h affichée ci-dessous pour conjecturer les limites de h en $+\infty$ et en $-\infty$ .
b) Démontrer ces conjectures.

Exercice 8 :

f est la fonction définie sur $\mathbb{R}$ par $f(x)\,=\,x^3\,-\,5x+\,2$ .
a) Vérifier que l’étude de la limite de la fonction f en $+\infty$ , avec les règles opératoires, mène à une forme
indéterminée.
b) Étudier la limite de la fonction f en $+\infty$ .

Exercice 9 :

g est la fonction définie sur $]3;\,+\infty[$ par $g(x)=\frac{2x+1}{x-3}$ .
Étudier la limite de la fonction g: a) en $+\infty$ ; b) en 3.

Exercice 10 :

f est la fonction définie sur $\mathbb{R}$ par :

$f(x)=-x^4+3x+1$ .
a) Vérifier que l’étude de la limite de la fonction f en $+\infty$ , avec les règles opératoires, mène à une forme
indéterminée.
b) Étudier la limite de la fonction f en $+\infty$ .

Exercice 11 :

f est la fonction définie sur $]-1;\,+\infty[$ par :

$f(x)=\frac{4x+5}{x+1}$
Étudier la limite de la fonction f:
a. en $+\infty$ . b. en $-1$ .

Exercice 12 :

Soit $f\,:\,x\,\mapsto \,-(x-\,3)^2$ , définie pour tout réel x et $g\,:\,x\,\mapsto \,-2+\frac{1}{2x}$ définie pour tout réel $x\neq\,0$ .
1. Tracer les courbes représentatives des fonction f et g entre les abscisses 0 et 10.
2. Relever graphiquement à partir de quelle valeur de x on a :
$a)f(x)<-10$ $b)g(x)\in\,]-2;0[$
3. Conjecturer les limites de f et g en $+\infty$ et en $-\infty$ .

Exercice 13 :

Déterminer les limites suivantes :

$a)\lim_{x\to\,+\infty}e^x+2sin(x)\\b)\lim_{x\to\,-\infty}e^xcos(x)\\c)\lim_{x\to\,+\infty}\frac{1+3cos(x)}{(x+1)^2}\,\\d)\lim_{x\to\,-\infty}\frac{sin(x)}{x}$

Exercice 14 :

Déterminer les limites suivantes :

$a)\,\lim_{x\to\,-\infty}\sqrt{2-x}\\b)\,\lim_{x\to\,-1^+}e^{\sqrt{x+1}}$

Exercice 15 :

Déterminer les limites suivantes :

$a)\lim_{x\to\,-\infty}\sqrt{1+e^x}\\\\b)\lim_{x\to\,1^+}e^{\frac{1}{x-1}}$

Exercice 16 :

g est la fonction définie sur l’intervalle $]0;+\infty[$ par $g(x)=\frac{1}{x}+1$ .

Démontrer que, pour tout nombre réel $\alpha\,>0$ , l’intervalle $]1-\alpha\,;1+\alpha\,[$ contient toutes les valeurs g(x) pour x assez grand.
En déduire la limite de la fonction g en $+\infty$ .
Interpréter graphiquement cette limite.

Exercice 17 :

h est la fonction définie sur l’intervalle $]1;+\infty[$ par $h(x)=\frac{1}{x^2-1}$ .

1.Démontrer que, pour tout nombre réel $\alpha\,>0$ , l’intervalle $]-\alpha\,;+\alpha\,[$ contient toutes les valeurs

h(x) pour x assez grand.

2.En déduire la limite de la fonction h en $+\infty$ .

3.Interpréter graphiquement cette limite.

Exercice 18 :

f est la fonction définie sur $\mathbb{R}$ par $f(x)=-x^2+3x+1$ .

Etudier la limite de f en $+\infty$ .

2. g est une fonction définie sur l’intervalle $]-1;+\infty[$ par $g(x)=\frac{4x^2-x+5}{x+1}$ .

Etudier la limite de la fonction g.

a) en $+\infty$ b) en – 1.

Exercice 19 :

g est la fonction définie sur $\mathbb{R}$ par $g(x)=\frac{e^x+1}{e^x-1}$

Etudier la limite de la fonction g en $-\infty$ .
a) Démontrer que, pour tout nombre réel x, $g(x)=\frac{1-e^{-x}}{1+e^{-x}}$ .

b) Etudier la limite de la fonction g en $+\infty$ .

Exercice 20 :

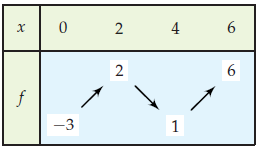
Dans chacun des cas, on donne le tableau de variation d’une fonction f.

Tracer, à main levée, une courbe $\varphi$ susceptible de représenter la fonction f dans un repère.

Exercice 21 :

Donner, sans justification, la limite des fonctions suivantes en $+\infty$ .

$a)\,f(x)=x\sqrt{x}\\b)\,g(x)=(x^2+1)(-x^2+2)\\c)\,h(x)=e^x\,(\,\frac{1}{x}\,+2\,)\\d)\,k(x)=x^2\,(\,-3-\,\frac{1}{x}\,\,)$

Exercice 22 :

Une usine fabrique une puce destinée aux appareils électroniques.

Le coût total de fabrication est modélisé par la fonction C définie sur l’intervalle $[0;+\infty[$

par $C(q)=\frac{8}{1+e^{-q}}$ où q désigne la quantité de puces fabriquées (en milliers)

et C(q) le coût total (en millions d’euros).

a. Représenter graphiquement la fonction C à l’écran de votre calculatrice.

b. Etudier la limite de la fonction C en $+\infty$ .

2. On note $C_M(q)$ le coût moyen de fabrication d’une puce lorsqu’on en fabrique q (avec q>0).

a. Exprimer $C_M(q)$ en fonction de q.

b. Représenter graphiquement la fonction $C_M$ à l’écran de la calculatrice.

c. Etudier la limite de la fonction $C_M$ en $+\infty$ .

Interpréter le résultat obtenu en termes économiques.

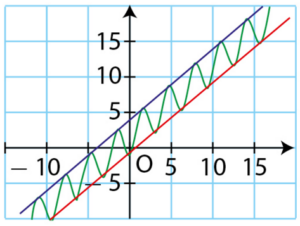
Exercice 23 :

g est la fonction définie sur $\mathbb{R}$ par :
$g(x)=\,x^4sin(x)$ .
Louise a affiché la courbe représentative de g à l’écran de sa calculatrice.
Elle conjecture : « La fonction g a pour limite $+\infty$ en $+\infty$ . »
a) k désigne un nombre entier naturel.
Calculer $g(k\pi)$ .
b) Expliquer alors pourquoi Louise se trompe.

Exercice 24 :

Voici dans un repère orthonormé la courbe représentative de la fonction f:
$x\,\mapsto \,x-1\,+5\,sin^2\,(x)$
et les droites d’équations
y = x— 1 et y=x+ 4.
Étudier les limites de la fonction f en $-\infty$ et en $+\infty$ .

Exercice 25 :

Voici la courbe représentative $\varphi$ d’une fonction f définie sur $]-\,\infty,\,-2[\,\cup\,]-\,2;\,+\,\infty,[$ .
1. Lire sur le graphique, les limites de la fonction f en $-\infty$ , en $+\infty$ , à droite et à gauche en – 2.
2. g est la fonction définie pour x différent de – 2 et de 0 par $g(x)\,=\,\frac{1}{f(x)}$ .
Déterminer Ia limite de la fonction g en :
a) $-\infty$ b) $+\infty$ c) $-2$ d) à droite et à gauche en O.
3. h est la fonction définie sur $]-\,\infty,\,-2[\,\cup\,]0;\,+\,\infty,[$ par $h(x)=\sqrt{f(x)}$ .

Déterminer la limite de la fonction h en :
a) $-\infty$ b) $+\infty$ c) $-2$ d) O.

Exercice 26 :

g est la fonction définie sur $[0\,;\,+\infty[$ par :
$g(x)=\frac{2x-1}{\sqrt{x^2+1}}$
a) Montrer que pour tout x > 0,
$g(x)=\frac{2-\frac{1}{x}}{\sqrt{1+\frac{1}{x^2}}}$
b) Déterminer l’équation de l’asymptote à la courbe représentative de g dans un repère orthonormé.

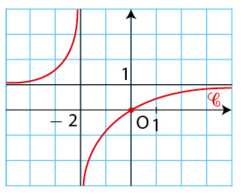
Exercice 27 :

g est la fonction définie sur $\mathbb{R}$ par :
$g\,(x)\,=\,e^{-x}\,sin(x).$
On note $\varphi$ la courbe représentative de la fonction g dans un repère orthonormé.
a) Utiliser un encadrement de g(x) pour étudier la limite de g en $+\infty$ .
b) En déduire une asymptote d à la courbe $\varphi$ .
c) Montrer que la courbe $\varphi$ coupe une infinité de fois son asymptote d.
2. Numa affirme : « La limite de la fonction g en $-\infty$ est $+\infty$ ».

Expliquer pourquoi Numa se trompe.

Exercice 28 :

1. h est la fonction définie $[0\,;\,+\infty[$ par :
$h(x)=\frac{e^{2x}}{x+e^x}$
Voici la courbe représentative de la fonction h à l’écran d’une calculatrice.

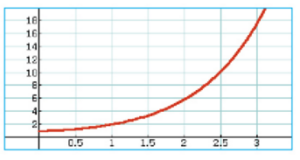
a) Conjecturer la limite de la fonction h en $+\infty$ .
b) Démontrer cette conjecture.
Conseil : mettre $e^x$ en facteur au dénominateur.
2. k est la fonction définie sur $]-\infty\,;\,-1]$ par $k(x)=\frac{e^{2x}}{x+e^x}$
a) Afficher la courbe représentative de k à l’écran de la calculatrice et conjecturer la limite de k en $-\infty$ .
b) Prouver cette conjecture.

Exercice 29 :

Pour tout réel a, on note $h_a$ la fonction définie sur $\mathbb{R}$ par $h_a(x)=\frac{ax+\frac{1}{2}}{e^x}$
1 . a) Déterminer la limite de la fonction $h_a$ en $+\infty$ .
b) Suivant les valeurs du nombre réel a, déterminer la limite de la fonction $h_a$ en $-\infty$ .
2. a) Démontrer que pour tout réel x :
$h_a'(x)=\frac{-ax+a-\frac{1}{2}}{e^x}$
b) Démontrer que pour tout réel $a\neq\,0$ , la fonction $h_a$ admet un extremum pour une valeur de x que l’on exprimera en fonction de $a$ .
3. Dans un repère orthonormé, on note $\varphi\,_a$ la courbe représentative de la fonction $h_a$ .
Voici les courbes pour cinq valeurs de a :

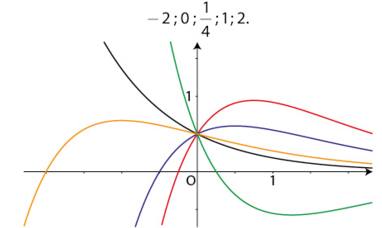
Déterminer, pour chacune des courbes tracées, la valeur de a correspondante, en justifiant les réponses.

Exercice 30 :

Pour tout réel non nul $\lambda$ , on désigne par $f_\lambda$ la fonction définie sur R par :
$f_\lambda(x)=\frac{e^{\lambda\,x}+e^{-\lambda\,x}}{2\lambda}$

1.a) Tracer, à l’aide d’un logiciel de géométrie, la courbe représentative de la fonction $f_\lambda$ .

b) Conjecturer, suivant les valeurs de $\lambda$ , les limites de la fonction $f_\lambda$ en $-\infty$ et en $+\infty$ .
2. Démontrer les conjectures précédentes.

4.3/5 - (26669 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «limite de fonctions : exercices de maths en terminale corrigés en PDF.» au format PDF.

Ressources de terminale

D'autres cours et exercices à consulter

La récurrence : exercices de maths en terminale corrigés en PDF.

Suites numériques : exercices de maths en terminale corrigés en PDF.

Intégrales et primitives : exercices de maths en terminale corrigés en PDF.

Les équations différentielles : exercices de maths en terminale corrigés en PDF.

Probabilités : exercices de maths en terminale corrigés en PDF.

Matrices : exercices en terminale spécialité de maths corrigés en PDF.

Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.

Représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.

Exercices de maths interactifs avec saisie au clavier des réponses.

Maths et programmation dans un escape game.

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Limite de fonctions : exercices de maths en terminale corrigés en PDF.

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

D'autres cours et exercices à consulter

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques