Intégrales et primitives : exercices de maths en terminale corrigés en PDF.
Mis à jour le 29 juillet 2025
Exercice 1 – Calcul intégral
Calculer

en cherchant une intégrale intermédiaire de la forme
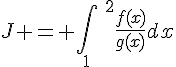
qui s’intégrera facilement.
Exercice 2 – Intégration par partie
Calculer ces intégrales en intégrant par parties:
A. 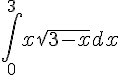 .
.
B.  .
.
C. 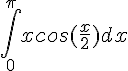 .
.
Exercice 3 – Dérivée d’une fonction
Soit  la fonction définie sur
la fonction définie sur 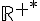 par
par 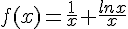 .
.
Quelle est la dérivée de  sur
sur 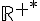 ?
?
Exercice 4 – Limite d’une fonction et asymptotes
Soit  une fonction définie sur
une fonction définie sur ![]-\infty,;0]\cup,[1;+\infty,[](https://mathovore.fr/latex-images/b24a30f3bdd80bbd2682eccc14d12b2c.png) tel que
tel que 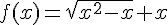 .
.
1. a. Déterminer la limite de  en
en  .
.
b. Déterminer la limite de  en
en 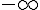 , que peut-on en déduire pour la courbe de
, que peut-on en déduire pour la courbe de  ?
?
2. Cette fonction est-elle dérivable en 0 ? en 1?
Que peut -on en déduire pour la courbe de  ?
?
3. a. Déterminer la limite en  de
de 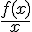 .
.
b. déterminer la limite en  de
de ![[f(x)-2x]](https://mathovore.fr/latex-images/4b62e01700f342ca4b48e52659a1911e.png)
En déduire que la courbe de  admet une asymptote oblique en
admet une asymptote oblique en  .
.
Exercice 5 – Fonction numérique et dérivée
Soit f la fonction définie sur 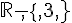 par
par 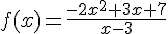
et C sa représentation graphique dans un repère orthonormé du plan.
1.a.Déterminer les limites de f en  et
et 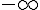 .
.
b.Etudier le comportement asymptotique de f en 3.Interpréter les résultats graphiquement.
2.a.Déterminer la dérivée de f et étudier les variations de f.Dresser le tableau de variation complet de f.
3.a.Montrer que la courbe de f admet la droite (D) d’équation y = – 2x – 3 comme asymptote oblique en  et
et 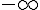 .
.
b.Déterminer algébriquement la position relative de la courbe C et de la droite (D).
4.Soit S(3;- 9).Montrer que S est le centre de symétrie de la courbe C.
Déterminer les coordonnées des points d’intersection de C avec l’axe des abscisses.
5. Construire la courbe C et y faire apparaître les éléments remarquables.
Exercice 6 – Intégrales et suites numériques au Bac S Liban
On considère la suite 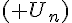 définie, pour tout entier naturel n , par :
définie, pour tout entier naturel n , par :
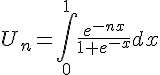
1.
a. Montrer que 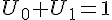 .
.
b. Calculer 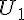 , en déduire
, en déduire 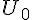 .
.
2. Montrer que, pour tout entier naturel n, 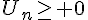 .
.
3.
a. Montrer que, pour tout entier naturel n non nul,

b. En déduire que, pour tout entier naturel n non nul,
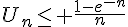
4. Déterminer la limite de la suite 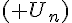 .
.
Exercice 7 – Intégrales et exponentielles Bac S Nouvelle Calédonie
Soit f la fonction définie pour tout nombre réel x par 
.
Le plan est rapporté à un repère orthonormal 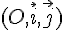 d’unité graphique 1 cm.
d’unité graphique 1 cm.
1. a. Étudier le signe de f(x) sur  .
.
b. Déterminer la limite de la fonction f en 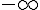 .
.
Déterminer la limite de la fonction f en  .
.
c. On note f ‘ la fonction dérivée de la fonction f sur  .
.
Calculer, pour tout nombre réel x, f'(x).
En déduire les variations de la fonction f sur  .
.
d. Tracer la courbe représentative de la fonction f sur l’intervalle [−2 ; 5].
2. On note 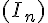 la suite définie pour tout entier naturel n par :
la suite définie pour tout entier naturel n par :
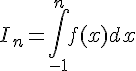
Dans cette question, on ne cherchera pas à calculer la valeur exacte de 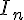 en fonction de n.
en fonction de n.
a. Montrer que, pour tout 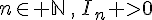 .
.
b. Montrer que la suite 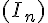 est croissante.
est croissante.
3. a. À l’aide d’une intégration par parties, montrer que pour tous réels a et b :

b. En déduire l’expression de 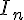 en fonction de n.
en fonction de n.
c. Déterminer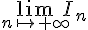 .
.
d. Donner une interprétation graphique de cette limite.
4. Déterminer  tel que
tel que
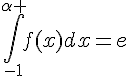 .
.
Ce calcul intégral correspond-il à un calcul d’aire ?
Exercice 8 – Dérivée
On considère la fonction numérique  définie sur
définie sur 
par  .
.
1. Calculer 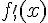 et
et  .
.
En déduire que 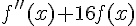 est constant .
est constant .
2. En déduire la valeur exacte de l’intégrale  .
.
Exercice 9 – Intégration par partie
Calculer :
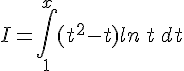
Exercice 10 – Le calcul de primitives
Etudier les primitives de la fonction f sur un intervalle I que l’on précisera .
a. 
b. 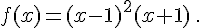
c. 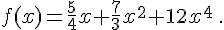
d. 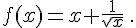
d. 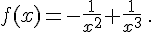
e. 
f. 
g. 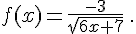
h. 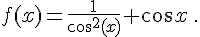
i. 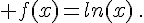
j. 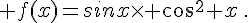
k. 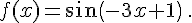
l. 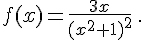
m. 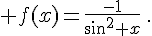
(Indication : penser à 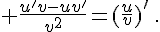 ).
).
Exercice 11
Déterminer la primitive F de la fonction f sur I vérifiant la condition indiquée.
a. 
b. ![f(x)=\frac{1}{sqrt{x}}-\frac{1}{x^2}\,,I=]0\,;\,+\infty[\,\,,F(1)=0\,.](https://mathovore.fr/latex-images/f44d9a29f333468c23977b8a5bed86cd.png)
c. 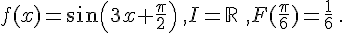
Exercice 12
Soit 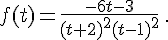
a. Déterminer deux nombres réels a et b tels que, pour tout t différent de -2 et 1,
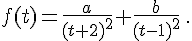
b. En déduire les primitives de f sur ]-2;1[ .
Exercice 13 – Extrait bac s sur l’intégration par partie
1. Déterminer trois réels a,b,c tels que , pour tout ![x\in ]0;+\infty[](https://mathovore.fr/latex-images/fd975fce6ace49e0aea4472e4348c527.png) :
:
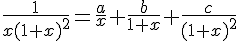 .
.
2. Soit 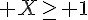 .
.
a. Calculer 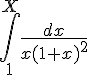 .
.
b. Soit f la fonction définie sur  par
par 
En intégrant par parties, calculer f(X) en fonction de X .
c. Montrer que 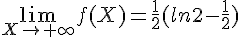
Exercice 14 – Les intégrales et les primitives
Calculer l’intégrale proposée :
a. 
b. 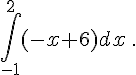
c. 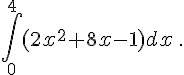
d. 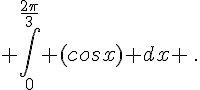
e. 
f. 
g. 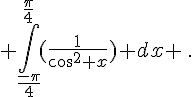
h. 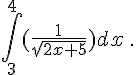
Exercice 15 – calculs d’aires
Soit 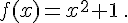
I=[-1;0].
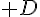 est délimité par l’axe des abscisse, la courbe
est délimité par l’axe des abscisse, la courbe 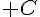 , les droites d’équations x=-1 et x=0 .
, les droites d’équations x=-1 et x=0 .
Démontrer que f est positive sur I et calculer l’aire du domaine 
Exercice 16 – propriétés de l’intégration
On considère  et
et 
a. Calculer 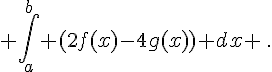
b. Déterminer 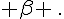 sachant que :
sachant que : 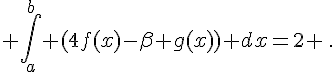
Exercice 17 – propriétés de l’intégration
Justifier sans calcul le résultat suivant :

Exercice 18
Calculer l’intégrale proposée en linéarisant :
a. 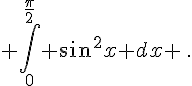
b. 
Exercice 19
Soit  .
.
a. Déterminer deux nombres réels a et b tels que, pour tout t différent de -2 et 1, 
b. En déduire les primitives de f sur ]-2;1[.
Exercice 20 :
Calculer la valeur des deux intégrales suivantes :

Exercice 21 :
f est la fonction définie sur  par
par 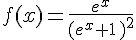 .
.
Pour chacune des fonctions définies ci-dessous, dire s’il s’agit d’une primitive de f sur  .
.
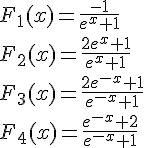
Exercice 22 :
Déterminer une primitive sur  des fonctions numériques suivantes :
des fonctions numériques suivantes :
![a)\,f(x)=5x^4-3x+7\,,\,I=\mathbb{R}\b)\,g(x)=4(3x-1)^5\,,\,I=\mathbb{R}\c)\,\,h(x)=\frac{7x}{x^2+4}\,,\,I=]-4;+\infty[\d)\,i(x)=3xe^x\,,\,I=\mathbb{R}](https://mathovore.fr/latex-images/ccef0e9d4c1224b964cb40f80c0fcaa8.png)
Exercice 23 :
a) Démontrer que pour tout réel t de l’intervalle [0;1],

b) Démontrer que, pour tout nombre réel t de l’intervalle 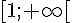

c) En déduire :
- un encadrement de

- l’inégalité
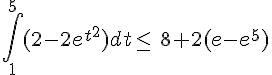
Exercice 24 :
Démontrer que pour tout entier naturel n,

Exercice 25 :
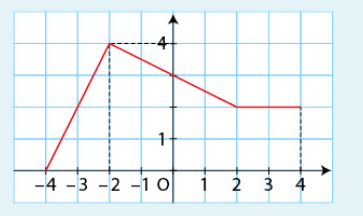
Dans le repère orthonormé ci-dessous, on a tracé la courbe représentative d’une fonction f définie
et continue sur l’intervalle [-4;4].
Calculer les intégrales suivantes :

Exercice 26 :
Calculer chacune des intégrales suivantes :
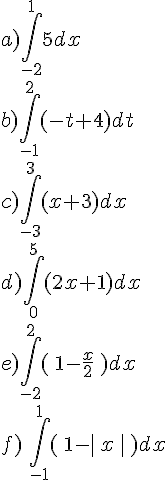
Exercice 27 :
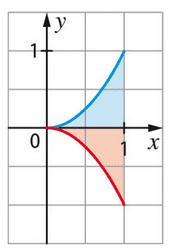
Sur le graphique ci- dessous sont tracées les courbes représentatives des
fonctions f et g définies sur [0 ; 1] par 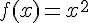 et
et 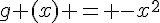 et deux surfaces
et deux surfaces
limitées par ces courbes.
1. Calculer l’aire, en unités d’aire, de la surface colorée en bleu.
2. En déduire, sans calcul, l’aire, en unités d’aire, de la surface colorée en rouge.
3. Retrouver l’aire précédente par un calcul d’intégrale.
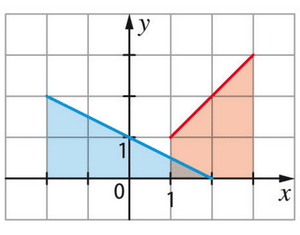
Pour l’exercice, indiquer si l’affirmation est vraie ou fausse, puis justifier.
Soit  et
et 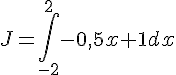 .
.
Par lecture graphique sur le schéma ci-contre I = J.
 par leurs expressions.
par leurs expressions.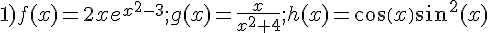 .
. .
.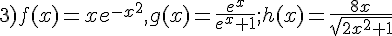 .
.Exercice 30 :
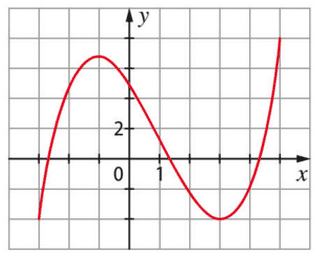
Soit une fonction f définie sur [ – 3 ; 5 ].
La courbe ci-dessous représente une primitive F sur [ – 3; 5 ] de f.
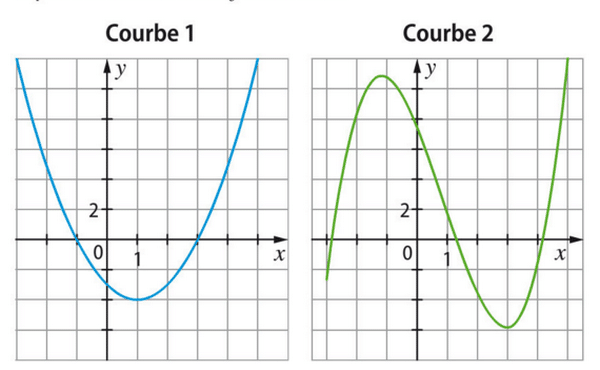
Parmi les deux courbes représentées ci-dessous, laquelle représente la fonction f? Justifier.
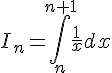 .
.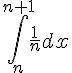 .
.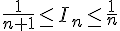 .
.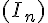 .
. par
par 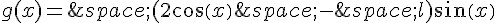 .
.Voici la courbe représentative de la fonction g dans un repère orthogonal.
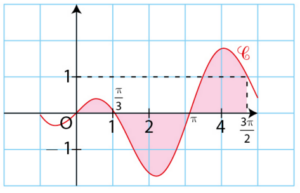
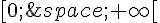 par :
par : 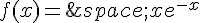 .
.On note
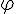 sa courbe représentative dans un repère orthogonal.
sa courbe représentative dans un repère orthogonal.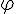 est au-dessus de l’axe des abscisses.
est au-dessus de l’axe des abscisses.b) Pour tout réel
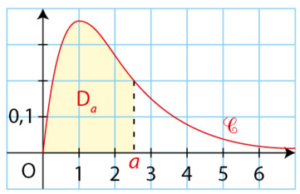
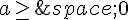 , on note
, on note 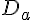 le domaine situé sous la courbe
le domaine situé sous la courbe 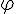 sur l’intervalle
sur l’intervalle ![[0;\,a]](https://mathovore.fr/latex-images/19809915284c507c1557201a07e94dfc.png) .
.A l’aide d’une intégration par parties, exprimer l’aire, en u.a., du domaine
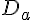 en fonction de a.
en fonction de a.c) Déterminer la limite de cette aire lorsque a tend vers
 .
.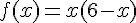 .
. est l’aire du domaine coloré, en unité d’aire.
est l’aire du domaine coloré, en unité d’aire.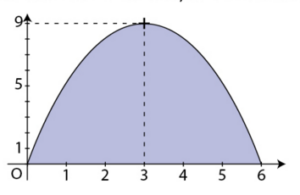
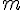 , on note
, on note 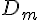 la droite d’équation
la droite d’équation 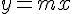 .
.Déterminer, si elles existent, les valeurs de
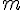 pour lesquelles l’aire du domaine compris entre
pour lesquelles l’aire du domaine compris entre 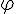 et
et 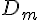 est égale à un huitième de
est égale à un huitième de 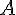 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «intégrales et primitives : exercices de maths en terminale corrigés en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.