Produit scalaire : exercices de maths en 1ère corrigés en PDF.

✏️Exercices

1ère • Lycée

Produit scalaire

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Le produit scalaire dans le plan avec des exercices de maths en 1ère en ligne pour progresser au lycée. Savoir appliquer les propriétés du produit scalaire et démontrer que des vecteurs sont orthogonaux ou colinéaires. Utiliser la relation de Chasles sur les vecteurs.

Exercice n° 1:
Soient $\vec{AB}$ et $\vec{AC}$ deux vecteurs et $k\in\mathbb{Z}$ .
Calculer $\vec{AB}.\vec{AC}$ dans les conditions suivantes :
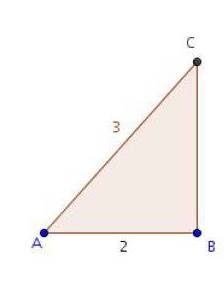
a. AB=3 , AC=5 et $(\vec{AB}.\vec{AC})=-\frac{\pi}{6}+2k\pi$ .
b. AB=1 , AC=4 et $(\vec{AB}.\vec{AC})=-\frac{8\pi}{3}+2k\pi$ .
c. AB=4 , AC=7 et $(\vec{AB}.\vec{AC})=-\frac{\pi}{4}+2k\pi$ .
d. AB=2 , AC=2 et $(\vec{AB}.\vec{AC})=-\frac{5\pi}{3}+2k\pi$ .

Exercice n° 2 :
Calculer $\vec{AC}.\vec{AB}\,;\,\vec{CA}.\vec{BA}\,;\,\vec{BA}.\vec{AC}\,\,;$ sachant que :
a. $\vec{AB}.\vec{AC}=-3$
b. $\vec{AB}.\vec{AC}=2$

Exercice n° 3 :
MNPQ est un losange de centre O tel que MP=8 et NQ=6.
Calculer les produits scalaires suivants :
a. $\vec{MO}.\vec{MN}\,;\,\vec{PQ}.\vec{NQ}\,;\,\vec{PM}.\vec{NP}\,\,;$ .
b. $\vec{MQ}.\vec{NP}\,;\,\vec{MN}.\vec{PQ}\,;\,\vec{OM}.\vec{NM}\,\,;$

Exercice n° 4 :
Soit ABCD un carré et I un point de [AB].
On note H le projeté orthogonal de A sur [ID].
En exprimant de deux manières différentes $\vec{IA}.\vec{ID}$ , démontrer que :
$\vec{IA}.\vec{ID}=AI^2$

Exercice n° 5 :
Soit ABC un triangle équilatéral de côté 1.
Soit H le projeté orthogonal de A sur (BC).
Calculer $\vec{BA}.\vec{AC}$ et $\vec{AB}.\vec{AH}$ en utilisant les projections orthogonales .

Exercice 6 – Produit scalaire dans un carré

Soit un carré ABCD. On construit un rectangle APQR tel que :

– P et R sont sur les côtés [AB] et [AD] du carré ;
– AP = DR.

Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.1. Justifier que : $\vec{CQ}.\vec{PR}=\vec{CQ}.(\vec{AR}-\vec{AP})$ .2. En déduire que les droites (CQ) et (PR) sont perpendiculaires.

Exercice 7 – Propriétés algébriques
On a $\| \vec{u} \right \|=2$ et $\| \vec{v} \right \|=3$ et $\vec{u$ . $\vec{v}$ = -1.
1) Calculez $(\vec{u}+\vec{v})^2$ et $\| (\vec{u} -\vec{v})^2\right \|$ .
2) Calculer ( $\vec{u}$ + $\vec{v}$ ) . (2 $\vec{u}$ -3 $\vec{v}$ ).

Exercice 8 – Produit scalaire et point quelconque
Soit A et B deux points distincts du plan et I le milieu du segment [AB].
Démontrer que quelque soit le point M du plan, on a l’égalité :
$MA^2-MB^2=(\vec{MA}+\vec{MB}).\vec{BA}=2\vec{MI}.\vec{BA}$ .

Exercice 9 – Les vecteurs dans le plan
Soit le parallélogramme ABCD tel que :
E est le milieu de [AD]
$\vec{AF}=\frac{2}{3}\vec{AB}$
K est le dernier sommet du parallélogramme EAFK
M le milieu de [BE]
$\vec{AG}=\frac{1}{3}\vec{AB}$
$\vec{GB}=2\vec{GF}$
$\vec{GC}=2\vec{GK}$

Montrer que vecteur $\vec{GK}=2\vec{GM}$ .

<Exercice 10 – Projeté orthogonal
ABC est un triangle rectangle en A .
H est le projeté orthogonal de A sur (BC) .
I et J sont les milieux respectifs de [AB] et [AC] .

Démontrer que (HI) et (HJ) sont perpendiculaires .

Exercice 11 – Calculs de produits scalaires dans un parallélogramme

ABCD est un parallélogramme avec AB = 4, AD = 5 et AC = 7.

1.Calculer $\vec{AB}.\vec{AD}$ .

2. En déduire BD.

Exercice 12 – Calculs de produits scalaires dans un carrés

MNPQ est un carré avec MN = 6. I est le centre du carré.y

Calculer les produits scalaires suivants :

1. $\vec{MN}.\vec{QP}$

2. $\vec{MN}.\vec{PN}$

3. $\vec{IN}.\vec{IP}$

4. $\vec{QI}.\vec{NI}$

Exercice 13 – Déterminer si le triangle est rectangle

ABC est un triangle dans lequel AB = 2 et AC = 3.

De plus $\vec{AB}.\vec{AC}=4$

Ce triangle est-il rectangle ? Si oui, préciser en quel sommet.

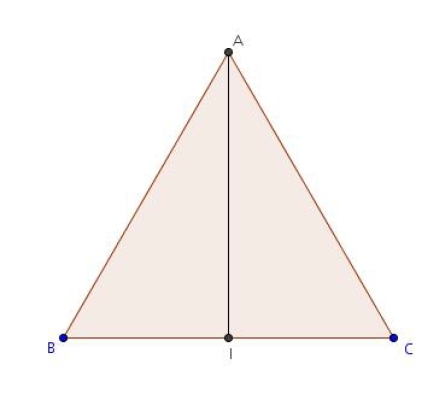
Exercice 14 – Triangle équilatéral
ABC est un triangle équilatéral de côté 5 cm. I est le milieu de [BC].

Calculer les produits scalaires suivants :

1. $\vec{BA}.\vec{BC}$ .

2. $\vec{CA}.\vec{CI}$

3. $(\vec{AB}-\vec{AC}).\vec{AI}$

Triangle
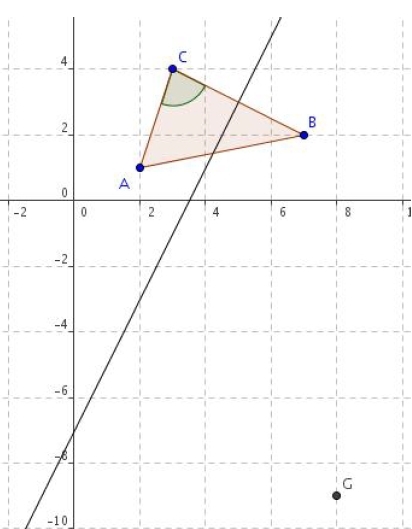
Exercice 15 – Coordonnées du barycentre

Dans un repère orthonormé $(O;\vec{i},\vec{j})$
on considère les points suivants : A (2 ; 1), B (7 ; 2) et C (3 ; 4).

Toutes les questions suivantes sont indépendantes et sans rapport.

1. Calculer les coordonnées du barycentre G de (A ; 3), (B ; 2) et (C ; – 4).

2. Déterminer une équation cartésienne de la médiatrice de [BC].

3. Calculer $\vec{CB}.\vec{CA}$ .

4. L’angle $\widehat{C}$ est-il droit ?

Exercice 16 – Cosinus
Soit ABC un triangle.
Calculer $\vec{AB}.\vec{AC}$ et $BC$ dans chacun des cas suivants :
1. AB= 6cm ; AC= 5 cm et $\widehat{BAC}=60^{\circ}$ .
2. AB= 7 cm ; AC=4cm et $\widehat{BAC}=120^{\circ}$ .

Exercice 17 – Vecteurs orthogonaux
$\vec{u}$ et $\vec{v}$ sont deux vecteurs de même norme .
Démontrer que les vecteurs $\vec{u}+\vec{v}$ et $\vec{u}-\vec{v}$ sont orthogonaux .

Exercice 18 – Triangle équilatéral
ABC est un triangle équilatéral de côté $a$ .
H est le projeté orthogonal de A sur (BC) et O le centre du cercle circonscrit à ABC.
Exprimer en fonction de $a$ , les produits scalaires suivants :
$\vec{AB}.\vec{AC}\,;\,\vec{AC}.\vec{CB}\,;\,\vec{AB}.\vec{AH}\,;\,\vec{AH}.\vec{BC}\,;\,\vec{OA}.\vec{OB}\,$ .

Exercice 19 – Calculs avec produits scalaires
Sachant que les vecteurs $\vec{u}$ et $\vec{v}$ sont tels que $\| \vec{u} \right \|=3$ , $\| \vec{v} \right \|=7$ et $\vec{u}.\vec{v} =13$ .
Calculer les produits scalaires suivants :
1. $\vec{u}.\left (\vec{u}+3\vec{v} \right )$ .
2. $(\vec{u}-2\vec{v} \right ) ^2$ .

Exercice 20 – Condition sur des points

A quelle condition sur les points A, B et C a-t-on :

$(\vec{AB}+\vec{AB})^2=(AB+AC)^2$

Exercice 21 – Déterminer un ensemble de points du plan

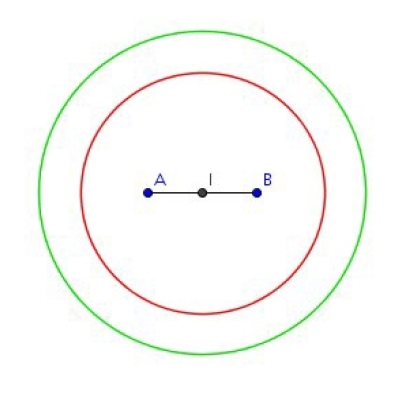
On considère un segment [AB] tel que AB = 1 dm.

Déterminer l’ensemble des points M du plan tels que :

1. $\vec{MA}.\vec{MB}=1$

2. $MA^2+MB^2=5$

Exercice 22 – Trouver un ensemble de points
[AB] est un segment de milieu I et AB = 2 cm.
1. Montrer que pour tout point M du plan :
$MA^2-MB^2=2\vec{IM}.\vec{AB}$
2. Trouver et représenter l’ensemble des points M du plan tels que : $MA^2 -MB^2 = 14$

Exercice 23 – Les égalités vectorielles du parallélogramme
Démontrer que :
1. $\| \vec{u}+\vec{v} \right \|^2-\left \| \vec{u}-\vec{v} \right \|^2=4\vec{u}.\vec{v}$ .
2. $\| \vec{u}+\vec{v} \right \|^2+\left \| \vec{u}-\vec{v} \right \|^2=2(\left \|\vec{u} \right \|^2+\left \| \vec{v} \right \|^2)$ .
3. Quel est le lien avec le losange, le parallélogramme ?
4. Démontrer que :
$(\vec{u}+\vec{v}).(\vec{u}-\vec{v})=\left \| \vec{u} \right \|^2-\left \| \vec{v} \right \|^2$
5. En déduire qu’un parallélogramme a ses diagonales perpendiculaires si et seulement si ses côtés sont égaux.

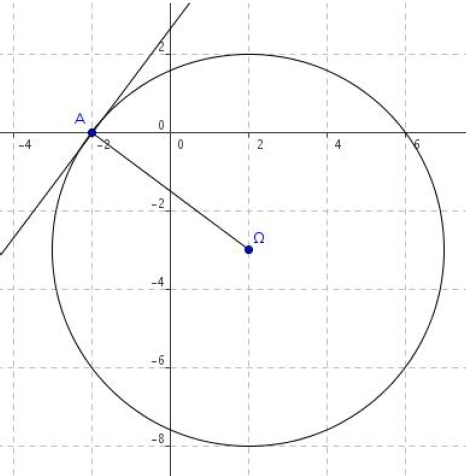
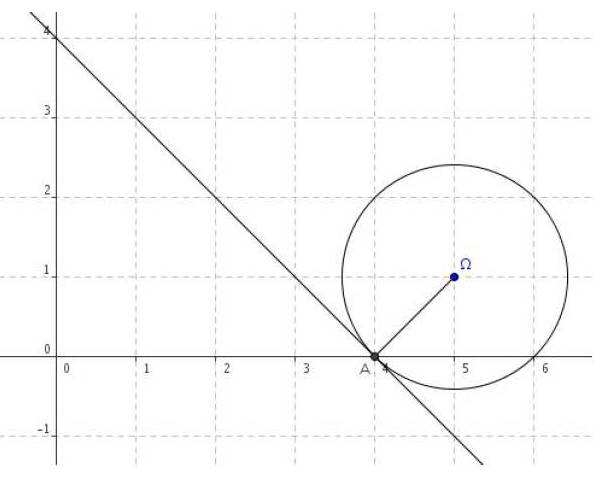
Exercice 24 – Equation d’un cercle et de la tangente

Dans un repère orthonormé $(O;\vec{i},\vec{j})$ , on donne un point $\Omega (2;-3)$ .

1. Déterminer l’équation du cercle (C) de centre $\Omega$ et de rayon R = 5.

2. Démontrer que le point A( – 2 ; 0) est un point du cercle (C).

3. Déterminer une équation cartésienne de la tangente en A au cercle (C).

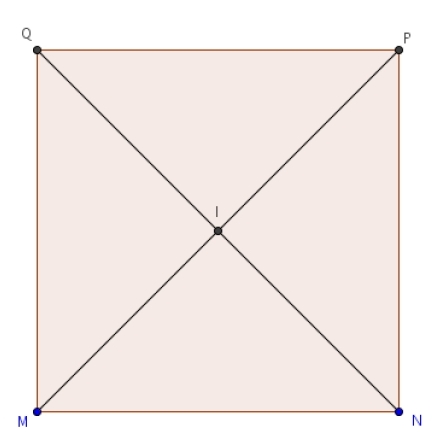
Exercice 25 – Médiatrice et hauteur d’un triangle
MNPQ est un carré avec MN = 6. I est le centre du carré.

Calculer les produits scalaires suivants :

1. $\vec{MN}.\vec{QP}$

2. $\vec{MN}.\vec{PN}$

3. $\vec{IN}.\vec{IP}$

4. $\vec{QI}.\vec{NI}$

Médiatrice et hauteur d'un triangle

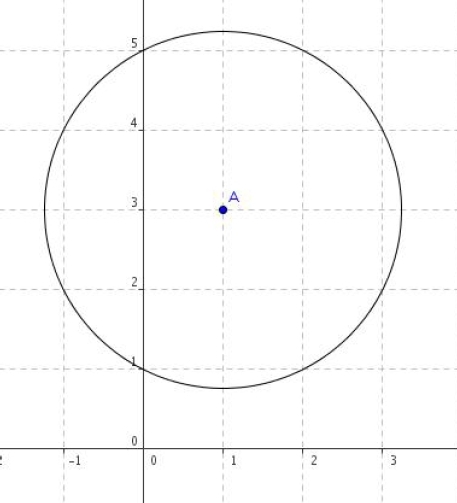
Exercice 26 – Distance d’un point à un cercle
On se place dans un repère orthonormé $(O;\vec{i},\vec{j})$ .
1. Déterminer l’équation du cercle de centre $\Omega (5;1)$ tangent à la droite (D) d’équation :
$x + y - 4 = 0$

Indication :

on rappelle que la distance entre un point $A(\alpha ;\beta )$ et une droite (D) d’équation ax + by + c = 0 est
donnée par la formule :

$d(A,D)=\frac{\left | a\alpha +b\beta +c \right |}{\sqrt{a^2+b^2}}$

Exercice 27 – Produit scalaire et cercle
On se place dans un repère orthonormé $(O;\vec{i},\vec{j})$ .

Examiner si les équations suivantes sont des équations de cercle et, le cas échéant, préciser le centre et le rayon du cercle.

1. $x^2 + y^2 - 2x - 6y + 5 = 0$

2. $x^2 + y^2 - x - 3y + 3 = 0$

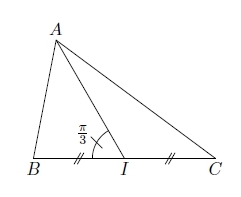
Exercice 28 – Produit scalaire dans un triangle

ABC est un triangle et I est le milieu de [BC].
On donne : BC = 4, AI = 3 et $(\vec{IA},\vec{IB})=\frac{\pi}{3}$ .

Calculer :

1. $\vec{AB}.\vec{AC}$

2. $AB^2+AC^2$

3. $AB^2-AC^2$

4. $AB\,et\,AC$

Exercice 29 :

On considère le carré ABCD de centre O et de côté 8.

Calculer les produits scalaires suivants.

$a)\vec{AB}.\vec{AO}$ $b)\vec{OB}.\vec{OD}$

$c)\vec{AB}.\vec{AD}$ $d)\vec{BO}.\vec{BC}$

Exercice 30 :

On considère les vecteurs $\vec{u}$ et $\vec{v}$ tels que $\left\|\vec{u}\right\|=2$ , $\left\|\vec{v}\right\|=3$ et $\widehat{(\vec{u} ,\vec{v})}=60^{\circ}$ .

Calculer leur produit scalaire.

Exercice 31 :

Déterminer une valeur en degrés de l’angle entre les vecteurs $\vec{u}$ et $\vec{v}$ tels que $\left\|\vec{u}\right\|=6$ , $\left\|\vec{v}\right\|=2$ et $\vec{u}.\vec{v} =-6$ .

Exercice 32 :

Soient les vecteurs $\vec{u} (-2;3 )$ et $\vec{v}(-1;-5)$ .

Calculer :

$a)\vec{u}.\vec{v}$ $b)(4\vec{u}).\vec{v}$ $c)(\vec{u}-\vec{v}).(\vec{u}+\vec{v})$

Exercice 33 :

On donne les points A(-3;-2) et B(1;3) et le vecteur $\vec{u}( -5;4 )$ .

Montrer que $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

Exercice 34 :

A,B,C et D étant des points quelconques du plan, montrer les égalités suivantes.

$a)\vec{AB}.\vec{CD}=\vec{BA}.\vec{DC}$ .

$b)\vec{AB}.\vec{AC}+\vec{AB}.\vec{EC}=\vec{AB}.\vec{ED}$

$c)\vec{AB}.\vec{AC}=\vec{AB}^2-\vec{BA}.\vec{BC}$

Exercice 35 :

On donne les points C et D tels que CD = 10 et H le milieu du segment [CD].

Déterminer l’ensemble des points M du plan vérifiant $\vec{MC}.\vec{MD}=-9$ .

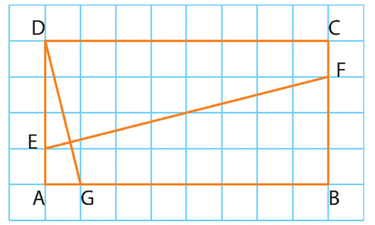
Exercice 36 :

Dans un rectangle ABCD de longueur 8 et de largeur 4, on place les points E, F et G tels que :

$\vec{AE}=\frac{1}{4}\vec{AD};\vec{AG}=\frac{1}{8}\vec{AB};\vec{CF}=\frac{1}{4}\vec{CB}$ .

1. Dans le repère (A ; G,E), donner les coordonnées de tous les points de la figure.

2. Calculer le produit scalaire $\vec{EF}.\vec{DG}$ .

3. Que peut-on en déduire ?

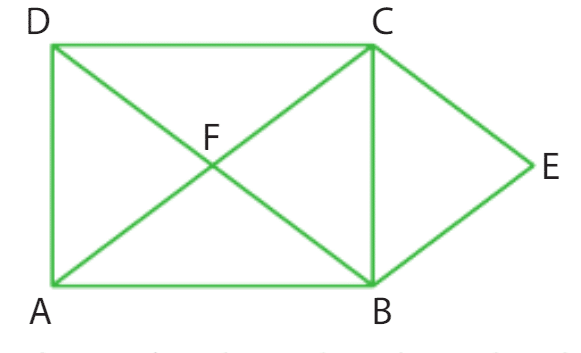
Exercice 37 :

ABCD est un rectangle de centre F et E est le symétrique du point F par rapport la droite
(BC). Calculer les produits scalaires suivants.

$a)\vec{BA}.\vec{BF}\,;b)\vec{CF}.\vec{CD}\,;c)\vec{AF}.\vec{AB}\,;d)\vec{AB}.\vec{BE}$

Exercice 38 :

Soient les vecteurs $\vec{u}(2;1)$ , $\vec{v}(-3;-1)$ et $\vec{w}(1;4)$ .

Calculer les produits scalaires suivants.

$a)\vec{u}.\vec{v}\\b)\vec{w}.\vec{v}\\c)\vec{u}.(\vec{v}+\vec{w})\\d)(-2\vec{u}).\vec{v}+3(\vec{v}.\vec{w})$

Exercice 39 :

On donne les vecteurs $\vec{u}(-3;4)$ et $\vec{v}(-8;-6)$ .

Montrer que ces vecteurs sont orthogonaux.

Exercice 40 :

Donner un vecteur directeur pour chacune des droites suivantes et en déduire qu’elles sont perpendiculaires.
a) Pour les droites d1 et d2 d’équations cartésiennes 2x-3y+4=0 et 3x+2y-1= 0.
b) Pour les droites d1et d2 d’équations cartésiennes x-y+3=0 et 2x+2y-1=0.
c) Pour les droites d1 et d2 d’équations y = —3x + 1 et -x+3y-1=0.

Exercice 41 :

Soient les vecteurs $\vec{u}(-2;3)$ , $\vec{v}(-1;-5)$ .

Calculer :

$a)\vec{u}.\vec{v}\\b)(4\vec{u}).\vec{v}\\c)(\vec{u}-\vec{v}).(\vec{u}+\vec{v})$

Exercice 42 :

Soient les vecteurs $\vec{u}(-3;4)$ , $\vec{v}(-8;-6)$ .

Montrer que ces vecteurs sont orthogonaux.

2. On donne les points A(-3;-2) et B(1;3) et le vecteur $\vec{u}(-5;4)$ .

Montrer que $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

Exercice 43 :

On considère les points A, B et C tels que AB = 3, AC = 4 et $\widehat{BAC}$ = 120°.

Déterminer la longueur BC.
2. On considère les points M, N et P tels que MN = 5, NP = 7 et MNP = 61°.

Déterminer la longueur MP.
3. Soit un triangle EFG tel que EF = 7, FG=6 et EG = 11.
Déterminer la valeur en degrés et arrondie à 0,1° de l’angle $\widehat{EFG}$ .
4. Soit un triangle EDF tel que EF = 5, DF = 8 et ED = 9.
Déterminer la valeur en degrés et arrondie à 0,1° de l’angle $\widehat{EDF}$ .

Exercice 44 :

soient les vecteurs $\vec{u}$ et $\vec{v}$ orthogonaux et tels que $\left \|\vec{u} \right \|=a$ et $\left \|\vec{v} \right \|=b$ .

Exprimer en fonction de a et de b les produits scalaires suivants.

$a)\vec{u}.(\vec{u}+\vec{v})\\b)(2\vec{u}-3\vec{v}).\vec{v}\\c)(\vec{u}+\vec{v})^2$

Exercice 45 :

Soit les vecteurs $\vec{u}$ ; $\vec{v}$ et $\vec{w}$ tels que : $\left \| \vec{u }\right \|=\left\|\vec{w } \right \|=a$ et $\vec{v}=3\vec{u}$ .

Les vecteurs $\vec{u}$ et $\vec{w}$ sont orthogonaux.

Exprimer en fonction de a les produits scalaires suivants.

$a)\vec{u}.\vec{v}\\b)\vec{v}.(\vec{u}+\vec{w})\\c)(\vec{u}+\vec{v})^2\\d)(\vec{v}+\vec{w}).(\vec{u}+\vec{w})$

Exercice 46 :

A, B, C et D étant des points quelconques du plan, montrer les égalités suivantes.
$a)\vec{AB}.\vec{CD} = BA.\vec{DC}\\b)\vec{AB}.\vec{CD}+\vec{AB}.\vec{EC}=\vec{AB}.\vec{ED}\\ c)\vec{AB} .\vec{AC}=\vec{AB} -\vec{BA }-\vec{BC}$

Exercice 47 :

1.On donne les points A et B tels que AB = 12 et I le milieu du segment [AB].

Déterminer l’ensemble des points M du plan vérifiant $\vec{MA} .\vec{MB} = 4$ .

2.On donne les points C et D tels que CD = 10 et H le milieu du segment [CD]. Déterminer l’ensemble des points M du plan vérifiant $\vec{MC}.\vec{MD }= - 9$ .

Exercice 48 :

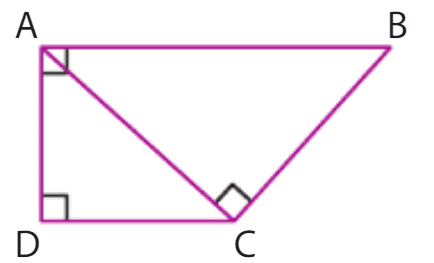
On considère un trapèze rectangle ABCD tel que la diagonale [AC] est perpendiculaire au côté [BC]. En calculant de deux manières le produit scalaire $\vec{AB}.\vec{ AC}$ , démontrer
que $AC^2 = AB\times CD$ .

Exercice 49 :

On considère deux carrés ABCD et BEFG disposés comme sur la figure
ci-dessous tel que AB = 1 et BE = a.

A. Avec coordonnées
1. Dans le repère (A ; B, D), donner les coordonnées de tous les points de la figure.
2. Démontrer que les droites (AG) et (CE) sont perpendiculaires.

B. Sans coordonnées
1. Développer le produit scalaire $(\vec{AB} + \vec{BG}). (\vec{CB} + \vec{BE})$ .
2. En déduire que $\vec{AG} .\vec{CE} = 0$ puis que les droites (AG) et (CE) sont perpendiculaires.

Exercice 50 :

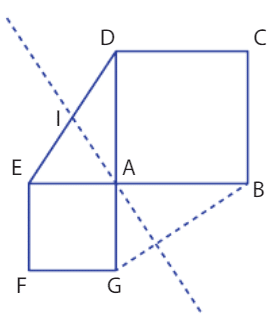
ABCD est un carré de côté a et AEFG est un carré de côté b avec D, A et G alignés, ainsi que B, A et E comme sur la figure ci-dessous.

Le point I est le milieu du segment [DE].

A. Sans coordonnées
1. Justifier que AD + AE = 2Al.
2. Développer le produit scalaire (AD + AE) . (BA + AG).
3. En déduire que les droites (AI) et (BG) sont perpendiculaires.

B. Avec coordonnées
1. Dans le repère (A ; B, D) donner les coordonnées des points A, I, B et G.
2. En déduire que les droites (AI) et (BG) sont perpendiculaires.

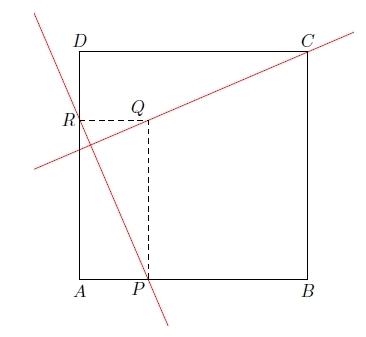
Exercice 51 :

On considère un carré ABCD de côté 1 et un point M quelconque sur le segment [BD]. On construit les projetés orthogonaux H et K du point M respectivement sur
les côtés [AB] et [AD].

1. On veut démontrer que les droites (CK) et (DH) sont perpendiculaires par deux méthodes :
a) On utilisera le repère (A ; B, D) et on notera (x;y) les coordonnées du point M.
b) On calculera le produit scalaire : $\vec{CK}.\vec{DH}$ en décomposant les vecteurs à l’aide de la relation de Chasles.
2. Démontrer que les longueurs CK et DH sont égales :
a) avec des coordonnées.
b) sans coordonnées.

5/5 - (23021 votes)

Produit scalaire : exercices de maths en 1ère corrigés en PDF.

Produit scalaire : exercices de maths en 1ère corrigés en PDF.

Trigonométrie : exercices de maths en 1ère corrigés en PDF.

Angles orientés et repérage polaire : exercices en 1ère corrigés | Première.

Les suites : exercices de maths en 1ère corrigés en PDF.