Equations et inéquations du second degré : cours de maths en 1ère en PDF.
Mis à jour le 1 septembre 2025
Dans tout ce chapitre, nous considérerons a un réel non nul.
I. Résolution de l’équation du second degré :
1. Définition et vocabulaire :
- Une équation du second degré, à une inconnue x, est une équation qui peut s’écrire sous la forme
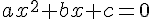 , où
, où 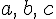 sont trois réels donnés avec
sont trois réels donnés avec 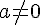 .
. - Résoudre l’équation
 , c’est trouver tous les nombres
, c’est trouver tous les nombres 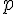 tels que
tels que 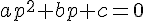 .
. - Un tel nombre p est dit solution ou encore racine de l’équation.
2. Résolution de l’équation du second degré :
Posons f(x) = ax²+bx+c avec 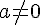 .
.
2.1. Ecriture de f(x) sous forme canonique :
Puisque 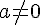 ,
, 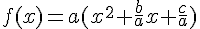 ou
ou 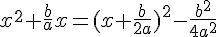
donc ![f(x)=a[(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2}]](https://mathovore.fr/latex-images/c6a934e071c8c23898d70da500e82485.png) .
.
Cette dernière écriture est appelée forme canonique de f.
2.2. Résolution de l’équation ax²+bx+c=0 :
On pose 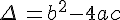 ainsi
ainsi ![f(x)=a[(x+\frac{b}{2a})^2-\frac{\Delta\,}{4a^2}]](https://mathovore.fr/latex-images/d865617072e5839321ad771ab07351ab.png)
Premier cas :
Si 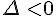 alors
alors 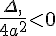 .
.
Le nombre entre crochets est strictement positif donc l’équation f(x)=0 n’a pas de solution.
Second cas :
Si 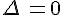 alors
alors 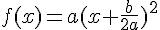 .
.
Puisque 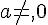 , l’équation f(x)=0 a une solution et une seule :
, l’équation f(x)=0 a une solution et une seule :
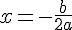 .
.
Troisième cas :
Si 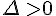 alors
alors 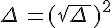 et :
et :
![f(x)=a[(x+\frac{b}{2a})^2-\frac{\Delta\,}{4a^2}]\,\f(x)=a[(x+\frac{b}{2a})^2-(\frac{\sqrt{\Delta}\,}{2a})^2]\,\f(x)=a(x+\frac{b}{2a}+\frac{\sqrt{\Delta}\,}{2a})(x+\frac{b}{2a}-\frac{\sqrt{\Delta}\,}{2a})](https://mathovore.fr/latex-images/d9bf9c9fed8ef055bfac8e9bd27f7f13.png)
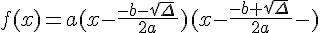
Si l’on pose :
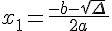 et
et 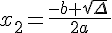 alors
alors 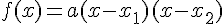 .
.
Donc puisque 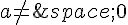 , l’équation f(x)=0 a deux solutions distinctes
, l’équation f(x)=0 a deux solutions distinctes 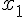 et
et 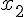 .
.
Le nombre 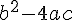 est appelé discriminant de l’équation du second degré
est appelé discriminant de l’équation du second degré 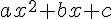 ou du trinôme
ou du trinôme 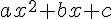 .
.
On le note 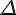 ( lire « delta »).
( lire « delta »).
a. Lorsque 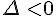 , l’équation n’a pas de solution dans
, l’équation n’a pas de solution dans  .
.
b. Lorsque 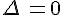 , l’équation a une racine double :
, l’équation a une racine double : 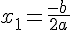 .
.
c. Lorsque 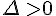 , l’équation a deux solutions :
, l’équation a deux solutions :
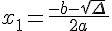 et
et 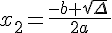 .
.
II. Factorisation et signe du trinôme :
1. Factorisation du trinôme :
Nous avons vu, au cours de la démonstration du théorème 1 que si
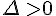 alors
alors 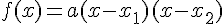 .
.
Lorsque l’équation f(x)=ax²+bx+c=0 a deux solutions 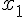 et
et 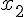 ( dans le cas
( dans le cas 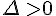 ) alors,
) alors,
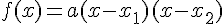
2. Signe du trinôme :
- Lorsque
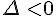 ,
, 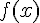 est toujours du signe de a.
est toujours du signe de a. - Lorsque
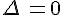 ,
, 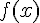 est du signe de a
est du signe de a - Lorsque
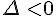 ,
, 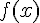 est du signe de a, sauf lorsque x est entre les racines, auquel cas f(x) et a sont de signes contraires.
est du signe de a, sauf lorsque x est entre les racines, auquel cas f(x) et a sont de signes contraires.
Application :
Pour résoudre une inéquation du second degré, on détermine le signe du trinôme associé.
III. Représentations graphiques des fonctions trinômes :
La courbe de la fonction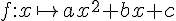 est une parabole. Cette parabole est tournée vers le haut lorsque
est une parabole. Cette parabole est tournée vers le haut lorsque  et tournée vers le bas lorsque
et tournée vers le bas lorsque 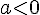 .
.
Synthèse :
Exemples :
Résoudre 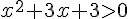
Solution :
 puisque
puisque 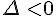 , le trinôme n’a pas de racine dans
, le trinôme n’a pas de racine dans  .
.
De plus a=1 donc a>0 ainsi 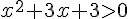 pour tout
pour tout  réel et
réel et 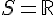 .
.
Résoudre l’inéquation du second degré  .
.
Nous avons 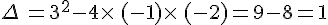 .
.
L’équation 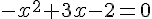 a deux racines qui son t:
a deux racines qui son t:
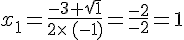
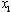
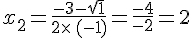 .
.
Nous avons  donc
donc 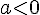 ainsi l’ensemble solution de l’inéquation du second degré
ainsi l’ensemble solution de l’inéquation du second degré  est l’intervalle
est l’intervalle ![[1\,;2]](https://mathovore.fr/latex-images/6e505d2bf49e756e50f7b896e04e9aeb.png) .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «equations et inéquations du second degré : cours de maths en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
Exercices de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.


















