Sommaire de cette fiche
Les tableaux ci-dessous résument les résultats à connaître.
Ces tableaux sont valables dans les trois situations étudiées:
- Lorsque la variable
.
- Lorsque la variable
.
- Lorsque la variable
où a
R.
Mais il va de soi que, pour les deux fonctions f et g concernées, les limites sont prises au même endroit!
Dans le cas particulier où les fonctions sont des suites numériques, on peut utiliser ces résultats en remplaçant f par (Un) et g par (Vn) avec le seul cas envisageable la variable .
Les conventions utilisées dans ces tableaux, sont:
· et
désignent des nombres réels ( limites finies ).
· ? indique que dans la situation concernée, on n’a pas de conclusion générale.
On dit parfois qu’il s’agit d’une « forme indéterminée » notée F.I.
Il faudra dans ces cas, mettre au point d’autres méthodes de résolution.
I. Limite d’une somme de deux fonctions
II. Limite d’une différence de deux fonctions
Utiliser : f – g = f + (-g) et le tableau précédent.
III. Limite d’un produit de deux fonctions
IV. Limite de l’inverse d’une fonction
Dans le tableau ci-dessous, la limite de f égale à , signifie, qu’à l’endroit où la limite est prise, cette limite est zéro et que, pour tout x suffisamment proche de cet endroit, on a f(x) > 0.
Définition analogue pour , mais avec f(x) < 0.
V. Limite d’un quotient de deux fonctions
On peut utiliser: et avec les deux tableaux précédents, il est possible de conclure.
En + ou en –
, la limite d’une fonction rationnelle est la limite du quotient des termes de plus haut degré du numérateur et du dénominateur.
On peut aussi retenir les résultats suivants :
Ce tableau est simplifié: ± signifie +
ou bien –
.
Pour décider, on applique la règle du signe du quotient selon les signes de f et de g au voisinage de l’endroit où la limite est cherchée.
VI. Limite des fonctions de références.
VII. Le théorèmes de comparaison
Pour les fonctions, dans les propriétés ci-dessous, la lettre a désigne aussi bien un réel que + ou –
.
Lorsque a = + , les fonctions sont définies sur R ou un intervalle I de la forme [ A ; +
[ où A est un réel.
Lorsque a = – , les fonctions sont définies sur R ou un intervalle I de la forme ] –
; A ] où A est un réel.
Lorsque a R , les fonctions sont définies sur R ou un intervalle I de la forme [ A ; B ] où A et B sont des réels et a
[ A ; B ].
Si la limite concernée est la limite à gauche de a, les fonctions sont définies sur un intervalle I de la forme ] – ; a [ ou [ A ; a [ où A est un réel.
Si la limite concernée est la limite à droite de a, les fonctions sont définies sur un intervalle I de la forme ] a ; + [ ou ] a ; A ] où A est un réel.
Pour les suites, l’indice n est un entier naturel supérieur ou égal à un certain rang (qui sera souvent 0).




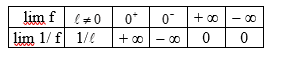
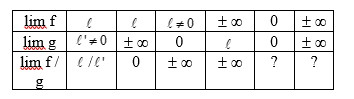




 Mathovore c'est 13 931 277 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 277 cours et exercices de maths téléchargés en PDF.
Je veux bien la correction du livre de physique chimie en première