Exercice 1 :
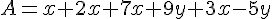
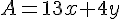
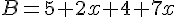
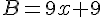
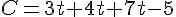
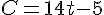
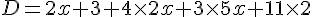
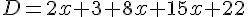
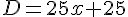
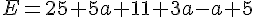
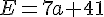
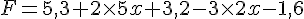
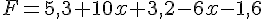
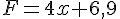
Exercice 2 :
Soit l’expression 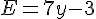 .
.
Calculer la valeur de E pour :
a) 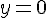 ;
;
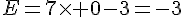
b) 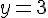 ;
;
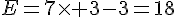
c) 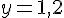 .
.
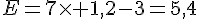
Exercice 3 :
A = 13xz= 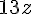
B= 4×5 = 20
C= (4-  )x3=
)x3= 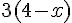
D= 4xaxb= 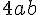
E = axb+7x  +5=
+5= 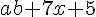
F=5x(  +3)=
+3)= 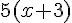
G=  x(y+2)=
x(y+2)= 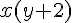
Exercice 4 :
Première façon :
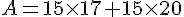
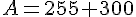
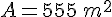
Deuxième façon :
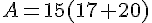
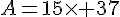
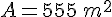
Exercice 5 :
a) 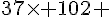
=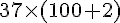
=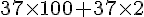
=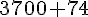
=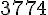
b) 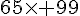
=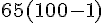
=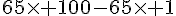
= 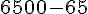
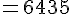
Exercice 6 :
Calculer l’expression suivante pour 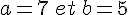 :
:
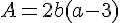
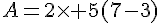
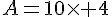
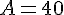
Exercice 7 :
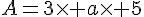
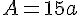
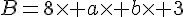
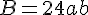
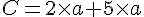
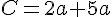
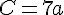
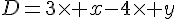
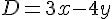
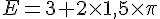
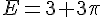
Exercice 8 :
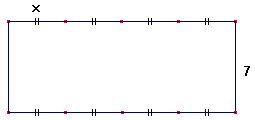
1. Exprimer la longueur du rectangle en fonction de  .
.
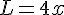
2. Exprimer le périmètre du rectangle en fonction de  .
.
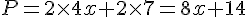
3. Calculer le périmètre lorsque :
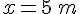
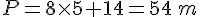
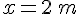
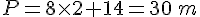
Exercice 9 :
a) Écrire en fonction de x le prix d’un CD.
x+2
b) Écrire en fonction de x les prix d’un livre.
x+4
c) Paul achète 4 CD , écrire en fonction de x le montant de ses achats.
4(x+2)=4x+8
d) Louise achète 2 BD et 2 livres , écrire en fonction de x le montant de ses achats.
2x+2(x+4)=2x+2x+8=4x+8
e) Montrer que Paul et Louise ont dépensé la même somme.
Ils ont bien la même dépense qui correspond à 4x+8 .
Exercice 10 :
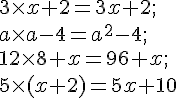
Exercice 11 :
Une clé USB coûté x euros et un livre coûte 5 € de plus.
1. Quel est le prix de 3 livres ?
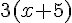
2. Quel est le prix de 2 Clés USB et 4 livres ?
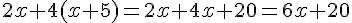

Exercice 12 :
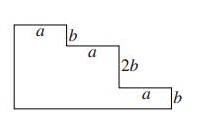
Exercice 13 :
La longueur de gauche est b+2b+b=4b .
La longueur du bas est a+a+a=3a .
La longueur de l’escalier est a+b+a+2b+a+b=3a+4b .
Le périmètre est 4b+3a+3a+4b=6a+8b
Conclusion : la réponse est E .
A) 3a+4b .
B) 3a+8b
C) 6a+4b
D) 6a+6b
E) 6a+8b
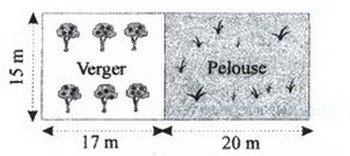
Exercice 14 :
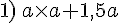
L’aire totale du rectangle .
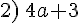
Le périmètre du rectangle .
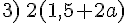
Le périmètre du rectangle .
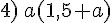
L’aire du rectangle .
Exercice 15 :
|
Expression |
Réponse A |
Réponse B |
Réponse C |
|
|
1 |
8 (a + 3) |
8 a + 3 |
8 a + 24 |
8 a + 83 |
|
2 |
5 (x – 9) |
5 x + 45 |
5 x – 9 |
5 x – 45 |
|
3 |
k (a + 9) |
a + 9 k |
k a + 9 |
k a + 9 k |
|
4 |
|
4 |
4 |
4 |
Exercice 16 :
Julie a écrit :
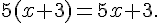
Marc a écrit :
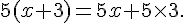
Sonia a écrit :
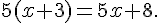
Lequel de ces trois élèves a distribué correctement 5 ?
Marc a distribué correctement.
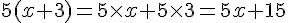
Exercice 17 :
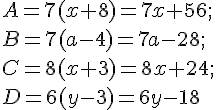
Exercice 18 :
Pour x = 1 , effectue les calculs suivants :
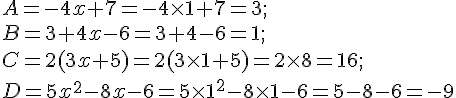
Exercice 19 :
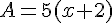
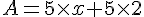

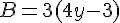
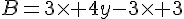
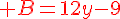
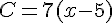
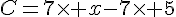
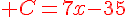
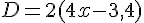
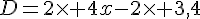
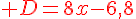
Le calcul littéral en 5ème est un chapitre très important pour la progression de l’élève en Maths. En effet, ce corrigé vous permettra de développer de nouvelles compétences et de bien maîtriser le calcul littéral en 5ème. Lisez l’énoncé avant de commencer les exercices. Cela vous permettra d’avoir un bon aperçu et d’éviter de faire des erreurs lors de la résolution . Appliquez les propriétés apprises en classe.
Exercice 20 :
Réduire (si possible) et supprimer les signes × :
A = 5 × x × y=5xy
B = 3 × 6 × x=18x
C = 6 + 10 × x=6+10x
D = 7 × x × y × 2=14xy
E = 3 × x × x=3x²
F = 3 × x + 5 × y=3x+5y
G = 5 × x × x × 3=15x²
![K = [(a / 4) + (b \times 2)]=\frac{a}{4}+2b](https://mathovore.fr/latex-images/cdf13c930a3043f9d8017bf45d9453e0.png)
L = 3 × a × b × a – c × 4 × a=3a²b-4ac
M = 2 × (3 × x × 2 × y)=12xy
N = 8 × a + 15 × a – 3 × a=8a+15a-3a=20a
O = 19 x – 13 x + 11 x=17x
P = 4 × b × 9 + 4 × a × a − c × 3=36b+4a²-3c
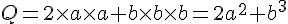
Exercice 21 :
Sachant que x = 8 ; y = 5 et z = 1 calculer :
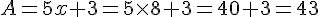
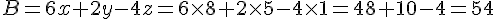
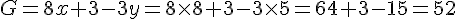
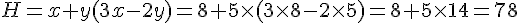
Exercice 22 :
Développer puis réduire :
A = 8 (x – 3)=8x-24
B = 5 (2 x − 6)=10x-30
C = 3 x (2 x − 7)=6x²-21x
G = 4 (2 x + 5) + 3 (x − 6)=11x+2
H = 2 (3 x + 4 y – 2)=6x+8y-4
I = 2 x (x + 1) + x (5 x − 2)=7x²
J = 2 (3 x + 5) + 4 (2 x + 3)=14x+22
Exercice 23 :
Calculer de deux façons différentes :
A = 3 × 5 + 3 × 2=3x(5+2)=3×7=21 ou A=15+6=21
B = 6 × 2 − 5 × 2=2x(6-5)=2×1=2 ou B =12-10=2
C = 4 (5 − 3)=4×5-4×3=20-12=8 ou C= 4×2=8
D = 4 × 5 + 4=4x(5+1)=4×6=24 ou D=20+4=24
Exercice 24 :
Calculer astucieusement :
A = 45 × 99=45x(100-1)=45×100-45×1=4 500-45=4 455
B = 2,7 × 3,6 + 2,7 × 6,4=2,7x(3,6+6,4)=2,7×10=27
C = 18 × 101=18x(100+1)=18×100+18×1=1 800 + 18= 1818


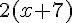
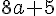
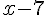
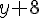

 (4 + R)
(4 + R)