Les équations et problèmes : corrigé des exercices en 3ème.

Le corrigé des exercices de maths en 3ème sur la résolution des équations du premier degré à une inconnue. Savoir résoudre une équation et déterminer son ensemble solution en troisième.

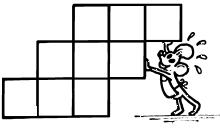
Exercice 1 :

Exercice 2 :

Déterminer trois nombres entier positifs consécutifs dont la somme des carrés est égale à 1 325.

Pour la facilité des calculs on choisira les nombres consécutifs suivants :

n-1 ; n ; n +1 avec n $\in \mathbb{N}$

1- Calcul des carrés des nombres n-1 et n+1

(n-1)² = n² -2n +1

(n+1)²= n² +2n +1

2- Calcul de la somme des carrés des trois nombres.

(n-1)² + n² + (n+1)² = 3n² + 2

3- Puisque cette somme est égale à 1325, on est conduit à résoudre l’équation :

3n² +2 = 1325

soit

3n² = 1323

n² = 441

n= $\sqrt{441}$ = 21

Vérification:

n-1 = 20

n = 21

n+1 =22

20² +21² +22² = 400 +441 + 484 = 1325

Donc les nombres consécutifs à déterminer sont : 20 ; 21 ; 22

Exercice 3 :

Trois club se rencontrent lors d’une compétition. Le club A remporte un tiers des médailles , le club B deux septième des médailles et le club C seize médailles . Combien de médaille ont été distribuée en tout ?

Soit $x$ : le nombre de médailles remportées .

les club A et B ont remportés : $\frac{1}{3}+\frac{2}{7}=\frac{7}{21}+\frac{6}{21}=\frac{13}{21}$ des médailles .

Le club C a donc remporté $\frac{8}{21}$ des médailles soit 16 médailles .

donc $\frac{8}{21}x=16$

$x=\frac{16\times 21}{8}$

$x=42$

Conclusion : il y a eu 42 médailles de distribuées .

Exercice 4 :

Résoudre les équations suivantes :

1. (x-7)²-(2x+5)²=0

$(x-7-2x-5)(x-7+2x+5)=0$

$(-x-12)(3x-2)=0$

Propriété : un produit de facteurs est nul si et seulement si un des facteurs, au moins, est nul .

$-x-12=0\,\,ou\,\,3x-2=0$

$x=-12\,\,ou\,\,x=\frac{2}{3}$

2. (7x+1)²-(3x+4)²=0

$(7x+1-3x-4)(7x+1+3x+4)=0$

$(4x-3)(10x+5)=0$

$4x-3=0\,\,ou\,\,10x+5=0$

$x=\frac{3}{4}\,\,ou\,\,x=-\frac{5}{10}$

$x=\frac{3}{4}\,\,ou\,\,x=-\frac{1}{2}$

3. (6x-1)²-(2x+1)²=0

$(6x-1-2x-1)(6x-1+2x+1)=0$

$(4x-2)\times 8x=0$

$4x-2=0\,\,ou\,\, 8x=0$

$x=\frac{2}{4}\,\,ou\,\, x=0$

$x=\frac{1}{2}\,\,ou\,\, x=0$

Exercice 5 :

une tirelire contient 65 euros en pièces de 1 € et 2 € au total de 35 pièces .

Combien y a t il de pièces de 1 euros et combien de 2 euros ?

Soit x le nombre de pièces de 1 € et y le nombre de pièces de 2 € .

x+y=35 (1)

x+2y=65 (2)

En faisant la soustraction de (2)-(1) :

x+2y-x-y=65-35

y=30

Il y a donc 30 pièces de 2 € et 5 pièces de 1 € .

Exercice 6 :
a. 3x + 2 = 14
3x=14-2
3x=12
x=12:3
x=4
donc S={ 4 }

b. 3x – 4 = 2x + 9
3x-2x=9+4
x=13

c. 5x – 4 = 8 – 3x
5x+3x=8+4
8x=12
x=12:8=3:2
donc S={ 1,5 }

d. 3 – (5 – x) = 3 – 4x
3-5+x=3-4x
-2+x=3-4x
x+4x=3+2
5x=5
x=5:5=1
donc S={ 1 }

e. 2x + 5 = 3x – 1
2x-3x=-1-5
-x=-6
x=6
donc S={ 6 }

f. 2(5 – 3x) = 6(2x + 1)
10-6x=12x+6
-6x-12x=6-10
-18x=-4
x=4:18=2:9
donc S={ 2:9 }

g. 4(3x – 2) – 10x = 3x – 1
12x-8-10x=3x-1
2x-8=3x-1
2x-3x=8-1
-x=7
x=-7
donc S={ -7 }

h. 3(x + 2) – (x – 3) = x – 5 – 3(x + 1) + 4x
3x+6-x+3=x-5-3x-3+4x
2x+9=2x+2
0x=2-9
0x=-7
0=-7
absurde donc pas de solution.

i. 5x + 7 = -5 + 11x
5x-11x=-5-7
-6x=-12
x=12:6=2
donc S={ 2 }

j. 2x + 1 = 4(x – 2) + x
2x+1=4x-8+x
2x-4x-x=-1+8
-3x=7
x=-7:3
donc S={ -7:3 }.

Exercice 7 :

$7x-1=-3x+2$
$7x+3x=2+1$
$10x=3$
$x=\frac{3}{10}$

Exercice 11 :

Résolvez les équations suivantes :

1) $5x+2=2x+6$

$5x-2x=6-2$

$3x=4$

${\color{DarkRed} x=\frac{3}{4}}$

2) $2(3x+3)=-2(x-7)$

$6x+6=-2x+14$

$6x+2x=14-6$

$4x=8$

${\color{DarkRed} x=\frac{8}{2}}$

3) $-3(4x+3)=2x+6$

$-12x-9=2x+6$

$-12x-2x=6+9$

$-14x=15$

${\color{DarkRed} x=-\frac{15}{14}}$

4) $\frac{x+3}{3}=\frac{2x+1}{4}$

$4(x+3)=3(2x+1)$

$4x+12=6x+3$

$4x-6x=3-12$

$-2x=-9$

${\color{DarkRed} x=\frac{9}{2}}$

5) $\frac{2x-3}{3}=-5x+1$

$2x-3=3(-5x+1)$

$2x-3=-15x+3$

$2x+15x=3+3$

$17x=6$

${\color{DarkRed} x=\frac{6}{17}}$

6) $\frac{3-4x}{5}=\frac{2x+1}{4}$

$4(3-4x)=5(2x+1)$

$12-16x=10x+5$

$-16x-10x=5-12$

$-26x=-7$

${\color{DarkRed} x=\frac{7}{26}}$

Exercice 12 :

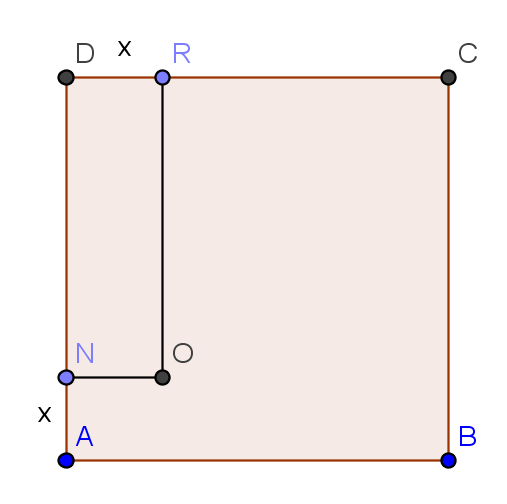
Soit ABCD est un carre de cote 10 cm . N est un point de [AD] et R est un point de [DC] tels que AN est égal a DR est egal a x (en cm).
On souhaite trouver la position du point N pour laquelle l aire du rectangle NORD est maximale .
1) Donner un encadrement de x.

$0\leq x\leq 10$ 2)a) Exprimer l’aire de NORD en fonction de x.

$A_{NORD}=x(10-x)$

b) Démontrer que l’ aire est egale a : 25-(x-5)².

$25-(x-5)^2=25-(x^2-10x+25)=-x^2+10x=x(10-x)=A_{NORD}$ 3)a) Déterminer la valeur de x pour laquelle l aire NORD est maximale où est alors situé le point N .

L’aire est maximale lorsque la quantité $(x-5)^2$ est minimale c’est à dire lorsque $x=5$ .

N est donc situé au milieu de [AD] .

b) Dans ce cas que peut on dire du rectangle NORD .

Dans ce cas NORD est un carré .

Exercice 13 :

a. 3x + 2 = 14

3x=14-2
3x=12
x=12:3
x=4
donc S={ 4 }

b. 3x – 4 = 2x + 9
3x-2x=9+4
x=13

c. 5x – 4 = 8 – 3x
5x+3x=8+4
8x=12
x=12:8=3:2
donc S={ 1,5 }

d. 3 – (5 – x) = 3 – 4x
3-5+x=3-4x
-2+x=3-4x
x+4x=3+2
5x=5
x=5:5=1
donc S={ 1 }

e. 2x + 5 = 3x – 1
2x-3x=-1-5
-x=-6
x=6
donc S={ 6 }

f. 2(5 – 3x) = 6(2x + 1)
10-6x=12x+6
-6x-12x=6-10
-18x=-4
x=4:18=2:9
donc S={ 2:9 }

g. 4(3x – 2) – 10x = 3x – 1
12x-8-10x=3x-1
2x-8=3x-1
2x-3x=8-1
-x=7
x=-7
donc S={ -7 }

h. 3(x + 2) – (x – 3) = x – 5 – 3(x + 1) + 4x
3x+6-x+3=x-5-3x-3+4x
2x+9=2x+2
0x=2-9
0x=-7
0=-7
absurde donc pas de solution.

i. 5x + 7 = -5 + 11x
5x-11x=-5-7
-6x=-12
x=12:6=2
donc S={ 2 }

j. 2x + 1 = 4(x – 2) + x
2x+1=4x-8+x
2x-4x-x=-1+8
-3x=7
x=-7:3
donc S={ -7:3 }

Exercice 14 :

En multipliant par 6 les deux membres de l’équation,
on obtient :

Exercice 15 :
1. (x + 5)(x – 3) = 0
C’est une équation produit, on utilise donc la règle :
« un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul »
ainsi:
x+5 = 0 ou x-3 = 0
x= -5 ou x=3
donc S = {-5 ; 3}

2. ( 2x + 7 )( -5x + 2 ) =0
On utilise la règle.
2x+7=0 ou -5x+2=0
2x=-7 ou -5x=-2
x=-7:2 ou x = -2:(-5)=2:5
donc S = {-3,5 ; 0,4}

3. 64x² – 81 = 0
il fallait reconnaitre l’identité remarquable.
(8x)²-9²=0
(8x+9)(8x-9)=0
on utilise la règle.
8x+9=0 ou 8x-9 = 0
x= -9:8 ou x= 9:8
donc S= { -9:8 ; 9:8}

5. ( 3 – x )(2x + 7 )(-5 + x) = 0
On utilise la règle qui est valable pour deux facteurs d’ailleurs également pour n facteurs.
3-x=0 ou 2x+7 = 0 ou -5+x=0
x=3 ou x=-7:2 ou x=5
donc S={3 ; -3,5 ; 5 }

6. 49X² – 42X + 9 = 0
il fallait reconnaitre l’identité remarquable.
(7X)²-2x7Xx3+3²=0
(7X-3)² = 0
(7x-3(7x-3)=0
On utilise la règle.
7x-3=0
x=3:7
donc S ={3:7}
Exercice 16:
Trouver les équations qui admettent ( 2 ) pour solution:

1. 2x + 4 = 0
remplaçons x par -2 dans l’équation.
2x+4=2x(-2)+4=-4+4=0
donc -2 vérifie bien l’égalité donc -2 est solution de l’équation..
2. 2x =- 4
remplaçons x par -2 dans l’équation.
-2x=-2x(-2)=+4 -4
donc -2 ne vérifie pas l’égalité donc -2 n’est pas solution de l’équation..

3. 6x + 2 = 10
6x+2=6x(-2)+2=-12+2=-10
donc -2 vérifie bien l’égalité donc -2 est solution de l’équation..

4. 5x + 4 = 2x+3
remplaçons x par -2 dans l’équation.
-5x+4=-5x(-2)+4=10+4=14 et 2x+3=2x(-2)+3=-4+3=-1
or 14 -1
donc -2 ne vérifie pas l’égalité donc -2 n’est pas solution de l’équation..
Exercice 17 :
1. Choix de l’inconnue :
Notons x :l’ âge de Julie.

2. Traduction mathématique de l’énoncé:
sa mère était âgée de 30 ans donc l’âge de sa mère est: x+30;
son frère avait 4 ans donc l’âge de son frère est: x+4

3. Mise en équation du problème :
Julie, son frère et sa mère totalisent un siècle
donc x+ (x+30) + (x+4) = 100
x+x+30+x+4=100
3x+34=100
3x=100-34
3x=66
x=66:3
x=22

Conclusion : Julie a 22 ans, sa mère en a 52 ans et son frère a 26 ans.

Exercice 18 :

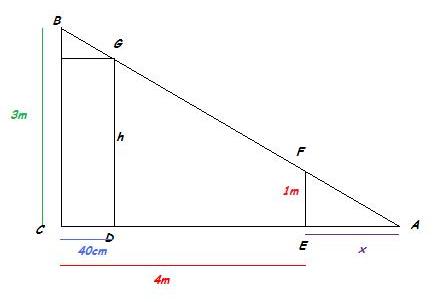
Trouver la longueur x.

Dans les triangles AEF et ACB ,

$\left \{ F \in (AB)\\E\in (AC) \\(FE)//(BC)\right.$ d’après la partie directe du théorème de Thalès :

$\frac{AE}{AC}=\frac{EF}{BC}$

$\frac{x}{x+4}=\frac{1}{3}$

$3x=1\times (x+4)$

$3x=x+4$

$3x-x=4$

$2x=4$

$x=\frac{4}{2}$

${\color{DarkRed} x=2\,m}$

Exercice 19 :

Résoudre les équations suivantes après avoir factoriser a l’aide d’une identité remarquable: a) x² +14x+49=0

$(x+7)^2=0$

${\color{DarkRed} x=-7}$ b) y²-12y+36=0

$(y-6)^2=0$

${\color{DarkRed} y=6}$ c) 4x²-20x +25=0

$(2x-5)^2=0$

$2x-5=0$

${\color{DarkRed} x=\frac{5}{2}}$
d) 24z+16+9z²=0

$(3z+4)^2=0$

$3z+4=0$

${\color{DarkRed} z=-\frac{4}{3}}$

Exercice 20 :

1) Factoriser E = 4x²-49=(2x+7)(2x-7)

2) Soit l’expression F= (2x-7)(-5x+9)+4x²-49 .

a) développer puis réduire F.

F= -10x² + 18x + 35x – 63 + 4x²- 49

F = – 6x²+53x-112

b)calculer la valeur exacte de F lorsque $x=1$ , $x=-\frac{1}{2}$ , $x=\sqrt{2}$ .

$F = - 6\times1^2+53\times1-112=-6+53-112=-65$

$F = - 6\times\left (-\frac{1}{2} \right )^2+53\times\left (-\frac{1}{2} \right )-112=-\frac{6}{4}-\frac{106}{4}-\frac{448}{4}=\frac{336}{4}=84$

$F = - 6\times\left (\sqrt{2} \right )^2+53\times\left (\sqrt{2}\right )-112=-6\times2+53\times 2-112=-12+106-112=-18$

c)écrire F sous forme d’un produit de facteurs du premier degré .

$F = (2x-7)(-5x+9)+E\\F=(2x-7)(-5x+9)+(2x-7)(2x+7)$

$F = (2x-7)(-5x+9+2x+7)$

${\color{DarkRed} F = (2x-7)(-3x+16)}$

d)Résoudre l’équation F=0 .

$(2x-7)(-3x+16)=0$

Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul .

$(2x-7)=0\,\,ou\,\,(-3x+16)=0$

$2x=7\,\,ou\,\,-3x=-16$

$x=\frac{7}{2}\,\,ou\,\,x=\frac{-16}{-3}$

$x=3,5\,\,ou\,\,x=\frac{16}{3}$

Exercice 21 :

On donne l’expression A= (2x-3)²-(4x+7)(2x-3) .

1. Développer et réduire A.

$A=4x^2-12x+9-(8x^2-12x+14x-21)$

$A=4x^2-12x+9-8x^2+12x-14x+21$

$A=-4x^2-14x+30$

2. Factoriser A .

$A=(2x-3)((2x-3)-(4x+7))$

$A=(2x-3)(2x-3-4x-7)$

$A=(2x-3)(-2x-10)$

3. Résoudre l’équation (2x-3)(-2x-10)= 0

$2x-3=0\,ou\,-2x-10=0$

$x=\frac{3}{2}\,ou\,x=\frac{10}{2}$

$x=\frac{3}{2}\,ou\,x=5$

Exercice 22 :

Un boulanger vend les deux tiers de ses baguettes le matin.

L’après-midi, il en vend encore 90.

Le soir, il lui reste 20 baguettes.

Combien avait-il cuit de baguettes pour la journée ?

Notons x: le nombre de baguettes préparées pour la journée.

$\frac{2}{3}x+90=x-20$

$\frac{2}{3}x-x=-90-20$

$\frac{2}{3}x-\frac{3}{3}x=-110$

$-\frac{1}{3}x=-110$

$x=\frac{-110}{-\frac{1}{3}}$

$x=-110\times (-3)$

${\color{DarkRed} x=330}$

Il a préparé 330 baguettes.

Exercice 23 :

Les deux questions suivantes sont liées .

1) Développez $(3x-5)(x+3)$ .

$3x\times x+3x\times 3-5\times x-5\times 3$

$3x^2+9x-5 x-15$

${\color{DarkRed} 3x^2+4x-15}$

2) Résolvez l’équation $3x^2+4x-15=0$ .

$(3x-5)(x+3)=0$

Propriété :

Un produit de facteurs est nul si et seulement un des facteurs, au moins est nul.

$3x-5=0\,\,et\,\,x+3=0$

${\color{DarkRed} x=\frac{5}{3}\,\,et\,\,x=-3}$

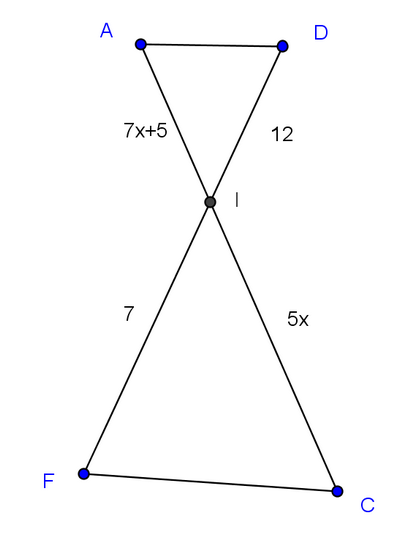
Exercice 24 :

Les droites (FC) et (DA) sont parallèles si $\frac{IA}{IC}=\frac{ID}{IF}$ .

$\frac{7x+5}{5x}=\frac{12}{7}$

$7(7x+5)=12\times 5x$

$49x+35=60x$

$60x-49x=35$

$11x=35$

$x=\frac{35}{11}$

Les équations et problèmes : corrigé des exercices en 3ème.

Les équations et problèmes : corrigé des exercices de maths en 3ème en PDF.

Volumes et sections : corrigé des exercices de maths en 3ème en PDF.

Fonctions linéaires : corrigé des exercices de maths en 3ème en PDF.

Les fonctions affines : corrigé des exercices de maths en 3ème en PDF.

Notez Mathovore !