Raisonnement par récurrence : corrigé des exercices en terminale.

🔍Corrigés Détaillés

Terminale • Lycée

Raisonnement par récurrence

🔎 Analyse : 16 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths sur le raisonnement par récurrence et la démonstration en utilisant le principe de récurrence en terminale.

Exercice 1 :
Soit 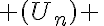$(U_n) \,$ la suite définie par

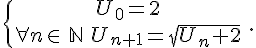
$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,\,U_{n+1}=\sqrt{U_n+2}} \,.$

Démontrer par récurrence que :

$\fbox{\forall n \in\,\mathbb{N}\,,\,U_n\le2 }\,$

soit la propriété de récurrence : 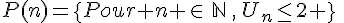$P(n)=\{Pour n \in\,\mathbb{N}\,,\,U_n\le2 \}\,$

Initialisation : P(0)

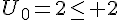$U_0=2\le 2$ donc P(0) vraie.

Supposons qu’il existe 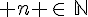$n \in\,\mathbb{N}$ tel que P(n) soit vraie, Montrons P(n+1) reste vraie.

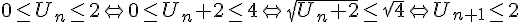
$0\le U_n\le 2\Leftrightarrow 0\le U_n+2\le 4 \Leftrightarrow \sqrt{U_n+2}\le \sqrt{4}\Leftrightarrow U_{n+1}\le 2$

donc P(n+1) reste vraie

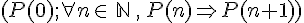
$(P(0); \forall n \in\,\mathbb{N}\,,\,P(n)\Rightarrow P(n+1))$

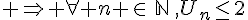
$\Rightarrow \forall n \in\,\mathbb{N}\,,U_n\le2$

Exercice 2 :

Soit 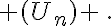$(U_n) \,.$ la suite définie par

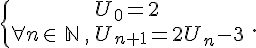
$\{{U_0=2\atop \forall n \in\,\mathbb{N}\,,\,U_{n+1}=2U_n-3} \,.$

Démontrer par récurrence que :

$\fbox{\forall n \in\,\mathbb{N}\,,\,U_n=3-2^n }\,.$

soit la propri&eacute:té de récurrence :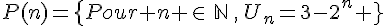 $P(n)=\{Pour n \in\,\mathbb{N}\,,\,U_n=3-2^n }\,$

Initialisation : P(0)

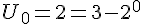$U_0=2=3-2^0$ donc P(0) vraie.

Supposons qu’il existe 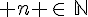$n \in\,\mathbb{N}$ tel que P(n) soit vraie, Montrons P(n+1) reste vraie.

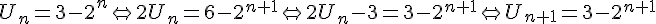
$U_n=3-2^n\Leftrightarrow 2U_n=6-2^{n+1} \Leftrightarrow 2U_n-3=3-2^{n+1} \Leftrightarrow U_{n+1}=3-2^{n+1}$

donc P(n+1) reste vraie

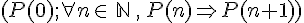
$(P(0); \forall n \in\,\mathbb{N}\,,\,P(n)\Rightarrow P(n+1))$

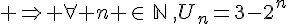
$\Rightarrow \forall n \in\,\mathbb{N}\,,U_n=3-2^n$

Exercice 3 :

On pose :

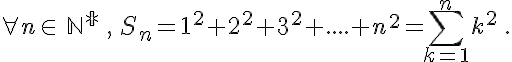
$\forall n \in\,\mathbb{N^*}\,,\,S_n=1^2+2^2+3^2+....+n^2=\sum_{k=1}^n k^2 \,.$

a. Calculer 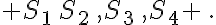$S_1\,S_2\,,S_3\,,S_4 \,.$

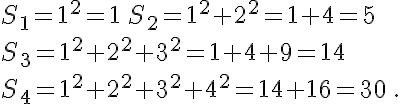
$S_1=1^2=1\,S_2=1^2+2^2=1+4=5\S_3=1^2+2^2+3^2=1+4+9=14\S_4=1^2+2^2+3^2+4^2=14+16=30 \,.$

b. Exprimer $S_{n+1}$ en fonction de $S_n$ .

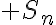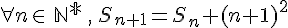
$\forall n \in\,\mathbb{N^*}\,,\, S_{n+1}=S_n+(n+1)^2$

c. Démontrer par récurrence que :

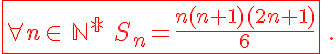
$\fbox{ \forall n \in\,\mathbb{N^*}\,\,S_n=\frac{n(n+1)(2n+1)}{6} }\,.$

soit la propri&eacute:té de récurrence :

$P(n)=\{Pour n \in\,\mathbb{N^*}\,,\,S_n=\frac{n(n+1)(2n+1)}{6} }\,$

Initialisation : P(1)

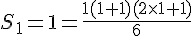$S_1=1=\frac{1(1+1)(2\times 1+1)}{6}$ donc P(1) vraie.

Supposons qu’il existe 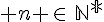$n \in\,\mathbb{N^*}$ tel que P(n) soit vraie, Montrons P(n+1) reste vraie.

$S_{n+1}=S_n+(n+1)^2\Leftrightarrow S_{n+1}=\frac{n(n+1)(2n+1)}{6}+(n+1)^2 \\Leftrightarrow S_{n+1}=\frac{n(n+1)(2n+1)+6(n+1)^2}{6} \\Leftrightarrow S_{n+1}=\frac{(n+1)[n(2n+1)+6(n+1)]}{6}$

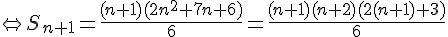
$\Leftrightarrow S_{n+1}=\frac{(n+1)(2n^2+7n+6)}{6}=\frac{(n+1)(n+2)(2(n+1)+3)}{6}$

donc P(n+1) reste vraie

$(P(0); \forall n \in\,\mathbb{N^*}\,,\,P(n)\Rightarrow P(n+1))$

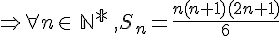
$\Rightarrow \forall n \in\,\mathbb{N^*}\,,S_n=\frac{n(n+1)(2n+1)}{6}$

Exercice 4 :

1. Le résultat est vrai pour n = 1 car :

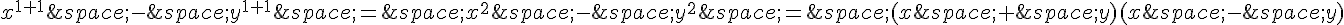
$x^{1+1}\,-\,y^{1+1}\,=\,x^2\,-\,y^2\,=\,(x\,+\,y)(x\,-\,y)$

Et on sait que 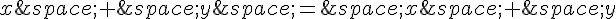$x\,+\,y\,=\,x\,+\,y$ et $x\,-\,y\,=\,x\,-\,y$ .

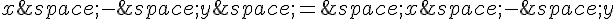Supposons maintenant que le résultat soit vrai pour un certain entier naturel n. On a :

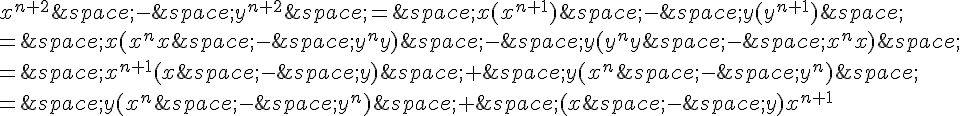$x^{n+2}\,-\,y^{n+2}\,=\,x(x^{n+1})\,-\,y(y^{n+1})\,\=\,x(x^{n}x\,-\,y^{n}y)\,-\,y(y^{n}y\,-\,x^{n}x)\,\=\,x^{n+1}(x\,-\,y)\,+\,y(x^{n}\,-\,y^{n})\,\=\,y(x^{n}\,-\,y^{n})\,+\,(x\,-\,y)x^{n+1}$ par la formule obtenue pour n=1

Donc, le résultat est bien vrai pour tout entier naturel n.

2. Quand k = n, on a :

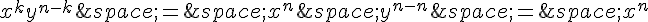
$x^ky^{n-k}\,=\,x^n\,y^{n-n}\,=\,x^n$

3. L’hypothèse est vraie pour n = 1 car :

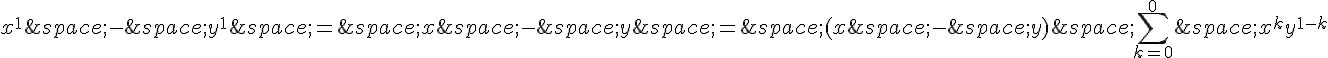
$x^1\,-\,y^1\,=\,x\,-\,y\,=\,(x\,-\,y)\,\sum_{k=0}^{0}\,x^ky^{1-k}$

Supposons maintenant que le résultat soit vrai pour un certain entier naturel n. On a :

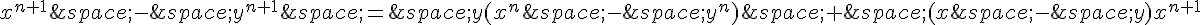$x^{n+1}\,-\,y^{n+1}\,=\,y(x^n\,-\,y^n)\,+\,(x\,-\,y)x^{n+1}$ par la formule obtenue pour la question 1,
et donc :

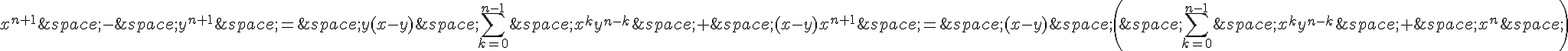
$x^{n+1}\,-\,y^{n+1}\,=\,y(x-y)\,\sum_{k=0}^{n-1}\,x^ky^{n-k}\,+\,(x-y)x^{n+1}\,=\,(x-y)\,(\,\sum_{k=0}^{n-1}\,x^ky^{n-k}\,+\,x^{n}\,)$

Donc, le résultat est vrai pour tout entier naturel n.

Exercice 5 :

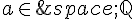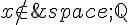1. Soient a et x deux nombres tels que $a\in\,\mathbb{Q}$ et $x\notin\,\mathbb{Q}$ .

On suppose par l’absurde que 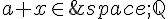$a+x\in\,\mathbb{Q}$ .

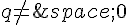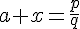Alors il existe deux entiers relatifs p et q avec $q\neq\,0$ tels que $a+x=\frac{p}{q}$ .

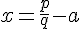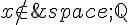On peut réarranger cette équation pour obtenir $x=\frac{p}{q}-a$ , qui est donc un nombre rationnel puisque p, q et a sont des nombres rationnels, ce qui contredit l’hypothèse que $x\notin\,\mathbb{Q}$ .

Donc, 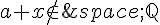$a+x\notin\,\mathbb{Q}$ .

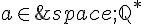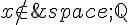2. Soient a et x deux nombres tels que $a\in\,\mathbb{Q}^*$ et $x\notin\,\mathbb{Q}$ .

On suppose par l’absurde que 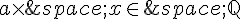$a\times \,x\in\,\mathbb{Q}$ .

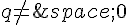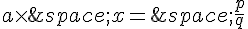Alors il existe deux entiers relatifs p et q avec $q\neq\,0$ tels que $a\times \,x=\,\frac{p}{q}$ .

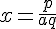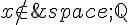On peut réarranger cette équation pour obtenir $x=\frac{p}{aq}$ , qui est donc un nombre rationnel puisque p, q et a sont des nombres rationnels, ce qui contredit l’hypothèse que $x\notin\,\mathbb{Q}$ .

Donc, 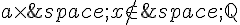$a\times \,x\notin\,\mathbb{Q}$ .

Exercice 6 :

Pour n = 0, on a :

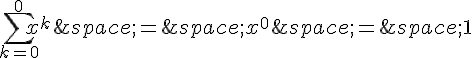
$\sum_{k=0}^{0}x^k\,=\,x^0\,=\,1$

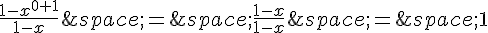
$\frac{1-x^{0+1}}{1-x}\,=\,\frac{1-x}{1-x}\,=\,1$

Donc la formule est vraie pour n = 0.

Supposons maintenant que la formule soit vraie pour un certain entier naturel n quelconque. Nous allons démontrer qu’elle est vraie pour n+1. On a :

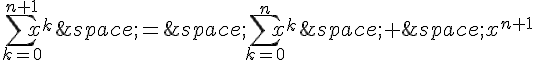
$\sum_{k=0}^{n+1}x^k\,=\,\sum_{k=0}^{n}x^k\,+\,x^{n+1}$

Par hypothèse de récurrence, on a :

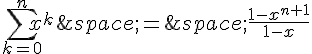
$\sum_{k=0}^{n}x^k\,=\,\frac{1-x^{n+1}}{1-x}$

Ainsi,

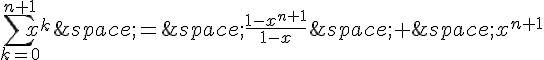
$\sum_{k=0}^{n+1}x^k\,=\,\frac{1-x^{n+1}}{1-x}\,+\,x^{n+1}$

En factorisant par (1-x), on a :

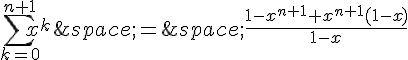
$\sum_{k=0}^{n+1}x^k\,=\,\frac{1-x^{n+1}+x^{n+1}(1-x)}{1-x}$

Et donc :

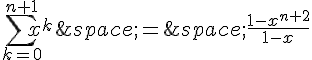
$\sum_{k=0}^{n+1}x^k\,=\,\frac{1-x^{n+2}}{1-x}$

Donc la formule est vraie pour tout entier naturel n.

Exercice 7 :

Pour n = 1, on a :

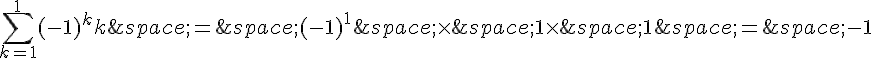
$\sum_{k=1}^{1}(-1)^kk\,=\,(-1)^1\,\times \,1\times \,1\,=\,-1$

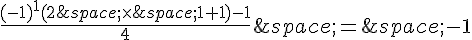
$\frac{(-1)^1(2\,\times \,1+1)-1}{4}\,=\,-1$

La formule est donc vraie pour n = 1.

Supposons maintenant que la formule soit vraie pour un certain entier naturel n quelconque. Nous allons démontrer qu’elle est vraie pour n+1. On a :

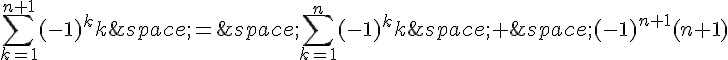
$\sum_{k=1}^{n+1}(-1)^kk\,=\,\sum_{k=1}^{n}(-1)^kk\,+\,(-1)^{n+1}(n+1)$

Par hypothèse de récurrence, on a :

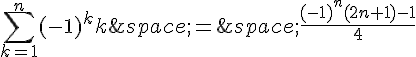
$\sum_{k=1}^{n}(-1)^kk\,=\,\frac{(-1)^n(2n+1)-1}{4}$

Donc,

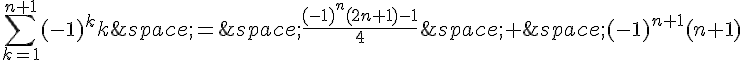
$\sum_{k=1}^{n+1}(-1)^kk\,=\,\frac{(-1)^n(2n+1)-1}{4}\,+\,(-1)^{n+1}(n+1)$

En factorisant par 4, on a :

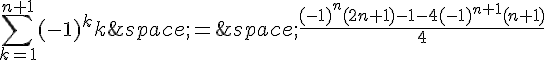
$\sum_{k=1}^{n+1}(-1)^kk\,=\,\frac{(-1)^n(2n+1)-1-4(-1)^{n+1}(n+1)}{4}$

En simplifiant, on obtient :

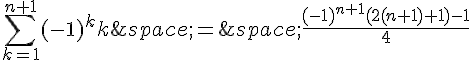
$\sum_{k=1}^{n+1}(-1)^kk\,=\,\frac{(-1)^{n+1}(2(n+1)+1)-1}{4}$

Donc la formule est vraie pour tout entier naturel n.

Exercice 8 :

Pour n = 0, on a :

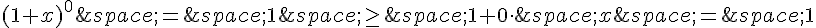
$(1+x)^0\,=\,1\,\geq\,\,1+0\times \,\,x\,=\,1$

Donc la formule est vraie pour n = 0.

Supposons maintenant que la formule soit vraie pour un certain entier naturel n quelconque. Nous allons démontrer qu’elle est vraie pour n+1.

On a :

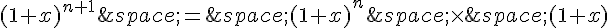
$(1+x)^{n+1}\,=\,(1+x)^n\,\times \,(1+x)$

Par hypothèse de récurrence, on a :

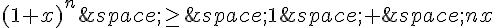
$(1+x)^n\,\geq\,\,1\,+\,nx$

Donc,

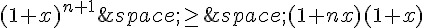
$(1+x)^{n+1}\,\geq\,\,(1+nx)(1+x)$

En développant le membre de droite, on obtient :

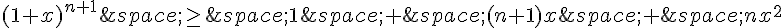
$(1+x)^{n+1}\,\geq\,\,1\,+\,(n+1)x\,+\,nx^2$

Comme x est positif, 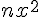$nx^2$ est positif ou nul. On peut donc écrire :

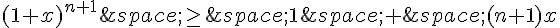
$(1+x)^{n+1}\,\geq\,\,1\,+\,(n+1)x$

La formule est donc vraie pour tout entier naturel n.

Remarque : cette inégalité est appelée inégalité de Bernoulli.

Exercice 9 :

1. La contraposée de la proposition précédente est :

Si l’entier n est impair, alors 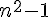$n^2-1$ est divisible par 8.

2. Supposons que n soit impair, c’est-à-dire n = 2k+1 pour un certain entier naturel k.

Alors :

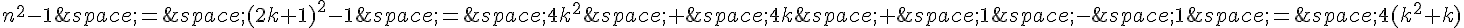
$n^2-1\,=\,(2k+1)^2-1\,=\,4k^2\,+\,4k\,+\,1\,-\,1\,=\,4(k^2+k)$

Donc 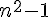$n^2-1$ est divisible par 4.

Pour montrer qu’il est divisible par 8, il suffit de remarquer que 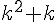$k^2+k$ est pair pour tout entier k.

En effet, pour k pair, on a 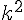$k^2$ pair et k pair donc 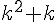$k^2+k$ pair.

Pour k impair, on a 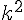$k^2$ impair et k impair donc 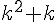$k^2+k$ pair.

Donc 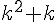$k^2+k$ est pair dans tous les cas et n^2-1 est divisible par 8.

Donc la contraposée est vraie.

3. On peut en déduire que si 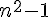$n^2-1$ n’est pas divisible par 8, alors n est pair.

En effet, si n était impair, alors d’après la contraposée, 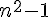$n^2-1$ serait divisible par 8, ce qui est contraire à l’hypothèse de départ.

Donc si 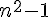$n^2-1$ n’est pas divisible par 8, alors n est pair.

Exercice 10 :

1. Nous allons utiliser une démonstration par récurrence.

Vérifions la propriété pour n = 1 :

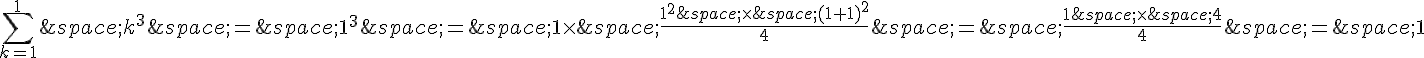
$\sum_{k=1}^{1}\,k^3\,=\,1^3\,=\,1\times \,\frac{1^2\,\times \,(1+1)^2}{4}\,=\,\frac{1\,\times \,4}{4}\,=\,1$

La propriété est vérifiée au rang 1.

Supposons maintenant que la propriété soit vraie pour un certain entier naturel k, c’est-à-dire :

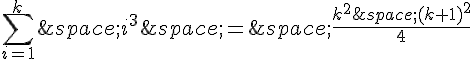
$\sum_{i=1}^{k}\,i^3\,=\,\frac{k^2\,(k+1)^2}{4}$

Prouvons que la propriété est vraie pour k+1 :

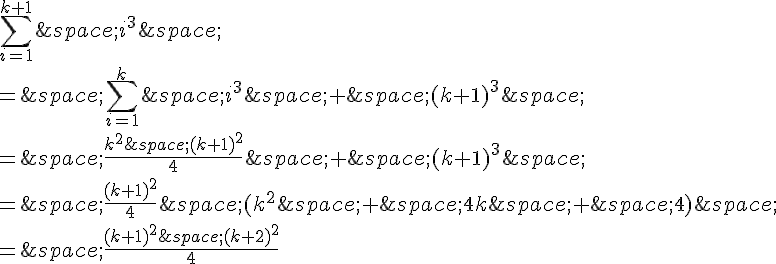
$\sum_{i=1}^{k+1}\,i^3\,\=\,\sum_{i=1}^{k}\,i^3\,+\,(k+1)^3\,\=\,\frac{k^2\,(k+1)^2}{4}\,+\,(k+1)^3\,\=\,\frac{(k+1)^2}{4}\,(k^2\,+\,4k\,+\,4)\,\=\,\frac{(k+1)^2\,(k+2)^2}{4}$

Donc la propriété est vraie pour tout entier naturel n.

2. En utilisant la formule obtenue à la question 1, on peut calculer :

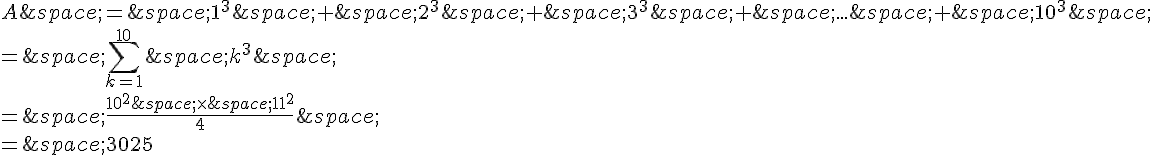
$A\,=\,1^3\,+\,2^3\,+\,3^3\,+\,...\,+\,10^3\,\=\,\sum_{k=1}^{10}\,k^3\,\=\,\frac{10^2\,\times \,11^2}{4}\,\=\,3025$

Donc A vaut 3025.

Multiples :

Pour tout entier n, on a :

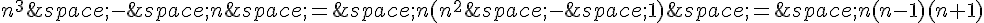
$n^3\,-\,n\,=\,n(n^2\,-\,1)\,=\,n(n-1)(n+1)$

Un produit de trois entiers consécutifs est toujours divisible par 3, car il contient un multiple de 3.

Par conséquent, 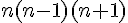$n(n-1)(n+1)$ est toujours divisible par 3, et donc 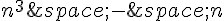$n^3\,-\,n$ est un multiple de 3 pour tout entier n.

Exercice 11 :

1. Nous allons utiliser la formule du binôme de Newton pour développer 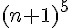$(n+1)^5$ :

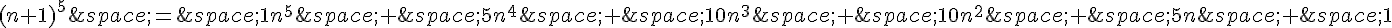
$(n+1)^5\,=\,1n^5\,+\,5n^4\,+\,10n^3\,+\,10n^2\,+\,5n\,+\,1$

On peut ordonner les termes en partant du terme de plus haut degré (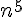 $n^5$ ) et en descendant jusqu’au terme constant (1), ce qui donne :

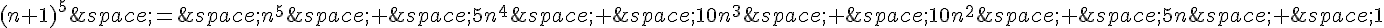
$(n+1)^5\,=\,n^5\,+\,5n^4\,+\,10n^3\,+\,10n^2\,+\,5n\,+\,1$

2. Posons m = n+1. Alors on a :

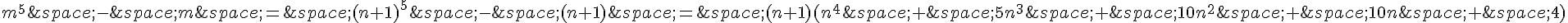
$m^5\,-\,m\,=\,(n+1)^5\,-\,(n+1)\,=\,(n+1)(n^4\,+\,5n^3\,+\,10n^2\,+\,10n\,+\,4)$

Nous allons montrer que 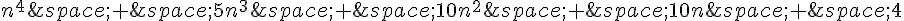$n^4\,+\,5n^3\,+\,10n^2\,+\,10n\,+\,4$ est un multiple de 5 pour tout entier n.

Remarquons que si n est divisible par 5, alors 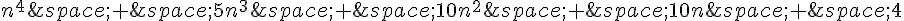$n^4\,+\,5n^3\,+\,10n^2\,+\,10n\,+\,4$ est clairement un multiple de 5 (car le dernier chiffre de 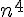$n^4$ est 1).

Sinon, n n’est pas divisible par 5, donc son reste dans la division par 5 est 1, 2, 3 ou 4.

Nous allons distinguer ces 4 cas :

– Si n a pour reste 1 dans la division par 5, alors 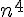$n^4$ a pour reste 1 dans la division par 5, et de même pour 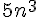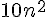$5n^3$ , $10n^2$ et 10n.

Donc 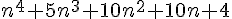$n^4+5n^3+10n^2+10n+4$ a pour reste 0 dans la division par 5.
– Si n a pour reste 2 dans la division par 5, alors 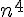$n^4$ a pour reste 1 dans la division par 5, et de même pour 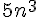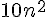$5n^3$ , $10n^2$ et 10n.

Donc 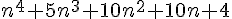$n^4+5n^3+10n^2+10n+4$ a pour reste 0 dans la division par 5.
– Si n a pour reste 3 dans la division par 5, alors n^4 a pour reste 1 dans la division par 5, et de même pour 5n^3 et 10n.

On remarque que 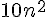$10n^2$ a pour reste 0 dans la division par 5 car il se termine par 00, et que 4 a pour reste -1 dans la division par 5.

Donc 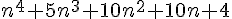$n^4+5n^3+10n^2+10n+4$ a pour reste 0 dans la division par 5.
– Si n a pour reste 4 dans la division par 5, alors 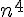$n^4$ a pour reste 1 dans la division par 5, et de même pour 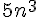$5n^3$ et 10n.

On remarque que 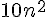$10n^2$ a pour reste 0 dans la division par 5 car il se termine par 00, et que 4 a pour reste -1 dans la division par 5.

Donc 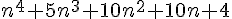$n^4+5n^3+10n^2+10n+4$ a pour reste 0 dans la division par 5.

Dans tous les cas, 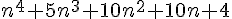$n^4+5n^3+10n^2+10n+4$ est un multiple de 5.

Donc 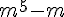$m^5-m$ est divisible par 5 pour tout entier m, et donc 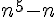$n^5-n$ est un multiple de 5 pour tout entier n.

Exercice 12 :

Nous allons procéder par récurrence.

Vérifions la propriété pour n = 1 :

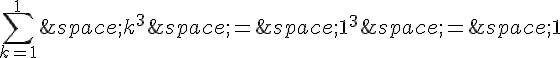
$\sum_{k=1}^{1}\,k^3\,=\,1^3\,=\,1$
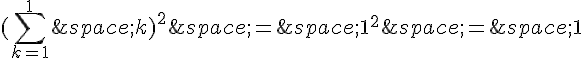
$(\sum_{k=1}^{1}\,k)^2\,=\,1^2\,=\,1$

La propriété est vérifiée au rang 1.

Supposons maintenant que la propriété soit vraie pour un certain entier naturel k, c’est-à-dire :

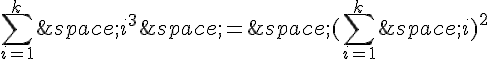
$\sum_{i=1}^{k}\,i^3\,=\,(\sum_{i=1}^{k}\,i)^2$

Prouvons que la propriété est vraie pour k+1 :

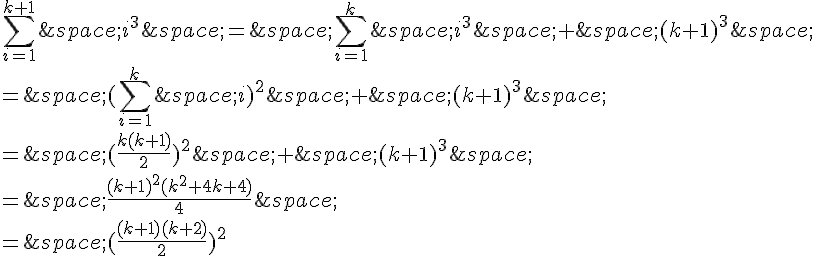
$\sum_{i=1}^{k+1}\,i^3\,=\,\sum_{i=1}^{k}\,i^3\,+\,(k+1)^3\,\\=\,(\sum_{i=1}^{k}\,i)^2\,+\,(k+1)^3\,\\=\,(\frac{k(k+1)}{2})^2\,+\,(k+1)^3\,\\=\,\frac{(k+1)^2(k^2+4k+4)}{4}\,\\=\,(\frac{(k+1)(k+2)}{2})^2$

Donc la propriété est vraie pour tout entier naturel n.

4.9/5 - (36827 votes)

Raisonnement par récurrence : corrigé des exercices en terminale.

Raisonnement par récurrence : corrigé des exercices de maths en terminale en PDF.

Probabilités : corrigé des exercices de maths en 1ère.

Barycentre : corrigé des exercices de maths en terminale en PDF.

Calcul intégral : corrigé des exercices de maths en terminale en PDF.

Notez Mathovore !