Le cercle : corrigé des exercices de maths en 6ème en PDF.

Mon application

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

🔍Corrigés Détaillés

6eme • Scolaire

Le cercle et constructions

🔎 Analyse : 15 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices sur le cercle en 6ème avec des problème sur la construction de cercles et le tracé de corde en sixième.

Exercice 1 :

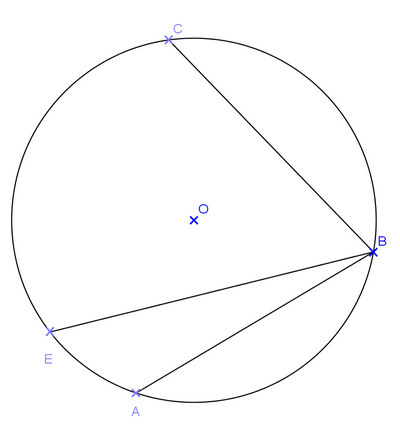
1. Tracer un cercle de centre O et une corde [AB] comme ci-dessous.

2. Tracer une corde [BC] de façon que le point O soit à l’intérieur du triangle ABC.

3. Tracer une corde [BE] de façon que le point O soit à l’extérieur du triangle ABE.

Exercice 2 :

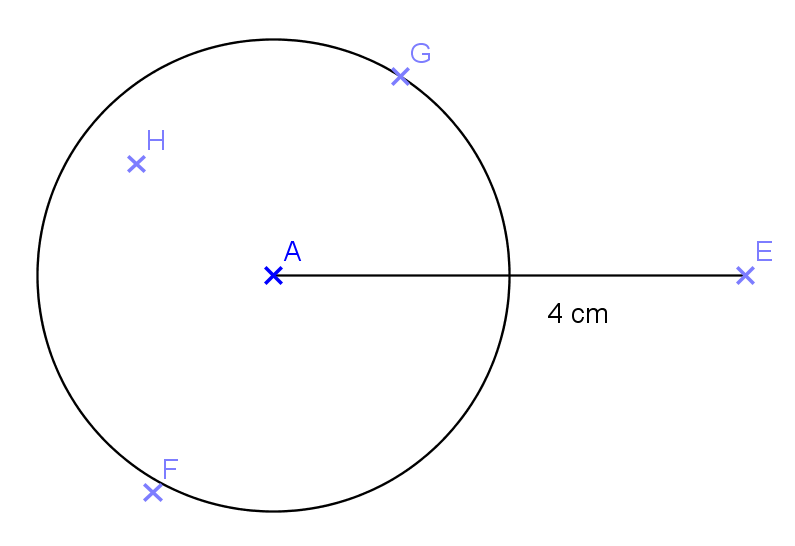
1.2. Voici la figure que nous obtenons :

3. Indiquer pour chaque point A,E,F,G,H s’il appartient ou non au cercle $\varphi$ .

Uniquement le point G appartient au cercle car AG=2 cm = rayon

Exercice 3 :

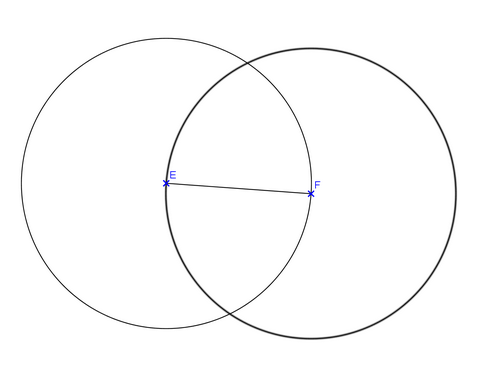
1. Tracer un segment [EF], puis le cercle de centre E passant par F.

2. Tracer le cercle de centre F et de rayon EF.

Deux cercles

Exercice 4 :

1. Tracer un segment [PQ] et placer son milieu H.

2. Tracer le cercle de centre H passant par P.

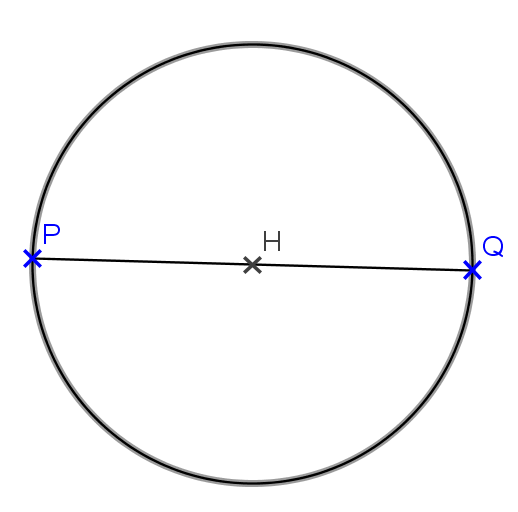
Cercle et diamètre

Citer un segment qui est un diamètre de ce cercle.

Le segment [PQ] est un diamètre de ce cercle .

Exercice 5 :

1. Placer sur la feuille deux points A et B distants de 4 cm.

2. Tracer le cercle de centre A passant par B.

Quel est son rayon ? son diamètre ?

Son rayon est de 4 cm et son diamètre est de 8 cm.

Exercice 6 :

1. Placer un point O sur la feuille.

Tracer le cercle de centre O et de rayon 3 cm.

2. Tracer le cercle de centre O et de diamètre 5 cm.

Exercice 7 :

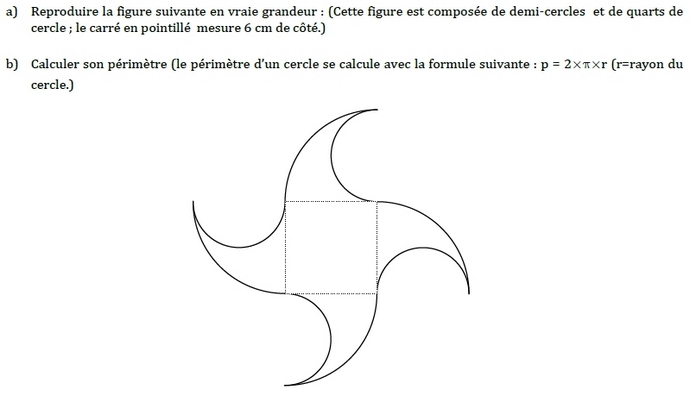
Exercice 8 :

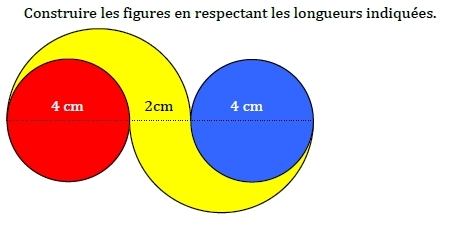
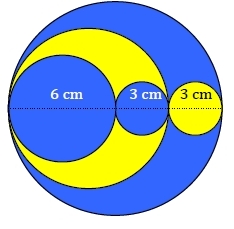
b) Cette figure correspond à 2 petits cercles de rayon 3 cm et un grand cercle de rayon 6 cm .

$P=2\times 2\times \pi\times 3+2\times \pi\times 6$

$P=12\pi+12 \pi$

$P=24\pi$

$P\simeq 75,4\,cm$

Exercice 9 :

Cercles

Exercice 21 :

Exercice 22 :

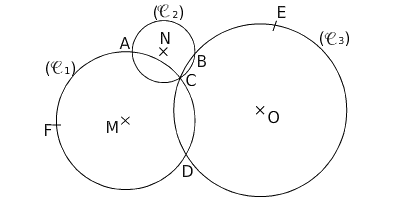
Les trois points M, N et O sont les centres respectifs des cercles $(C_1);(C_2);(C_3)$ .

Les affirmations suivantes sont-elles vraies ou fausses ?

[AC] est un diamètre du cercle $(C_2)$ : faux.
A et C sont les points d’intersection des cercles $(C_1)$ et $(C_2)$ : vrai.
[CD] est une corde de deux cercles : vrai.
EO =OD : vrai.
MC est le rayon du cercle $(C_1)$ : vrai.
Le cercle $(C_2)$ passe par les points A, B et C : vrai.

Exercice 23 :

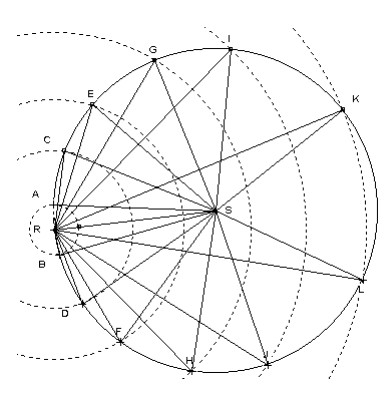
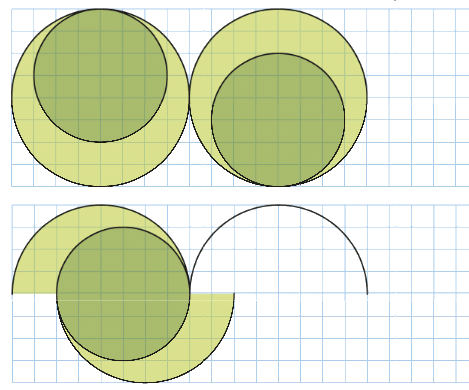
Poursuivre chacune des frises ci-dessous, en reproduisant le motif.

A vous de construire la suite…

Exercice 24 :

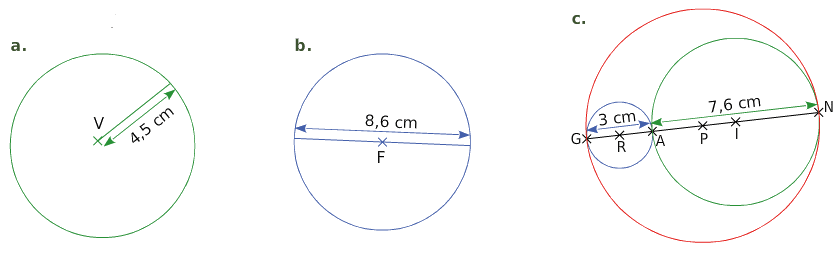
Ecrire un programme de construction pour chacune des figures suivantes :

a. Construire le cercle de centre V et de rayon 4,5 cm.

b. Construire le cercle de centre f et de diamètre 8,6 cm.

c. Construire le cercle de centre P et de rayon 5,3 cm.

Construire A milieu de [GP], construire R milieu de [AG].

Construire le cercle de diamètre [GA] et de centre R.

4.7/5 - (22250 votes)