Fonction exponentielle : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 18 septembre 2025
Exercice 1 :
Soit la fonction f définie par 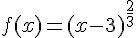
1. Donner le domaine de définition de la fonction f.
nous avons 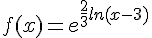
donc pour que f soit définie, il faut que x-3>0 soit x>3.
ainsi :
![{\color{DarkRed} D_f=]3;+\infty[}](https://mathovore.fr/latex-images/03535d40a7237305d6509a285521712a.png)
2. Donner une primitive de la fonction.
les primitives de f sont de la forme :
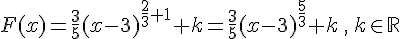
Exercice 2 :
soit la fonction f tel que : 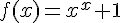
1. Indiquer le domaine de définition de f et transformer l’écriture du réel f(x).
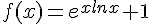
donc ![D_f=]0;+\infty[](https://mathovore.fr/latex-images/aced28fcb9330d31f9e50c9a61bae364.png)
2. Donner un prolongement par continuité de f au point 0.
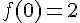
3. Etudier la dérivabilité de f au point 0.
4. Calculer la dérivée de f et étudier son signe. Etablir le tableau de variations.
5. Décrire comment se présente la tangente en ce point.
6. Construire la courbe dans un repère approprié.
Exercice 3 :
1. Démontrer que pour tout réel x, 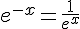 .
.
d’après la formule ci-dessus :
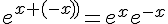
donc

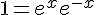
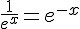 car
car 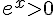
2. Démontrer que pour tout réel x et pour tout entier naturel n,
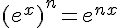
Exercice 4:
Résoudre les inéquations suivantes :
1. 
La fonction logarithme népérien est strictement croissante sur  .
.

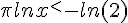
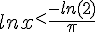
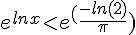
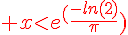
2. 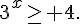
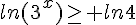
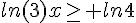
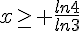 ( car ln 3 > 0)
( car ln 3 > 0)
Exercice 5 :
Déterminer les primitives des fonctions suivantes :
1. 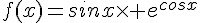 .
.
une primitive est de la forme 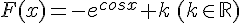 .
.
2. ![f(x)=x^{-2}e^{\frac{1}{x}}\,sur\,]-\infty;0[.](https://mathovore.fr/latex-images/327d6a80dd3a6acad6f2f528aba4954f.png)
une primitive est de la forme 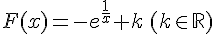 .
.
Exercice 6 :
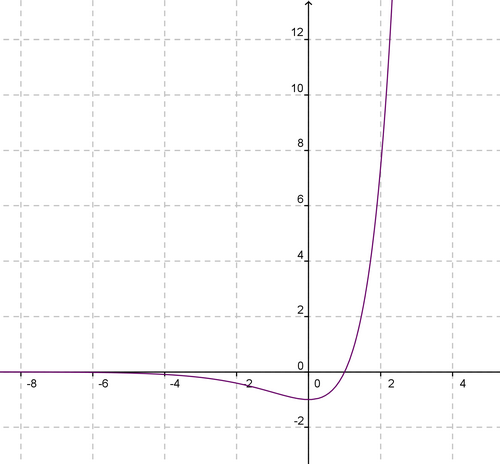
Soit 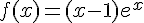 pour x ∈ R.
pour x ∈ R.
1. Déterminez les limites de f aux bornes du domaine de définition.
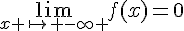 et
et 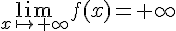
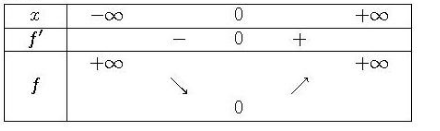
2. Etudiez les variations de f.
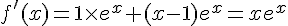
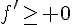 sur
sur 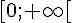 donc f est croissante sur
donc f est croissante sur 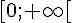 .
.
3. Construisez la courbe C représentant f.
Exercice 7 :
Résoudre les équations et inéquations proposées.
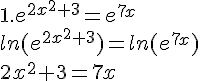

Calculons la valeur du discriminant :
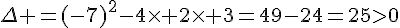
Le discriminant est strictement positif, il existe donc deux racines réelles distinctes.
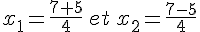
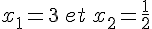
Exercice 8 :
1.a) Pour calculer la dérivée de 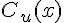 , on utilise la formule pour la dérivée d’un quotient :
, on utilise la formule pour la dérivée d’un quotient :
![C^{'}_{u(x)} = \frac{d}{dx}[x-10]+\frac{d}{dx}(\frac{900}{x}) = 1 - \frac{900}{x^2}](https://mathovore.fr/latex-images/3ef5daf3e4ae6b723ea8160b4e39c300.png)
En simplifiant, on obtient :
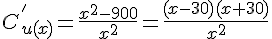
b) Le dénominateur est toujours positif car x est dans l’intervalle [10, 100].
Le numérateur est positif pour x > 30 et négatif pour x < 30.
Donc, le signe de 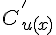 dépend du signe de (x-30)(x+30). On peut établir le tableau de signes suivant :
dépend du signe de (x-30)(x+30). On peut établir le tableau de signes suivant :
x | 10 | 30 | 100
—-|—–|—–|—–
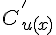 | – | 0 | +
| – | 0 | +
En utilisant ce tableau, on peut établir le tableau de variation de 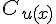 :
:
x | 10 | 30 | 100
—-|—–|—–|—–
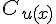 | + | mín | +
| + | mín | +
c) Le coût unitaire est le plus bas lorsque 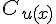 est minimal.
est minimal.
Comme la fonction 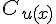 est décroissante sur [10,30] et croissante sur [30,100], son minimum est atteint en x = 30. Le coût unitaire minimal est donc
est décroissante sur [10,30] et croissante sur [30,100], son minimum est atteint en x = 30. Le coût unitaire minimal est donc 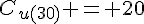 .
.
Le bénéfice de l’entreprise par objet vendu est la différence entre le prix de vente et le coût unitaire, soit :
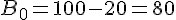
2. Le bénéfice global de l’entreprise est donné par la formule 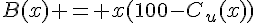 , car l’entreprise fabrique et vend x objets par jour.
, car l’entreprise fabrique et vend x objets par jour.
En remplaçant 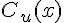 par son expression en fonction de x, on obtient :
par son expression en fonction de x, on obtient :
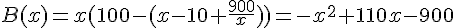
3. Pour trouver le maximum de la fonction B sur [10,100], on peut calculer sa dérivée :
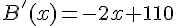
La dérivée est nulle en x = 55, ce qui est bien dans l’intervalle [10,100]. Pour déterminer que cette valeur est un maximum, on peut regarder le signe de la dérivée dans les intervalles [10,55] et [55,100]. On peut établir le tableau de signes suivant :
x | 10 | 55 | 100
—-|—–|—–|—–
B^'(x) | – | + | –
Donc, la fonction B est décroissante sur [10,55] et croissante sur [55,100], avec un maximum en x = 55. Le bénéfice maximal est donc 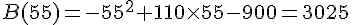 .
.
Exercice 9 :
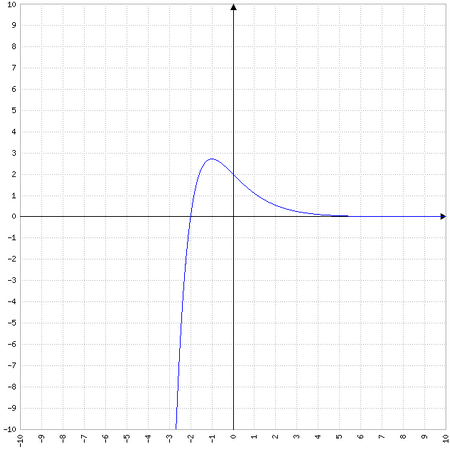
La courbe représente une fonction f définie par 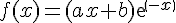 .
.
Elle passe par les points de coordonnées (o;2) et (-2;0).
1) Calculer a et b .
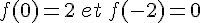

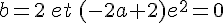
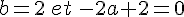

Conclusion : 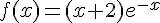
2) Déterminer les coordonnées du maximum après avoir étudié les variations de f.
f est dérivable sur  en tant que produit de fonctions dérivables sur cet intervalle .
en tant que produit de fonctions dérivables sur cet intervalle .
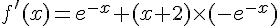
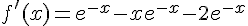

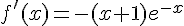
Le signe de f ‘ est celui de -x-1 puisque l’exponentielle est strictement positive sur R .
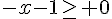
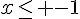
Conclusion : f est croissante sur ![]-\infty;-1]](https://mathovore.fr/latex-images/92c5730fc4afe15926037d88ab2b15b3.png) .
.
Exercice 10 :
Simplifier au maximum :
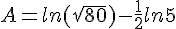
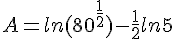
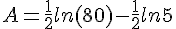
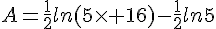
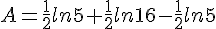

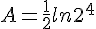
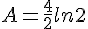
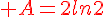
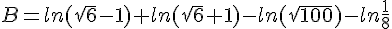
![B=ln[(\sqrt{6}-1)(\sqrt{6}+1)]-ln(100^{\frac{^1}{2}})-(-ln8) )](https://mathovore.fr/latex-images/d86f9e75bd2c48f39d29613508b10b0b.png)
![B=ln[(\sqrt{6})^2-1^2]-\frac{1}{2}ln(100)-(-ln8 )](https://mathovore.fr/latex-images/332df3585971df71d83454f66ae78e9d.png)
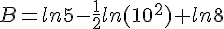
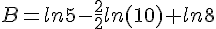
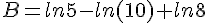
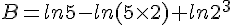
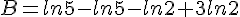

Exercice 11 :
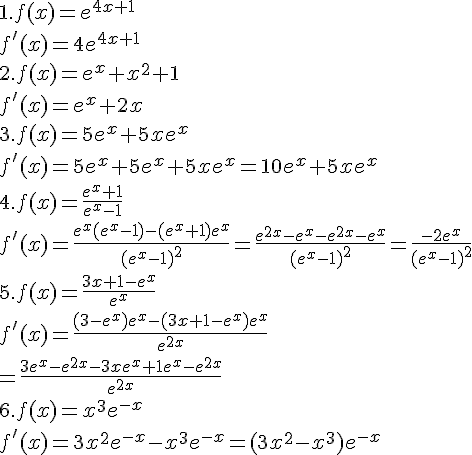
Exercice 12 :
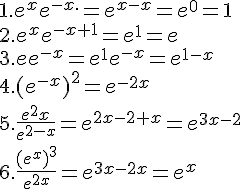
Exercice 13 :
1. On peut remarquer que l’équation peut être mise sous la forme d’une équation du second degré en 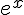 en posant
en posant 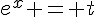 :
:
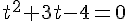
On peut résoudre cette équation en utilisant la méthode habituelle pour résoudre une équation quadratique :
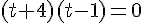
Donc, 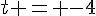 ou
ou 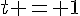 . En remplaçant par
. En remplaçant par 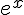 , on trouve que les solutions de l’équation sont :
, on trouve que les solutions de l’équation sont :
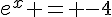 (pas de solution réelle) ou
(pas de solution réelle) ou 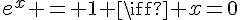
2. On factorise par 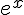 :
:

Donc, 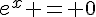 (pas de solution réelle) ou
(pas de solution réelle) ou 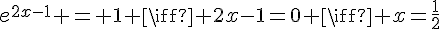
3. On peut remarquer que l’équation est similaire à 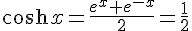 , qui est équivalente à
, qui est équivalente à 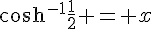 .
.
En utilisant la définition de la fonction cosinus hyperbolique inverse (aussi appelée arccosh), on a :

ou
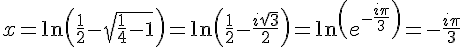
donc les solutions de l’équation sont 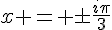 .
.
4. On peut diviser les deux membres de l’inéquation par 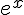 pour obtenir :
pour obtenir :
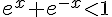
En utilisant la même astuce que précédemment, on remarque que cette inéquation équivaut à 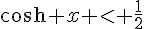 .
.
Or, on sait que 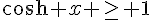 pour tout
pour tout 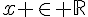 , donc il n’y a pas de solution à cette inéquation.
, donc il n’y a pas de solution à cette inéquation.
5. On peut réécrire l’inéquation sous la forme 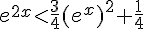 , ce qui peut être factorisé en
, ce qui peut être factorisé en 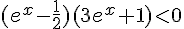 .
.
On peut résoudre cette inéquation en utilisant le tableau de signes suivant :
 |
| 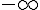 |
| 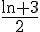 |
| 
— | — | — | —
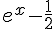 | | |
| | |
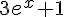 | | |
| | |
Produit | | |
Donc, les solutions sont 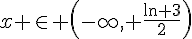 .
.
6. On peut appliquer la fonction exponentielle des deux côtés de l’inéquation, en prenant soin de conserver le sens de l’inégalité :
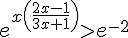
En utilisant la propriété de la fonction exponentielle 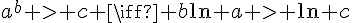 , on peut appliquer le logarithme naturel des deux côtés de l’inégalité :
, on peut appliquer le logarithme naturel des deux côtés de l’inégalité :
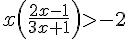
En multipliant par le dénominateur  (qui est toujours positif puisque
(qui est toujours positif puisque 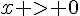 ), on obtient :
), on obtient :
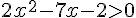
On peut résoudre cette inéquation en utilisant la méthode habituelle pour résoudre une inéquation quadratique :
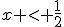 ou
ou 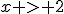
Mais on doit également vérifier que le dénominateur de la fraction initiale est toujours positif dans l’intervalle des solutions (c’est-à-dire 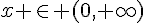 ),
),
sinon nous aurions une solution qui ne fonctionne pas.
Le dénominateur  est toujours positif dans cet intervalle, donc l’ensemble des solutions de l’inéquation initiale est
est toujours positif dans cet intervalle, donc l’ensemble des solutions de l’inéquation initiale est 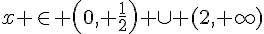 .
.
1. Pour tout 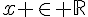 , on a :
, on a :
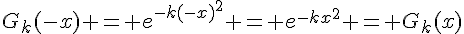
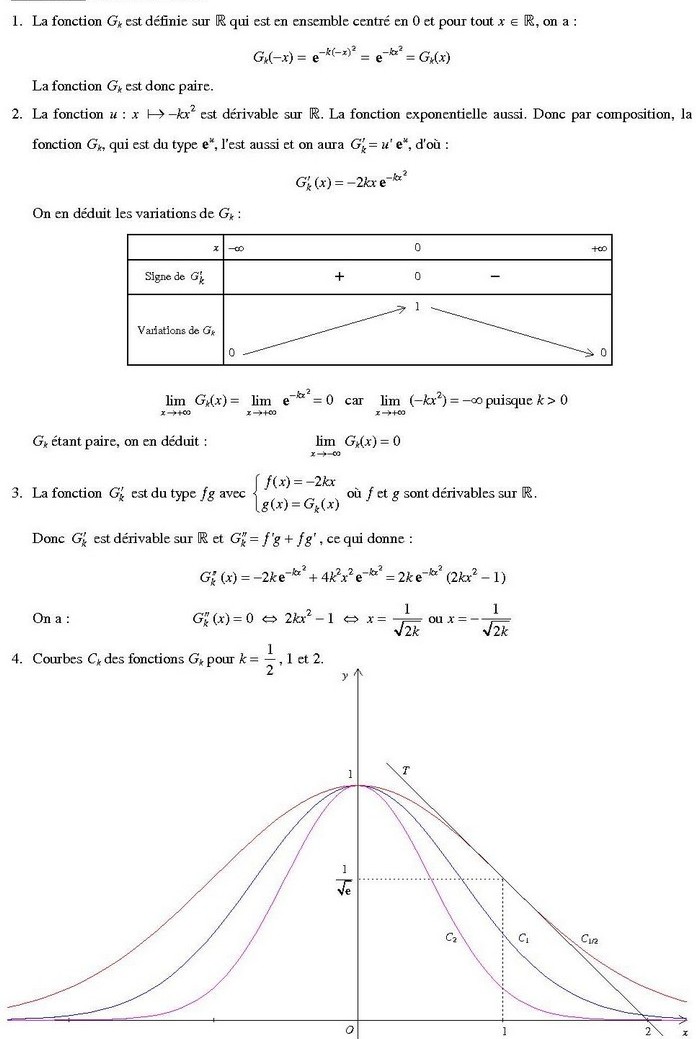
Donc, la fonction 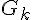 est paire.
est paire.
2. La fonction 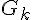 est bien dérivable sur
est bien dérivable sur  car elle est la composée de fonctions dérivables. Pour tout
car elle est la composée de fonctions dérivables. Pour tout 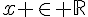 , on a :
, on a :
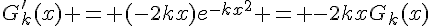
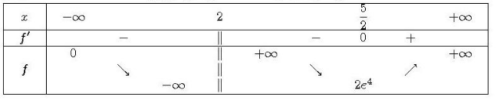
En utilisant le signe de 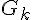 et le tableau de variations de
et le tableau de variations de 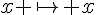 , on peut établir le tableau de variation de
, on peut établir le tableau de variation de 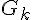 :
:
x |-\infty | 0 |\infty
———|————–|——–|——
G_k(x) |+\infty reste | 1 |+\infty reste
G’_k(x) | – | 0 |+
3. Pour résoudre 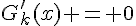 , on doit chercher les valeurs de
, on doit chercher les valeurs de  pour lesquelles
pour lesquelles 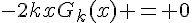 . Cette équation est vraie si et seulement si
. Cette équation est vraie si et seulement si 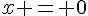 ou
ou 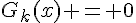 . La valeur
. La valeur 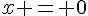 n’est pas une solution car ce point correspond à un maximum local de la fonction
n’est pas une solution car ce point correspond à un maximum local de la fonction 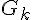 . Donc, les solutions doivent vérifier
. Donc, les solutions doivent vérifier 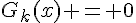 , c’est-à-dire
, c’est-à-dire 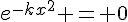 . Mais cette équation n’a pas de solution réelle car l’exponentielle est toujours strictement positive.
. Mais cette équation n’a pas de solution réelle car l’exponentielle est toujours strictement positive.
4. Voici les courbes de 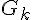 pour
pour 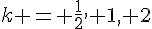 :
:

5. Pour tout 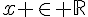 et pour tout
et pour tout 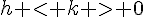 , on a :
, on a :
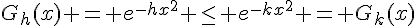
Cela s’explique par le fait que le coefficient 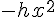 est plus petit (ou égal) que le coefficient
est plus petit (ou égal) que le coefficient 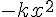 , donc l’exponentielle décroît moins rapidement pour
, donc l’exponentielle décroît moins rapidement pour  que pour
que pour 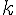 , ce qui fait que la fonction
, ce qui fait que la fonction 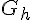 est plus grande (ou égale) que la fonction
est plus grande (ou égale) que la fonction 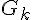 pour tout
pour tout 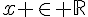 .
.
6. L’équation 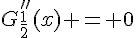 équivaut à
équivaut à 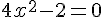 , qui a pour solution positive
, qui a pour solution positive 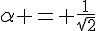 .
.
7. La tangente à la courbe de 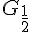 au point d’abscisse
au point d’abscisse  est la droite affine de coefficient directeur
est la droite affine de coefficient directeur 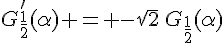 et passant par le point
et passant par le point 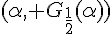 . On a donc :
. On a donc :

soit :
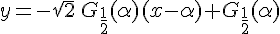
8. Voici le graphique de la fonction 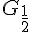 ainsi que de sa tangente en
ainsi que de sa tangente en 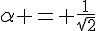 :
:
Exercice 16 :
Partie A
1a. Soit 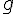 une fonction définie et dérivable sur
une fonction définie et dérivable sur  telle que
telle que 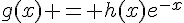 pour tout
pour tout 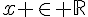 . En dérivant cette égalité par rapport à
. En dérivant cette égalité par rapport à  , on a :
, on a :
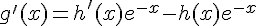
Pour que 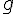 soit solution de l’équation différentielle
soit solution de l’équation différentielle 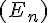 donnée, il faut que
donnée, il faut que 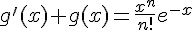 pour tout
pour tout 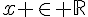 . En utilisant l’expression de
. En utilisant l’expression de 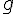 en fonction de
en fonction de  , on a :
, on a :
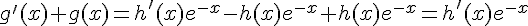
Donc 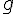 est solution de
est solution de 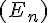 si et seulement si
si et seulement si  pour tout
pour tout 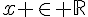 .
.
1b. En intégrant  par rapport à
par rapport à  , on obtient :
, on obtient :
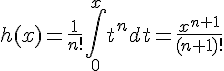
D’après la question précédente, la fonction 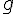 correspondante est donnée par :
correspondante est donnée par :

2a. Soit 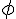 une fonction définie et dérivable sur
une fonction définie et dérivable sur  . Alors
. Alors 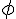 est solution de
est solution de 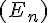 si et seulement si
si et seulement si 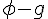 est solution de l’équation différentielle
est solution de l’équation différentielle 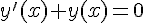 . En effet, en substituant
. En effet, en substituant 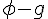 à
à  dans l’équation
dans l’équation 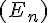 , on obtient :
, on obtient :
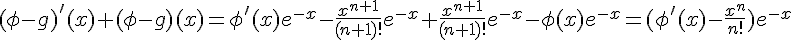
Pour que 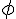 soit solution de
soit solution de 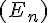 , il faut et il suffit que
, il faut et il suffit que 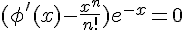 pour tout
pour tout 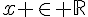 , c’est-à-dire que
, c’est-à-dire que 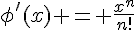 pour tout
pour tout 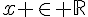 . On obtient ainsi que
. On obtient ainsi que 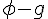 est solution de
est solution de 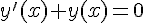 .
.
2b. L’équation 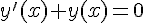 est une équation différentielle linéaire d’ordre 1 à coefficients constants. Sa solution générale est donnée par
est une équation différentielle linéaire d’ordre 1 à coefficients constants. Sa solution générale est donnée par 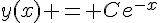 pour une constante
pour une constante 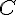 fixée en fonction des conditions initiales. Ici, on cherche à résoudre
fixée en fonction des conditions initiales. Ici, on cherche à résoudre 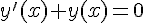 avec la condition initiale
avec la condition initiale 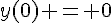 . En substituant
. En substituant 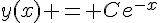 dans cette condition initiale, on obtient
dans cette condition initiale, on obtient  , donc la solution de cette équation avec cette condition initiale est
, donc la solution de cette équation avec cette condition initiale est  .
.
2c. Pour tout entier 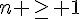 , notons
, notons 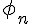 la solution de
la solution de 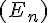 avec la condition initiale
avec la condition initiale 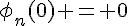 . On peut écrire :
. On peut écrire :

donc 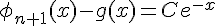 pour une certaine constante
pour une certaine constante 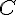 . En utilisant la condition initiale
. En utilisant la condition initiale 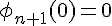 , on a
, on a 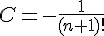 , donc :
, donc :
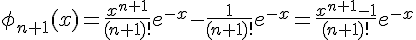
Ainsi, pour tout 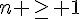 , la solution de
, la solution de 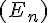 avec la condition initiale
avec la condition initiale 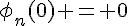 est donnée par :
est donnée par :
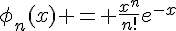
2d. En particulier, la solution de 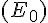 avec la condition initiale
avec la condition initiale 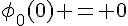 est donnée par
est donnée par  , donc d’après la question précédente, la solution de
, donc d’après la question précédente, la solution de 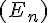 avec la condition initiale
avec la condition initiale 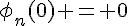 est donnée par
est donnée par 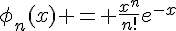 pour tout
pour tout 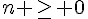 .
.
Partie B
1a. On a :
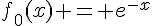

et 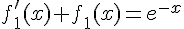 , donc
, donc 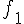 est solution de
est solution de 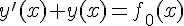 .
.
Soit 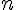 un entier strictement positif. Supposons que
un entier strictement positif. Supposons que 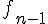 est solution de
est solution de 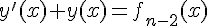 . Alors la solution
. Alors la solution  de
de 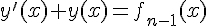 telle que
telle que 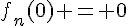 est donnée par la formule de la partie A :
est donnée par la formule de la partie A :
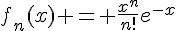
En effet, la solution générale de 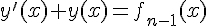 est de la forme
est de la forme 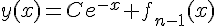 pour une constante
pour une constante 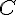 , et la condition
, et la condition 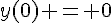 donne
donne 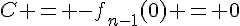 . On obtient ainsi que la solution
. On obtient ainsi que la solution  de
de 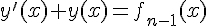 telle que
telle que 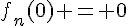 est donnée par :
est donnée par :
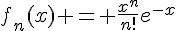
Ce résultat est vrai pour tout entier 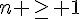 , donc
, donc 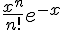 est la solution de
est la solution de 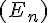 avec la condition initiale
avec la condition initiale 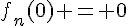 .
.
1b. Pour tout réel  , on a
, on a 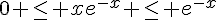 , donc par récurrence sur
, donc par récurrence sur 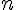 et par la question 1a, on obtient :
et par la question 1a, on obtient :
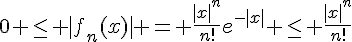
En intégrant ces inégalités sur l’intervalle ![[0,1]](https://mathovore.fr/latex-images/ccfcd347d0bf65dc77afe01a3306a96b.png) , on obtient :
, on obtient :
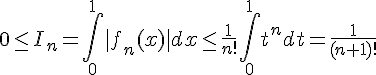
On en déduit que 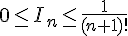 pour tout entier
pour tout entier 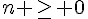 . En utilisant le théorème des croissances comparées, on obtient que
. En utilisant le théorème des croissances comparées, on obtient que 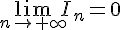 , donc la suite
, donc la suite 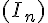 converge vers 0.
converge vers 0.
1c. Pour tout réel  , on a
, on a  , donc en intégrant ces inégalités sur l’intervalle
, donc en intégrant ces inégalités sur l’intervalle ![[0,1]](https://mathovore.fr/latex-images/ccfcd347d0bf65dc77afe01a3306a96b.png) , on obtient :
, on obtient :
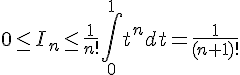
D’après la question précédente, la suite 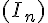 converge vers 0. En utilisant la question 2b, on a :
converge vers 0. En utilisant la question 2b, on a :
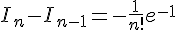
Donc la série  converge vers
converge vers 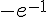 . D’après la question précédente, on a :
. D’après la question précédente, on a :
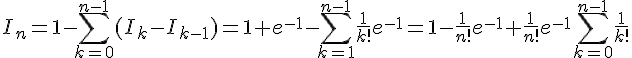
Ainsi, » 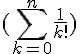 converge vers » align= »absmiddle » />e^{-1} + \lim_{n \to +\infty} I_n = e^{-1} + 0 = e » align= »absmiddle » />.
converge vers » align= »absmiddle » />e^{-1} + \lim_{n \to +\infty} I_n = e^{-1} + 0 = e » align= »absmiddle » />.
1d. Par définition, 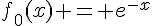 , donc la solution de
, donc la solution de 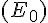 avec la condition initiale
avec la condition initiale 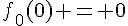 est
est 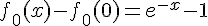 . D’après la question 2c de la partie A, la solution de
. D’après la question 2c de la partie A, la solution de 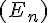 avec la condition initiale
avec la condition initiale 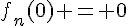 est
est 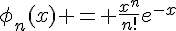 pour tout entier
pour tout entier 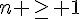 .
.
Exercice 17 :
a. On a 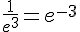 .
.
b. On a 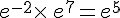 .
.
Exercice 18 :
On a 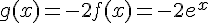 , donc
, donc 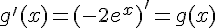 .
.
On a 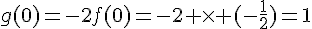 , donc
, donc 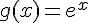 .
.
En utilisant 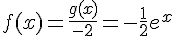 , on trouve que
, on trouve que 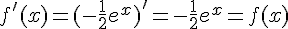 .
.
Exercice 19 :
1.
a. 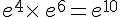 .
.
b. 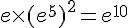 .
.
c. 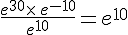 .
.
2.
a. 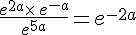 .
.
b.  .
.
c. 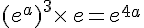 .
.
Exercice 20 :
1. On a 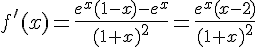 , donc l’équation de
, donc l’équation de 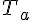 est
est  , ou
, ou  .
.
2. On cherche les valeurs de a pour lesquelles la droite passe par l’origine,
c’est-à-dire pour lesquelles 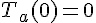 ,
,
c’est-à-dire pour lesquelles a=1, puisque 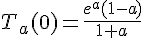 et que, pour
et que, pour 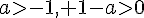 et
et 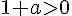 .
.
Donc il y a deux solutions : a=1 ou a=-2.
Exercice 21 :
1.
a. Avant la mise en marche, t=0, donc 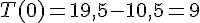 °C.
°C.
b. Après une journée de fonctionnement, 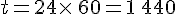 , donc
, donc 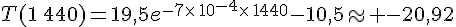 °C.
°C.
2. On a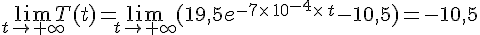 , donc la température moyenne tend vers -10,5°C quand le temps tend vers l’infini.
, donc la température moyenne tend vers -10,5°C quand le temps tend vers l’infini.
Exercice 22 :
1.
a. 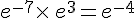 .
.
b. 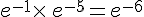 .
.
c. 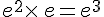 .
.
d. 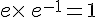 .
.
e. 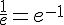 .
.
f. 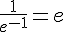 .
.
g. 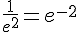 .
.
h. 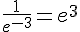 .
.
i. 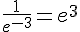 .
.
j. 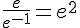 .
.
k. 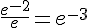 .
.
l. 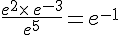 .
.
m.  .
.
n. 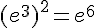 .
.
o. 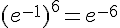 .
.
p. 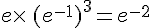 .
.
Exercice 23 :
1.
a. On a 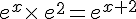 .
.
b. On a  .
.
c. 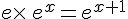 .
.
d. 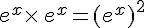 .
.
e. 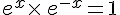 .
.
f.  .
.
g. 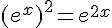 .
.
h. 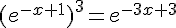 .
.
i. 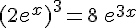 .
.
j. 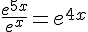 .
.
k. 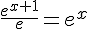 .
.
l. 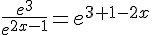 .
.
Exercice 24 :
1.
a. On a 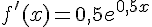 .
.
b. On a 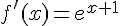 .
.
c. On a  .
.
2.
a. On a 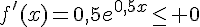 pour
pour  , donc f est décroissante sur
, donc f est décroissante sur 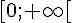 .
.
b. On a 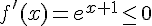 pour
pour 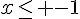 , donc f est décroissante sur
, donc f est décroissante sur ![]-\infty;-1]](https://mathovore.fr/latex-images/92c5730fc4afe15926037d88ab2b15b3.png) .
.
c. On a  pour tout x, donc f est croissante sur
pour tout x, donc f est croissante sur  .
.
Exercice 25 :
1. On a 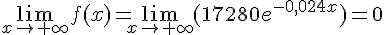 , donc la limite de f en
, donc la limite de f en  est 0.
est 0.
2. On a 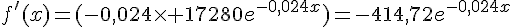 , qui est strictement négative sur
, qui est strictement négative sur 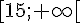 , donc f est décroissante sur cet intervalle.
, donc f est décroissante sur cet intervalle.
3. La conjecture est que la fonction f est décroissante sur  , ce qui est effectivement vrai d’après 2.
, ce qui est effectivement vrai d’après 2.
En effet, la dérivée est strictement négative sur tout l’intervalle de définition de f, donc f est décroissante sur cet intervalle.
Exercice 26 :
1. On a 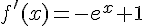 .
.
2. On a 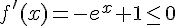 pour tout
pour tout 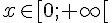 , donc f est décroissante sur cet intervalle.
, donc f est décroissante sur cet intervalle.
3. On sait que f est décroissante sur 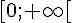 , donc son maximum est atteint en x=0 et son minimum en
, donc son maximum est atteint en x=0 et son minimum en 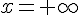 .
.
On peut calculer f(0)=2 et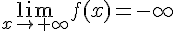 .
.
On a également 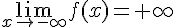 (car
(car 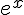 tends vers 0 plus vite que x tend vers -∞) et f est décroissante sur
tends vers 0 plus vite que x tend vers -∞) et f est décroissante sur ![]-\infty;0]](https://mathovore.fr/latex-images/07a377ef53def0586728ce11eb667298.png) .
.
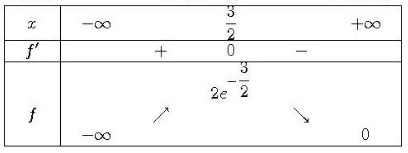
Donc le tableau de variation de f est :
x | ![]-\infty;0]](https://mathovore.fr/latex-images/07a377ef53def0586728ce11eb667298.png) | 0 |
| 0 | 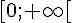
f'(x) | + | 0 | –
f(x) |  | 2 |
| 2 | 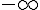
Exercice 27 :
1.
a. On a  .
.
b. On a 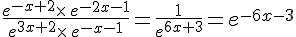 .
.
c. On a 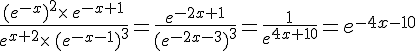 .
.
Exercice 28 :
1.
On a 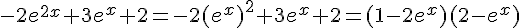 .
.
2.
On a 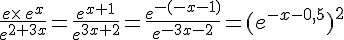 .
.
3.
On a  .
.
Exercice 29 :
1) En posant 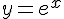 , on peut réécrire l’équation
, on peut réécrire l’équation 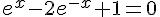 sous la forme
sous la forme 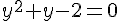 .
.
Cette dernière équation correspond à une équation du second degré se factorisant en 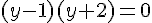 .
.
Donc, on a 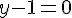 ou
ou 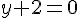 , c’est-à-dire
, c’est-à-dire 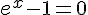 ou
ou 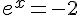 .
.
Or, 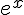 est toujours strictement positif, donc on ne peut pas avoir
est toujours strictement positif, donc on ne peut pas avoir 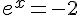 .
.
Ainsi, l’équation 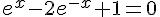 est équivalente à l’équation
est équivalente à l’équation 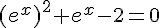 .
.
2) On vient de montrer que 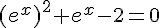 est équivalente à
est équivalente à 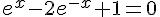 .
.
On peut donc résoudre l’équation 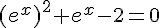 .
.
En posant 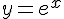 , on a
, on a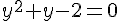 , qui correspond à une équation du second degré se factorisant en
, qui correspond à une équation du second degré se factorisant en 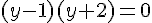 .
.
Ainsi, on a 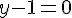 ou y+2=0, c’est-à-dire
ou y+2=0, c’est-à-dire 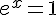 ou
ou 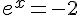 .
.
Or, e^x ne peut pas être négatif, donc on ne peut pas avoir 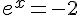 .
.
D’où la solution de l’équation 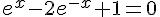 est
est 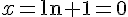 .
.
Exercice 30 :
1) On peut réécrire l’inéquation 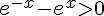 sous la forme
sous la forme 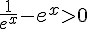 , c’est-à-dire
, c’est-à-dire 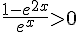 . Ainsi, on a deux cas à étudier :
. Ainsi, on a deux cas à étudier :
– Si 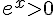 , alors l’inéquation équivaut à
, alors l’inéquation équivaut à 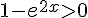 , c’est-à-dire
, c’est-à-dire 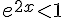 , d’où x<0.
, d’où x<0.
– Si 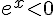 , alors l’inéquation équivaut à
, alors l’inéquation équivaut à 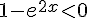 , c’est-à-dire
, c’est-à-dire 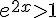 , d’où
, d’où  .
.
Finalement, la solution de l’inéquation 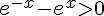 est x<0.
est x<0.
2) On peut réécrire 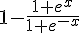 sous la forme
sous la forme 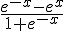 .
.
On vient de montrer que 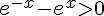 pour tout
pour tout 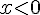 , donc le numérateur est négatif dans cette intervalle.
, donc le numérateur est négatif dans cette intervalle.
De plus, le dénominateur est toujours positif.
Ainsi,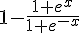 est négatif sur
est négatif sur 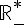 .
.
Exercice 31 :
Conjecture : On a 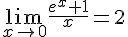 et
et 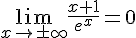 .
.
Démonstration :
– Pour la limite en 0, on peut utiliser le développement limité de 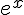 au premier ordre au voisinage de 0 :
au premier ordre au voisinage de 0 : 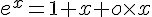 .
.
Ainsi, on a 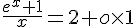 , d’où
, d’où 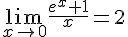 .
.
– Pour la limite en  , on a
, on a 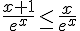 , qui tend vers 0 quand x tend vers
, qui tend vers 0 quand x tend vers  .
.
– Pour la limite en 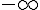 , on peut réécrire
, on peut réécrire 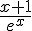 sous la forme
sous la forme  , qui tend vers 0 quand x tend vers
, qui tend vers 0 quand x tend vers 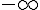 .
.
En effet, on a 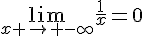 et
et 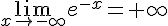 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonction exponentielle : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de première
Cours de première
Exercices de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.