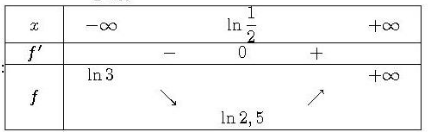
Exercice 1 :
Exercice 2 :
Simplifier les expressions suivantes :
Exercice 3 :
Soit n un entier naturel non nul et a un nombre réel strictement positif.
Exercice 4 :
Etudier les limites suivantes :
a.
b.
c.
d.
d.
e.
f.
Exercice 5 :
Exercice 6 :
Résoudre dans chacune des équations suivantes :
a.
b.
c.
d.
e.
Posons
Exercice 7 :
Exercice 8 :
Déterminer la fonction dérivée de la fonction f sur l’ensemble
a.
b.
c.
Exercice 9 :
Si a est un zéro de P(z) alors on doit avoir :
soit
soit le système d’équations
On constate facilement que 2 vérifie simultanément les deux équations c’est la valeur cherchée.
On écrit donc, b et c étant des complexes
Et par identification
et
et
On est conduit à résoudre l’équation du second degré à coefficients complexes :
D’où les deux racines
et
et
donc
Exercice 10 :
Résoudre les inéquations suivantes :
Exercice 11 :
Résoudre les équations suivantes :
Calculons le discriminant :
, il y a deux racines réelles distinctes .
Exercice 12 :
Résoudre les équations suivantes :
Exercice 13 :
Simplifier :
Exercice 14 :
Exercice 15 :
1. ln(3-5x) = 0 équivaut à . Donc 5x = 2 et x = 2/5.
2. On peut transformer l’équation de la manière suivante :
En utilisant la propriété ln(a)-ln(b) = ln(a/b), on obtient :
Cela équivaut à , soit
.
On résout cette équation du second degré en x et on vérifie que les solutions obtenues sont bien positives et différentes de 4.
3. équivaut à
, donc (x+4)(x+1) = 6.
On résout cette équation du second degré en x et on vérifie que la solution obtenue est bien positive.
4. signifie que
, c’est-à-dire que (x+4)(x+1) = 6 ou (x+4)(x+1) = -6. On résout ces deux équations et on vérifie que les solutions obtenues sont bien positives.
5. On peut réécrire l’équation sous la forme .
En posant y = ln x, cela équivaut à , soit
.
On peut factoriser cette expression en , donc y = 2 ou y = (-1±i√3)/2. On vérifie que ces trois valeurs de y correspondent à des solutions de l’équation initiale.
6. équivaut à
(car ln est une fonction strictement croissante).
On résout cette inéquation et on trouve 1/3 < x < -1/5.
7. On peut réécrire l’équation sous la forme .
On pose y = ln x et on note f(y) = y – (1/y).
L’équation devient f(y) < 3/2.
On étudie la fonction f(y) : elle est dérivable sur ]0,+∞[, sa dérivée est , donc f est strictement croissante sur ]0,+∞[.
De plus, f(1) = 0. On en déduit que l’équation est équivalente à
.
On calcule en résolvant l’équation
en x :
La solution positive est , donc
.
On calcule et on trouve
.
Finalement, les solutions de l’inéquation sont les x tels que , c’est-à-dire
.
Exercice 16 :
On peut comparer ces deux nombres en regardant la fonction , pour x > 0.
On a , donc f est croissante sur ]0,e[ et décroissante sur ]e,+∞[.
En particulier, f( e^(1/e) ) ≈ 1,44 est le maximum de f sur ]0,+∞[.
On a donc :
La dernière égalité est justifiée par le fait que f(e) > f(\pi) pour 0 < x < e^(1/e) et que f(x) < f(e) pour x > e^(1/e).
Finalement, on a :
Le nombre est donc plus grand que
.
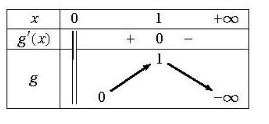
Exercice 17 :
g est dérivable sur son ensemble de définition en tant que somme de
fonctions dérivables sur cet intervalle .
Conclusion : sur , f est croissant sur
.
Exercice 18 :
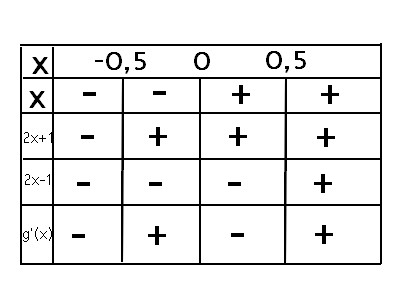
1.Calculer la dérivée de la fonction g et étudier son signe. En déduire les variations de la fonction g .
Le signe de est celui de
.
sur
.
donc g est strictement décroissante sur .
2. Calculer g(1). En déduire le signe de g(x) pour x appartenant à l’intervalle ]0;+  [ .
[ .
g est strictement décroissante sur et
.
Conclusion : g est positive ou nulle sur ]0;1] et négative sur .
Exercice 19 :
1) simplifier
2) Déterminer le plus petit entier n tel que 1,05 n 1,5
1,5
La fonction ln est strictement croissante sur ..
(ln 1,05 <0)
3) Chaque année, la population d’une ville diminue de 3%. Au bout de combien d’année, la population de cette ville aura-t-elle diminué de plus de 30%
Exercice 20 :
Partie A:
1. Limites de la fonction g en 0 et :
Pour la limite en 0, on peut utiliser le développement de Taylor de ln(x) au premier ordre, qui est près de x=0.
Ainsi, en utilisant ce développement dans la définition de g, on obtient:
Comme est une infinitésimale de plus haut ordre que x, on a
, ce qui implique que
.
Pour la limite en , on peut utiliser le lemme de L’Hôpital.
En effet, on a:
.
En appliquant le lemme de L’Hôpital, on obtient:
Donc, la limite de g en est 0.
2. Calcul de la dérivée de g(x) et justification de la dérivabilité de g sur l’intervalle :
On peut calculer la dérivée de g(x) en utilisant la formule de dérivation de la différence. On a:
Ainsi, g'(x) = -ln(x).
Pour montrer que g est dérivable sur l’intervalle , il suffit de montrer que la limite du taux d’accroissement de g(x) quand x tend vers a pour tout a>0 existe et est finie. On a:
Donc, la fonction g est dérivable sur l’intervalle .
3. Tableau de variations de la fonction g:
Pour dresser le tableau de variations de g(x), on peut utiliser sa dérivée g'(x). On a:
– g'(x) est définie et strictement négative sur ].
– g'(x) est décroissante sur .
– Le signe de g'(x) change en x=1, donc g(x) atteint son minimum en x=1.
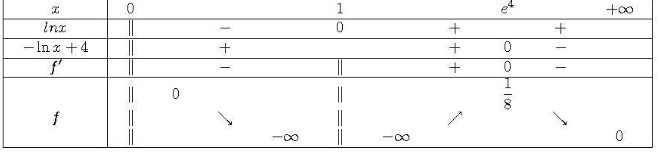
On obtient alors le tableau de variations suivant pour g(x):
x | 0 | 1 | +\infty
——-|——-|———|——–
g'(x) | – | 0/- | 0
g(x) | 0 | -1/e + 1 | 0
Partie B:
1. Conjecture de sens de variation et de limite de la suite :
a. Pour conjecturer le sens de variation de la suite , on peut calculer les premiers termes de la suite et observer s’ils augmentent ou diminuent. On a:
On peut remarquer que la suite diminue et atteint des valeurs de plus en plus petites.
b. Pour conjecturer la limite de la suite , on peut observer que les termes de la suite décroissent vers 0 à mesure que n augmente.
On peut également utiliser la règle de Stolz-Cesàro pour montrer que la limite de est 0. En effet, on a:
Donc, la limite de est 0.
2. Calcul de la suite et détermination de son sens de variation:
a. On peut calculer en utilisant la formule de
.
On a:
.
b. Pour déterminer le sens de variation de la suite , on peut étudier le signe de sa dérivée
.
On observe que la dérivée est positive pour n=1 et décroissante sur , donc la suite
est décroissante sur
.
3. Montrer que la suite est bornée:
On peut montrer que la suite est bornée en utilisant l’inégalité de Bernoulli
pour tout x>-1 et tout entier naturel n. On a:
Ainsi, la suite est majorée par e et donc bornée.
4. Montrer que la suite est convergente et déterminer sa limite:
On peut utiliser le théorème de Bolzano-Weierstrass pour montrer que la suite admet une limite. En effet, comme on a montré que la suite
est bornée, elle admet une sous-suite convergente.
On peut également utiliser la propriété des suites adjacentes pour déterminer la limite de .
Pour cela, on construit deux suites et
telles que
et
.
On peut prendre par exemple:
– pour tout n, et
pour tout n (on a montré que u_n ≤ e pour tout n).
– On a
Donc, la suite converge vers la limite commune des deux suites adjacentes
et
, qui est 0.
Exercice 21 :
1. Démonstration de :
On a f(x) = ln(2^x) – ln(x^2) = xln2 – 2lnx par les propriétés des logarithmes.
2. Calcul de f(2) et f(4):
On a .
De même, on a .
3. Calcul de la dérivée f ‘ de f:
On peut calculer la dérivée de f(x) en utilisant la formule de dérivation de la différence et les propriétés des logarithmes. On a:
.
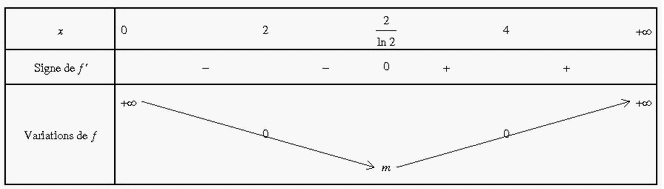
4. Signe de f(x):
Pour déterminer le signe de f(x), on peut étudier le signe de sa dérivée f ‘(x):
– f ‘(x) est définie et strictement négative sur .
– f ‘(x) est décroissante sur .
On en déduit que la fonction f est décroissante sur .
En particulier, pour tout x>2, on a .
5. Ensemble des entiers n pour lesquels :
On peut réécrire cette inégalité sous la forme d’une exponentielle: .
On remarque que les deux membres de l’inégalité sont des fonctions croissantes de n pour n > 0, donc l’inégalité est vraie pour un nombre fini d’entiers.
On peut ensuite vérifier pour chacun des entiers n si l’inégalité est vraie.
Par exemple, pour n=1, on a , donc l’inégalité est vraie pour n=1.
De même, pour n=2, on a , donc l’inégalité est vraie pour n=2.
Pour n=3, on a , donc l’inégalité est vraie pour n=1, 2 et 3.
On peut poursuivre le raisonnement pour les valeurs suivantes de n, jusqu’à trouver le plus grand entier satisfaisant l’inégalité:
– Pour n=4, on a , donc l’inégalité est vraie pour n=1, 2, 3 et 4.
– Pour n=5, on a , donc l’inégalité est vraie pour n=1, 2, 3, 4 et 5.
– Pour n=6, on a , donc l’inégalité est vraie pour n=1, 2, 3, 4, 5 et 6.
– Pour n=7, on a , donc l’inégalité est vraie pour n=1, 2, 3, 4, 5, 6 et 7.
On peut ensuite remarquer que pour tout entier n ≥ 8, on a , donc l’inégalité n’est plus vraie. Ainsi, l’ensemble des entiers n pour lesquels on a
est {1, 2, 3, 4, 5, 6, 7}.
Exercice 22 :
a) La seule solution est x=0 car .
b) On a qui donne
.
c) On résout l’équation , donc
qui donne x=ln2.
d) On résout l’équation , donc
qui donne
.
e) On résout l’équation , donc
qui donne
et finalement
.
f) L’équation n’a pas de solution car est toujours positif.
Exercice 23 :
a) On a .
b) On a .
c) On résout l’équation , donc
, ce qui donne x=e^{7/2}.
d) On résout l’équation , donc
, ce qui donne
.
e) On a x=1/e.
f) On résout l’équation , donc
, ce qui donne
ou
(mais cette dernière solution est exclue car elle n’appartient pas à l’ensemble de définition de ln).
Exercice 24 :
a) On peut simplifier .
b) On peut simplifier .
c) On peut simplifier .
Exercice 25 :
a) L’ensemble de définition est ]-∞; -1[ ∪ ]1; +∞[. On peut simplifier , donc l’équation est équivalente à
, donc
, ce qui donne
.
Cependant, x=√(21/25) ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=-√(21/25)=-√21/5.
b) L’ensemble de définition est ]3/2; +∞[.
On peut simplifier ,
donc x(x-3)=4 et finalement x=4 ou x=-1.
Cependant, x=-1 ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=4.
c) L’ensemble de définition est ]0; 3[.
On peut simplifier , donc
et finalement
ou x=2.
Cependant, x=2 ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=1/2.
Exercice 26 :
1. On a
, donc f(x) tends vers -∞ quand x tends vers 0 car tends vers -∞.
On peut interpréter graphiquement ce résultat en disant que admet une asymptote verticale en x=0.
2. a) On a f(x) tends vers +∞ quand x tends vers +∞ car 2x-1 tends vers +∞ et ln(x/(x+1)) tends vers 0.
b) On a
, donc y=2x-1 est une asymptote oblique à en +∞.
On peut dire que est située en dessous de la droite y=2x-1 car
pour tout x.
3. On résout l’inéquation , donc
, ce qui donne x≤0. On peut également écrire l’inéquation sous la forme
, c’est à dire x≥0, mais cette solution n’appartient pas à l’ensemble de définition de ln.
4. On cherche à résoudre l’équation .
On peut réécrire l’équation sous la forme , donc
, ce qui donne l’équation
.
On sait que l’équation a une unique solution dans car
est une fonction croissante dans cet intervalle (puisque sa dérivée est
).
En utilisant la méthode de dichotomie, on trouve que la solution est .
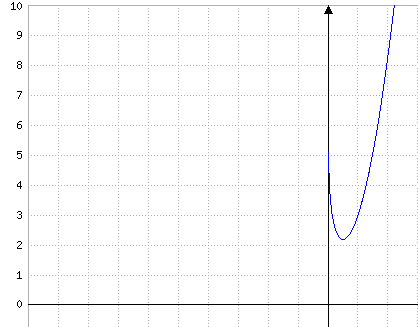
5. Voir figure ci-dessous.
Exercice 27 :
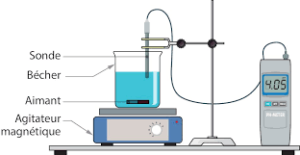
1. On a , donc la solution est basique.
Si la concentration en ions est égale à 0,1 mol/L, alors pH=-log(0,1)≈1 (la solution est acide).
2. Une solution neutre a un pH égal à 7.
On a , donc
mol/L.
3. Si l’on augmente la concentration en ions H_3O^+, on diminue le pH de la solution car , donc une concentration plus élevée implique un logarithme plus petit (et donc un pH plus petit).
4. Pour incrémenter le pH d’une solution, il faut ajouter une base (qui réagit avec les ions pour les neutraliser) ou enlever un acide (qui libère des ions
dans la solution). Pour décrémenter le pH d’une solution, il faut faire l’opposé (ajouter un acide ou enlever une base).
VOCABULAIRE : Décrémenter, c’est soustraire 1.
Exercice 28 :
1. a) On a car
tends vers 0 et ln tends vers
quand son argument tend vers 0.
b) En utilisant la règle de l’Hôpital, on trouve que .
Donc l’équation de l’asymptote oblique est pour une certaine constante c.
En utilisant l’expression qui est équivalente à
, on trouve que c=1.
Donc l’asymptote oblique est .
c) En utilisant l’expression , on trouve que
, donc l’axe des ordonnées est un axe de symétrie pour C.
d) On a
car x+2 tends vers +∞ et tends vers -∞.
Donc il y a une seconde asymptote oblique en +∞.
En utilisant , on trouve que l’équation de cette asymptote est y=-2x.
2. On a , donc C est symétrique par rapport à l’axe des ordonnées.
3. On résout l’équation comme dans l’exercice précédent et on trouve
.
4. On calcule la dérivée de f : où
.
La fonction est décroissante car sa dérivée est
pour t>0.
Donc pour tout x, ce qui implique que f est décroissante sur
.
De plus, f(-x)=f(x), donc C est symétrique par rapport à l’axe des ordonnées et il suffit d’étudier les variations de f sur .
On a et
, donc C intersecte l’axe des abscisses en un unique point
.
Pour déterminer son encadrement d’amplitude , on utilise la méthode de dichotomie.
On trouve que est plus grand que 0,69 et plus petit que 0,70.
5. Voir figure ci-dessous.