Exercice 1 :
Soit le nombre de filles le nombre de garçons est
.
Conclusion : il y a 15 filles et 10 garçons dans cette classe .
Exercice 2 :
hauteur en (m) 1.2 1.3 1.4 1.5 1.6
Effectif 21 37 51 22 14
1. Calculer la moyenne de cette série .
La taille moyenne est de 1,38 mètre .
2. Déterminer la médiane de cette série .
145 est un nombre impair, il faut donc regarder la 73 ème valeur .
La médiane est 1,4 .
3. Interpréter les résultats obtenus précédemment .
Si tous les éléments avaient la même taille, chaque élément aurait une hauteur de 1,38 mètre .
Il y a autant d’élément qui ont une hauteur supérieure à 1,4 mètre qu’inférieurs à 1,4 mètre .
Exercice 3 :
groupe de personnes
tailles en cm 130 145 155 160 170 175 180 190
effectifs 3 5 11 25 36 20 8 2
effectifs cumules
1) calculer la taille moyenne de ces personnes
2) Calculer le premier quartile Q1 ,la médiane et le troisième quartile Q3 de cette serie.
Pour le 1er quartile :
L’effectif total est 110
Il faut donc regarder la 28éme valeur.
Pour la médiane :
110 est paire donc il faut faire la moyenne de la 55ème et 56ème valeur.
donc la médiane est de 170 cm .
Pour le 3ème quartile :
Il faut donc regarder la 83 ème valeur .
3) Calculer l’étendue de la série initiale des tailles ?
190-130=60 cm
Exercice 4 :
| 10 | 20 | 30 | 40 | 50 | 60 |
| 15 | 25 | 35 | 45 | 55 | 65 |
| 240 | 628 | 556 | 370 | 356 | 190 |
1er ligne : Age noté « a »
2eme ligne : Centre des classe
3eme ligne : Effectifs
Pendant les vacances de Noël mr GLISSSE est parti skier à L’alpe d’hurez .Pendant une heure, on a relevé l’age des personnes qui sont montée dans un telesiege ( voir le tableau)
1)Calculer le nombre de personnes ayant pris le télésiège pendant cette heure.
N=240+628+556+370+356+190=2 340 personnes
2)Compléter la 2eme ligne du tableau .
Voir le tableau
3)Calculer l’age moyen des skieurs Arrondir le resultat a l’unité.
Conclusion : l’âge moyen des skieurs est de 37 ans.
Exercice 5 :
Voici les notes obtenues par 13 élèves à un devoir de mathématiques :
8;9;19;17;6;18;18;8;14;12;9;10;11
1. calculer la moyenne arrondie au centième de cette série de notes .
2. calculer le pourcentage d’élèves qui ont une note supérieure à cette moyenne de la classe .
les notes supérieures à la moyenne de la classe sont :19,17,18,18,14
Il y a 5 notes
3. déterminer la médiane de cette série de notes .
6;8;8;9;9;10;11;12;14;17;18;18;19
Il y 13 notes , 13 est impair donc la médiane est la 7ème valeur.
La médiane est 11 .
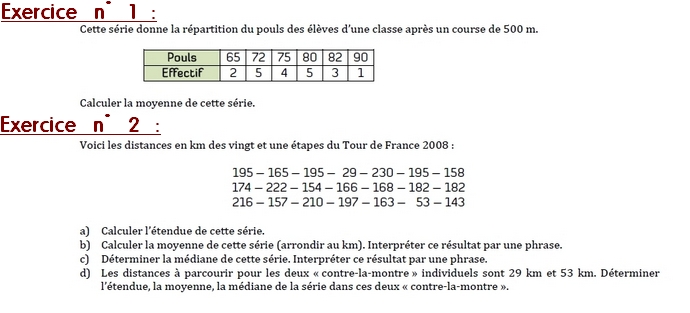
Exercice 6 :
La moyenne du poul des élèves est de 76,3
Exercice 7 :
a) 230-29=201
L’étendue est de 201 km.
b)
Si toutes les étapes avaient la même longueur, chaque étape aurait une distance de 169 km.
c) Rangeons les valeurs par ordre croissant :
29-53-143-154-157-158-163-165-166-168-174-182-182-195-195-195-197-210-216-222-230-
Il y a 28 valeurs et 21 est un nombre impair
donc la médiane est la 11ème valeur soit 174 km .
d) L’étendue est 53-29 = 24 km
La moyenne est (53+29):2=82:2=41 km .
La médiane est aussi la moyenne.
Exercice 8 :
1.
Exercice 9 :
1.
Interprétation :
Si l’athlète avait effectué tous les mêmes lancers, il aurait effectué des lancers de 18,7 mètres.
2.
Il y a 12 valeurs et 12 est pair, donc faisons la moyenne de la sixième et septième valeur.
Interprétation :
Il y a autant de lancers en-dessous de 19 mètres qu’au dessus.
Exercice 10 :
Il y a deux correcteurs au brevet des collèges:
le premier a 11 de moyenne avec 55 candidats et son collègue n’a que 9,5 de moyenne avec 45 candidats.
Quelle est la moyenne générale.
Exercice 11 :
Les gendarmes ont effectué un contrôle de vitesse sur le bord d’une route nationale.
| vitesse | [50;70[ | [70;90[ | [90;110[ | [110;130[ |
| effectif | 15 | 90 | 35 | 5 |
Calculer la vitesse moyenne des automobilistes contrôlés.
Exercice 12 :
La Polynésie française compte 219 500 habitants.
Leur répartition géographique est repré-sentée par le diagramme circulaire suivant:
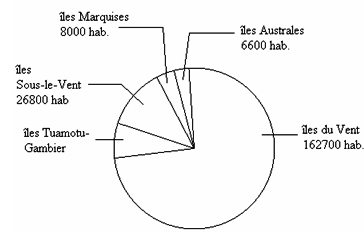
a. calculer le nombre d’habitants des îles Tuamotu-Gambier.
b. calculer le pourcentage des habitants des îles Sous-le-Vent par rapport à la population totale.
Exercice 13 :
| France | Belgique | Italie | Espagne | Autres | |
| nombre de victoires | 36 | 18 | 9 | 9 | 13 |
| fréquence (en pourcent) |
Exercice 15 :
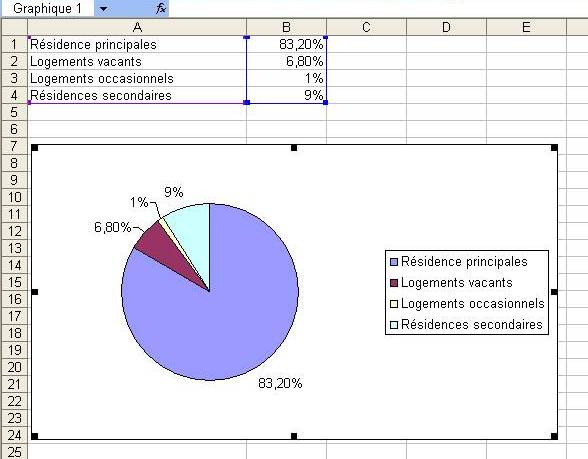
Ce tableau donne la répartition des 29 495 000 logements en France selon leur catégorie.
| Catégorie | Fréquence (en %) |
| Résidence principales | 83,2 |
| Logements vacants | 6,8 |
| Logements occasionnels | 1 |
| Résidences secondaires | 9 |
1. Représenter cette distribution de fréquences par un diagramme circulaire .
2.Calculer le nombre de logements de chaque catégorie en arrondissant au millier .
| Catégorie | Nombre de logements |
| Résidence principales | 24 539 840 |
| Logements vacants | 2 005 660 |
| Logements occasionnels | 294 950 |
| Résidences secondaires | 2 654 550 |
Exercice 17 :
a. L’étendue pour le salaire des femmes est : 3470-1044=2426.
Cela signifie que l’écart entre le plus haut et le plus bas salaire pour les femmes est de 2 426 euros .
L’étendue pour le salaire des hommes est : 2096-1002=1094.
Cela signifie que l’écart entre le plus haut et le plus bas salaire pour les hommes est de 1 094 euros.
b.
Le salaire moyen pour les femmes est :
€
Le salaire moyen pour les hommes est :
€
Exercice 21 :
notes 6 7 9 10 11 12 14 15 16 19
effectifs 3 4 4 2 1 3 2 4 1 2
1) Il y a eu 2+1+3+2+4+1+2=15 élèves qui ont eu la moyenne sur 26 élèves.
soit 57,69 % .
2) 26 est un nombre pair, la médiane est la moyenne de la 13ème et 14ème valeur soit (11+12):2=11,5 .
3a) soit la 7ème valeur .
soit la 20 ème valeur .
3b) Il y a 3 + 4 + 4 + 2 + 1 + 3 = 17 élèves qui ont eu une note inférieure à 12 .
soit à peu près 65 % .
Exercice 22 :
Une personne affirme que 25% des accidents se produisent entre 20h et 24h. Cette affirmation est t elle vraie ? Justifier la réponse.
(4581 accidents se sont produits entre 8h et 9h)
Les nombres de 20 à 23h ( il n’y a pas 24h dans le tableau) :
Entre 20h et 23h
Il y a 5+3+3=11 % des accidents qui se produisent donc la personne a tort .
Exercice 23 :
» Voici les températures moyennes mensuelles de deux villes, en degrés Celsius :
MEXICO
J F M A M J
12,4 14,1 16,2 17,4 18,4 17,7
J A S O N D
16,7 16,8 16,3 15,1 13,9 12
BARCELONE
J F M A M J
9,5 10,3 12,4 14,6 17,7 21,5
J A S O N D
24,3 24,3 21,8 17,6 13,5 10,3
1- Pour chacune de ces villes:
a-Calculer l’ étendue de la série des températures ;
Pour Mexico : 18,4- 12,4 = 6°C
Pour Barcelone : 24,3 – 9,5 = 14,8 °C
b- Estimer la température moyenne annuelle ;
Pour mexico :
Pour Barcelone :
Exercice 24 :
Kevin dit a sa soeur » en moyenne, on est mieux payé chez KALU »
Qu’en pensez vous ?
Calculons la moyenne chez HITI :
€
Calculons le salaire moyen chez KALU :
€
Conclusion : les salariés sont, en moyenne, mieux payés chez HITI donc Kevin a tord.
Exercice 25 :
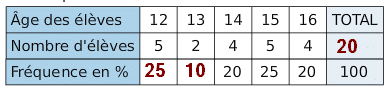
Taraina dirige une école de danse pour adolescents. Elle a relevé dans un tableau l’âge de ses élèves, ainsi que la fréquence des âges.
- Compléter le tableau suivant :
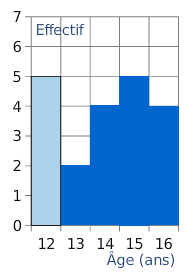
2. Ci-dessous, compléter le diagramme en barre des effectifs.
- Quelle est, dans cette école, la fréquence des élèves ayant 14 ans ?
La fréquence des élèves ayant 14 ans est de 20 %.
2.Quelles sont l’étendue et la médiane de cette série statistiques ?
L’étendue est de 16-12=4 et l’effectif total est pair donc la médiane est la moyenne entre la dixième et la onzième valeur du caractère.
Médiane = 14.