Les équations différentielles : corrigé des exercices de maths en terminale en PDF.

Mis à jour le 18 septembre 2025

🔍Corrigés Détaillés

Terminale • Lycée

Les équations différentielles

🔎 Analyse : 15 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Exercices de mathématiques en terminale sur les équations différentielles.

Exercice 1 :

Résoudre les équations différentielles suivantes :

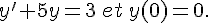
1. $y'+5y=3\,et\,y(0)=0.$

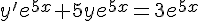
$y'e^{5x}+5ye^{5x}=3e^{5x}$

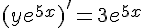
$(ye^{5x})'=3e^{5x}$

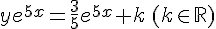
$ye^{5x}=\frac{3}{5}e^{5x}+k\,(k\in \mathbb{R})$

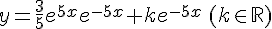
$y=\frac{3}{5}e^{5x}e^{-5x}+ke^{-5x}\,(k\in \mathbb{R})$

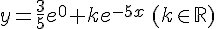
$y=\frac{3}{5}e^{0} +ke^{-5x}\,(k\in \mathbb{R})$

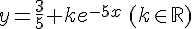
$y=\frac{3}{5} +ke^{-5x}\,(k\in \mathbb{R})$

or nous avons y(0) = 0.

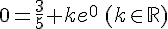
$0=\frac{3}{5} +ke^{0}\,(k\in \mathbb{R})$

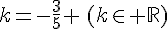
$k=-\frac{3}{5} \,(k\in \mathbb{R})$

Conclusion : 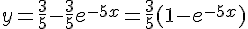$y=\frac{3}{5}-\frac{3}{5}e^{-5x}=\frac{3}{5}(1-e^{-5x})$

Exercice 2 :
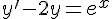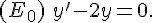
Soit (E) l’équation différentielle $y'-2y=e^x$ et $(E_0)\,\,y'-2y=0.$

1. Vérifier que la fonction définie par 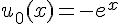$u_0(x)=-e^x$ est solution de (E) .

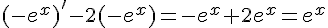
$(-e^x)'-2(-e^x)=-e^x+2e^x=e^x$

donc 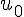$u_0$ est solution de (E).

2. Résoudre l’équation différentielle (Eo) .

$y'-2y=0$

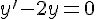
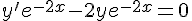
$y'e^{-2x}-2ye^{-2x}=0$

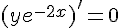
$(ye^{-2x})'=0$

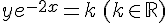
$ye^{-2x}=k\,(k\in\mathbb{R})$

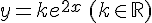
$y=ke^{2x}\,(k\in\mathbb{R})$

3. Montrer que u est solution de (E) 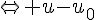$\Leftrightarrow u-u_0$ est solution de (Eo) .

à montrer……

4. En déduire les solutions de (E) .

Les solutions de (E) sont du type : $y=-e^x+ke^{2x}\,(k\in\mathbb{R})$

5. Déterminer la solution f de (E) qui s’annule en 1 .

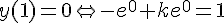
$y(1)=0\Leftrightarrow -e^0+ke^{0}=1$

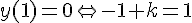
$y(1)=0\Leftrightarrow -1+k=1$

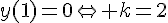
$y(1)=0\Leftrightarrow k=2$

donc

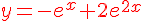
${\color{DarkRed} y=-e^x+2e^{2x} }$

Exercice 3 :
Déterminer la solution de 2y ‘ + y = 1 telle que y(1) = 2 .

$2y'+y=1$

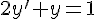
Divisons par 2 chaque membre de cette équation.

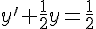
$y'+\frac{1}{2}y=\frac{1}{2}$

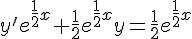
$y'e^{\frac{1}{2}x}+\frac{1}{2}e^{\frac{1}{2}x}y=\frac{1}{2}e^{\frac{1}{2}x}$

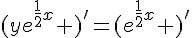
$(ye^{\frac{1}{2}x} )'= (e^{\frac{1}{2}x} )'$

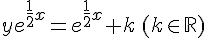
$ye^{\frac{1}{2}x} =e^{\frac{1}{2}x}+k\,(k\in\mathbb{R})$

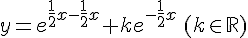
$y =e^{\frac{1}{2}x-\frac{1}{2}x}+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

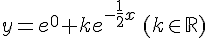
$y =e^{0}+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

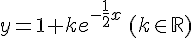
$y =1+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

or nous avons 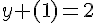$y (1)=2$

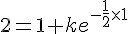
$2=1+ke^{-\frac{1}{2}\times 1}$

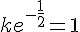
$ke^{-\frac{1}{2}}=1$

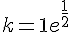
$k=1e^{\frac{1}{2}}$

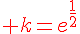
${\color{DarkRed} k=e^{\frac{1}{2}}}$

Conclusion :

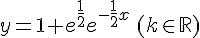
$y =1+e^{\frac{1}{2}}e^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

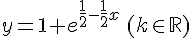
$y =1+e^{\frac{1}{2}-\frac{1}{2}x}\,(k\in\mathbb{R})$

${\color{DarkRed} y =1+e^{\frac{1}{2} (1-x )}\,(k\in\mathbb{R}})$

Exercice 4 :
Déterminer la solution de 2y ‘ + y = 1 telle que y(1) = 2 .

$2y'+y=1$

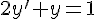
Divisons par 2 chaque membre de cette équation.

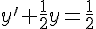
$y'+\frac{1}{2}y=\frac{1}{2}$

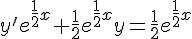
$y'e^{\frac{1}{2}x}+\frac{1}{2}e^{\frac{1}{2}x}y=\frac{1}{2}e^{\frac{1}{2}x}$

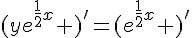
$(ye^{\frac{1}{2}x} )'= (e^{\frac{1}{2}x} )'$

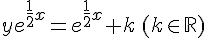
$ye^{\frac{1}{2}x} =e^{\frac{1}{2}x}+k\,(k\in\mathbb{R})$

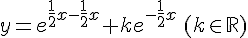
$y =e^{\frac{1}{2}x-\frac{1}{2}x}+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

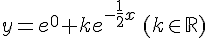
$y =e^{0}+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

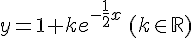
$y =1+ke^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

or nous avons 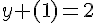$y (1)=2$

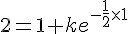
$2=1+ke^{-\frac{1}{2}\times 1}$

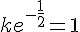
$ke^{-\frac{1}{2}}=1$

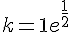
$k=1e^{\frac{1}{2}}$

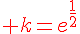
${\color{DarkRed} k=e^{\frac{1}{2}}}$

Conclusion :

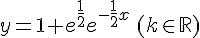
$y =1+e^{\frac{1}{2}}e^{-\frac{1}{2}x}\,(k\in\mathbb{R})$

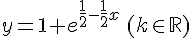
$y =1+e^{\frac{1}{2}-\frac{1}{2}x}\,(k\in\mathbb{R})$

${\color{DarkRed} y =1+e^{\frac{1}{2} (1-x )}\,(k\in\mathbb{R}})$

Exercice 5 :

1. Résoudre l’équation différentielle(E) : y ‘ = – 2y .
$y'+2y=0$

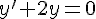
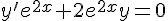
$y'e^{2x}+2e^{2x}y=0$

$(ye^{2x} )'=0$

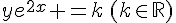
$ye^{2x} =k\,(k\in\mathbb{R})$

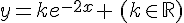
$y=ke^{-2x} \,(k\in\mathbb{R})$

2. En déduire la solution de (E) dont la courbe représentative admet, au point d’abscisse 0,
une tangente parallèle à la droite d’équation y = – 4x + 1.

cela signifie que y'(0)= – 4

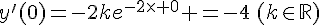
$y'(0)=-2ke^{-2\times 0} =-4\,(k\in\mathbb{R})$

$-2k=-4$

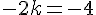
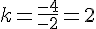
$k=\frac{-4}{-2}=2$

Conclusion : 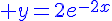${\color{DarkBlue} y=2e^{-2x}}$

Exercice 6 :

1. Résoudre l’équation différentielle (E) : y ‘ = 3y .
$y'-3y=0$

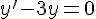
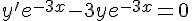
$y'e^{-3x}-3ye^{-3x}=0$

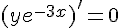
$(ye^{-3x} )'=0$

Il existe 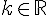$k\in\mathbb{R}$ tel que :

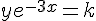
$ye^{-3x}=k$

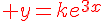
${\color{DarkRed} y=ke^{3x}}$

2. Déterminer la solution de (E) dont la courbe représentative passe par le point de coordonnées (2; 3).

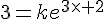
$3=ke^{3\times 2}$

$3=ke^{6}$

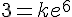
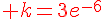
${\color{DarkRed} k=3e^{-6}}$

Conclusion : la solution est 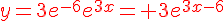$y=3e^{-6}e^{3x}={\color{DarkRed} 3e^{3x-6}}$

Exercice 7 :

1. L’équation différentielle donnée est 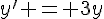$y' = 3y$ .

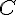C’est une équation différentielle du premier ordre à coefficients constants, homogène. On peut donc chercher une solution de la forme $y(t) = Ce^{rt}$ , avec $C$ et à déterminer.

En substituant cette forme dans l’équation différentielle, on a
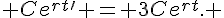
$Ce^{rt}' = 3Ce^{rt}.$
En dérivant le terme de gauche, on obtient
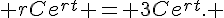
$rCe^{rt} = 3Ce^{rt}.$
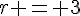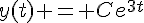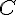Comme $Ce^{rt}$ est différent de zéro, on peut diviser des deux côtés par $Ce^{rt}$ , ce qui donne $r = 3$ . Ainsi, toutes les solutions de l’équation différentielle sont de la forme $y(t) = Ce^{3t}$ , où $C$ est une constante.

2. Pour déterminer la solution de l’équation différentielle (E) qui passe par le point 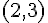$(2,3)$ , on utilise la condition initiale 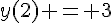$y(2) = 3$ . On a donc

3 = Ce^{3\cdot 2} = 9C,

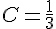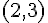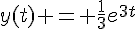ce qui donne $C=\frac{1}{3}$ . Ainsi, la solution de (E) qui passe par le point $(2,3)$ est donnée par $y(t) = \frac{1}{3}e^{3t}$ .

Exercice 8 :

1.Résoudre sur $\mathbb{R}$ chacune des équations différentielles suivantes :

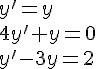
$y'=y\4y'+y=0\y'-3y=2$

2.On considère l’équation différentielle : 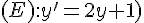$(E):y'=2y+1)$ .

Déterminer la solution de (E) sur $\mathbb{R}$ dont la courbe passe par le point A(0;3) dans un repère du plan.

Exercice 9 :

On considère l’équation différentielle 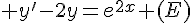$y'-2y=e^{2x} (E)$ .

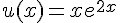1. Démontrer que la fonction u définie sur $\mathbb{R}$ par $u(x)=xe^{2x}$ est une solution de (E) .

2. Résoudre l’équation différentielle 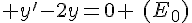$y'-2y=0 \,\,(E_0)$ .

3. Démontrer qu’une fonction v définie sur 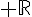$\mathbb{R}$ est solution de (E) si et seulement si v-u est solution de $(E_0)$ .

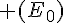4. En déduire toutes les solutions de l’équation (E) .

5. Déterminer la fonction, solution de (E), qui prend la valeur 1 en 0 .

6. Le plan est muni d’un repère orthonormé 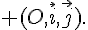$(O,\vec{i},\vec{j}).$

Soit la fonction f définie sur 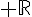$\mathbb{R}$ par $f(x)=(x+1)e^{2x}$ .

On note C la courbe représentative de f dans le repère 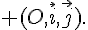$(O,\vec{i},\vec{j}).$

a. Etudier les variations de f puis dresser son tableau de variation .

b. Tracer C .

Exercice 10 :
On désigne par q(t) la température (exprimée en degré Celsius) d’un corps à l’instant t (exprimé en heure).

A l’instant t = 0 , ce corps dont la température est de 100 °C est placé dans une salle à 20 °C.

D’après la loi de refroidissement de Newton, la vitesse de refroidissement q ‘ (t) est
proportionnelle à la différence entre la température du corps et celle de la salle.

On suppose que le coefficient de refroidissement est – 2, 08 .

1. Justifier que q ‘ (t) = – 2 , 08q(t) + 41,6 .

q ‘ (t) est proportionnelle à la différence entre la température du corps et celle de la salle.

Il existe 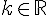$k\in\mathbb{R}$ tel que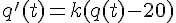 $q'(t)=k(q(t)-20)$

or le coefficient de proportionnalité k correspond au coefficient de refroidissement.

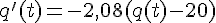
$q'(t)=-2,08(q(t)-20)$

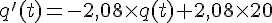
$q'(t)=-2,08\times q(t)+2,08\times 20$

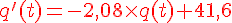
${\color{DarkRed} q'(t)=-2,08\times q(t)+41,6}$

2. En déduire l’expression de q(t) .

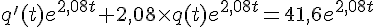
$q'(t)e^{2,08t}+2,08\times q(t)e^{2,08t}=41,6e^{2,08t}$

$[q(t)e^{2,08t} ]'=41,6e^{2,08t}$

$[q(t)e^{2,08t} ]'= [\frac{41,6}{2,08}e^{2,08t} ]'$

Deux dérivées sont égales si et seulement si les fonctions sont égales à une constante près.

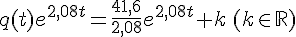
$q(t)e^{2,08t} =\frac{41,6}{2,08}e^{2,08t}+k\,(k\in\mathbb{R})$

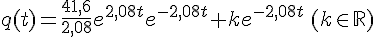
$q(t) =\frac{41,6}{2,08}e^{2,08t}e^{-2,08t} +ke^{-2,08t} \,(k\in\mathbb{R})$

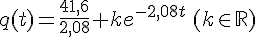$q(t) =\frac{41,6}{2,08} +ke^{-2,08t} \,(k\in\mathbb{R})$ or q(0)=100

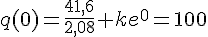
$q(0) =\frac{41,6}{2,08} +ke^{0}=100$
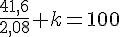
$\frac{41,6}{2,08} +k =100$

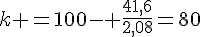
$k =100- \frac{41,6}{2,08}=80$

Conclusion : 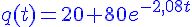${\color{DarkBlue} q(t) =20+80e^{-2,08t} }$

3. Déterminer le sens de variation de la fonction q sur 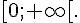$[0;+\infty[.$
q est strictement décroissante, la température va décroître.

4. Calculer la limite de q en $+\infty.$
Interpréter ce résultat.

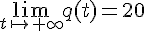$\lim_{t\mapsto +\infty}q(t)=20$ la température du corps va se stabiliser et prendre la température initiale de la salle.

4.4/5 - (26013 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les équations différentielles : corrigé des exercices de maths en terminale en PDF.» au format PDF.

Ressources de terminale

D'autres cours et exercices à consulter

Logarithme népérien : corrigé des exercices de maths en terminale en PDF.

Probabilités : corrigé des exercices de maths en 1ère.

Probabilités : corrigé des exercices de maths en terminale en PDF.

Barycentre : corrigé des exercices de maths en terminale en PDF.

Calcul intégral : corrigé des exercices de maths en terminale en PDF.

Dérivée d’une fonction : corrigé des exercices de maths en terminale en PDF.

Nombres complexes : corrigés des exercices de maths en terminale en PDF.

Produit scalaire : corrigé des exercices de maths en terminale en PDF.

Exercices de maths interactifs avec saisie au clavier des réponses.

Maths et programmation dans un escape game.

Exercices de maths avec des patterns pour travailler les automatismes.

SCRATCH Dimension ; exercices de maths et de programmation avec scratch.

Exercices de géométrie sous forme d'escape game.

Calculus Arcana : escape game de calcul littéral.

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Les équations différentielles : corrigé des exercices de maths en terminale en PDF.

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

D'autres cours et exercices à consulter

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques