Dérivée d’une fonction numérique : corrigé des exercices en 1ère en PDF.
Mis à jour le 15 septembre 2025
Exercice 1 :
Dériver la fonction f dans les cas suivants :
1. 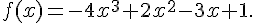
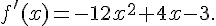
2. 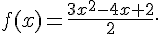
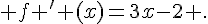
3. 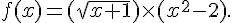
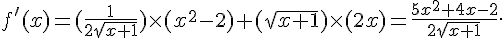
4. 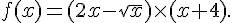
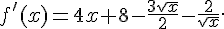
5. 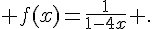
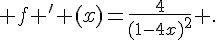
6. 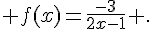
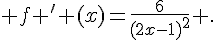
7. 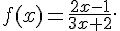

8. 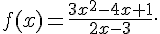
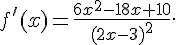
9. 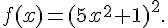
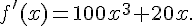
10. 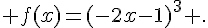
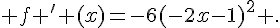
11. 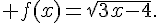
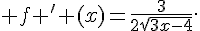
12. 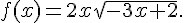
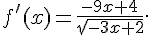
Exercice 2 :
1. 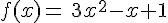 avec
avec 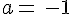 .
.

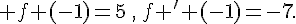
donc l’équation de la tangente en a=-1 est :
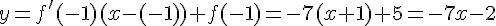
2. 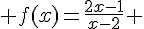 avec a= 3.
avec a= 3.
Montrer que : f ‘ (3)=-2 ; f(3) = 5 et y = -2x+11.
3. 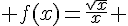 avec a= 9.
avec a= 9.
Montrer que : 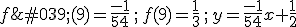
Exercice 3 :
Soit f la fonction définie sur 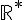 par :
par :
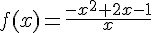 .
.
On note C sa courbe représentative dans un repère orthonormé.
1. Déterminer les abscisses des points de la courbe C où la tangente est horizontale .
Le coefficient directeur de la tangente est donc nul or il vaut 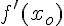 .
.
Résolvons 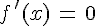
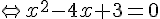
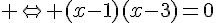
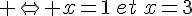
2. Existe-t-il des points de la courbe C où la tangente admet un coefficient directeur égal à – 2 ?
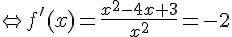
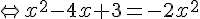
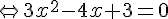
Il n’y a donc aucun point de la courbe.
3. Déterminer les abscisses des points de la courbe C où la tangente est parallèle à la droite d’équation 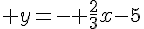 .
.
Si elle est parallèle cela équivaut à dire qu’elle a le même coefficient directeur,
nous sommes donc amenés à résoudre l’équation :
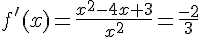
Il n’existe aucun point.
Exercice 4 :
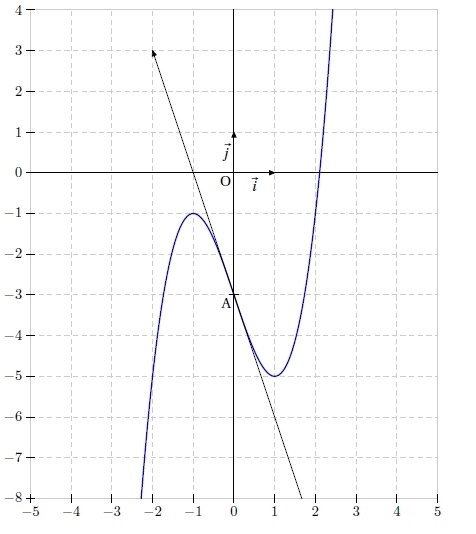
Soit f la fonction définie sur R par 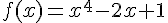 .
.
Soit (Cf ) sa courbe représentative.
1. Donner, en justifiant, l’équation de la tangente (T) à la courbe (Cf ) au point A d’abscisse 0.
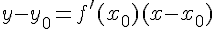
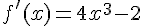
 et
et 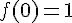
donc
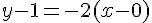
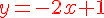
2. Tracer dans un même repère la courbe (Cf ) et la tangente (T) sur l’intervalle [- 1 ; 1,5].
Exercice 5 :
Le but de cet exercice est de calculer la limite suivante :
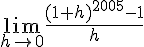 .
.
Pour cela on considère la fonction  définie sur
définie sur  par
par 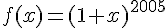 .
.
1. Calculer la dérivée f’ de la fonction f. Calculer f ‘ (0).
f est un polynôme donc dérivable sur  .
.
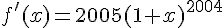
et 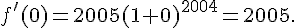
2. Calculer l’accroissement moyen de la fonction f entre 0 et h. En déduire la limite ci-dessus.
L’accroissement moyen de f entre o et h est :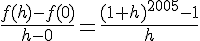
et 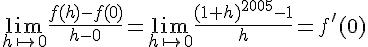 car la fonction f est dérivable en 0.
car la fonction f est dérivable en 0.
Conclusion : 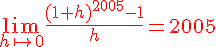
Exercice 6 :
1. Soit t la durée du trajet en heure. Exprimer t en fonction de la vitesse 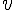 .
.

2. Calculer le prix de revient P(v) du trajet en fonction de v.
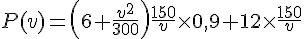
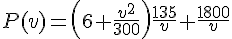
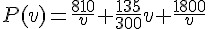
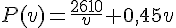
3. Quel doit être la vitesse v du camion pour que le prix de revient P(v) de la course soit minimal ?

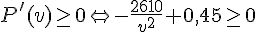
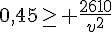
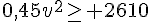
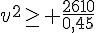
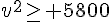
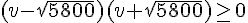
ceci est vérifié pour 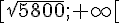
Donc le minimum est atteint pour 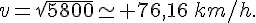
Conclusion : pour que le prix de revient de la course soit minimal, il faut que le camion roule à une vitesse moyenne de 76,16 km/h.
Exercice 7 :
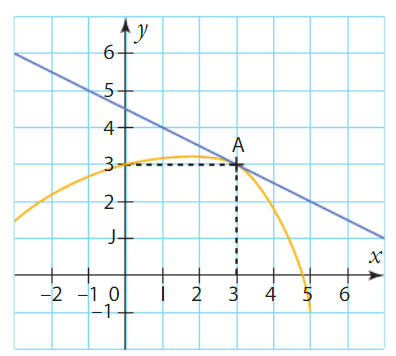
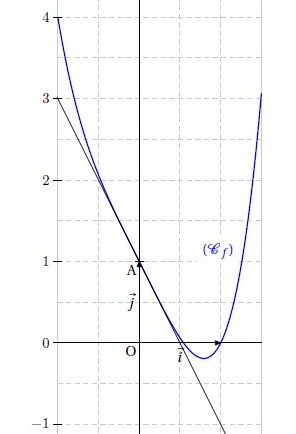
Soit (P) la parabole définie par la fonction  .
.
Calculer les coordonnées de son sommet S.
Son sommet est le minimum donc la dérivée est nulle en ce point.
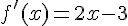
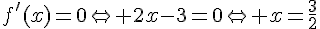
et
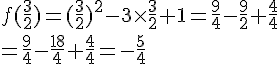
Les coordonnées de son sommet sont 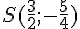
Exercice 8 :
On considère un rectangle dont le périmètre P est égal à 4 cm.
1. Déterminer ses dimensions (longueur L et largeur l) sachant que son aire S est égale à 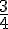 cm².
cm².
Nous avons :
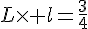 et
et 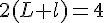 soit
soit 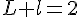
Nous avons la somme et le produit de deux nombres, ils sont solution de l’équation :
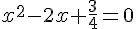
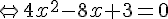
Calculons le discriminant :
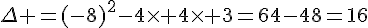
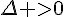 il y a donc deux racines réelles distinctes.
il y a donc deux racines réelles distinctes.
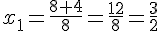 et
et 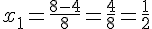
Conclusion : la longueur est 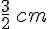 et la largeur est
et la largeur est 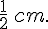
2. On recherche maintenant les dimensions du rectangle de façon que son aire S soit maximale.
a. Exprimer S en fonction de la largeur l.
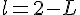
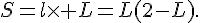
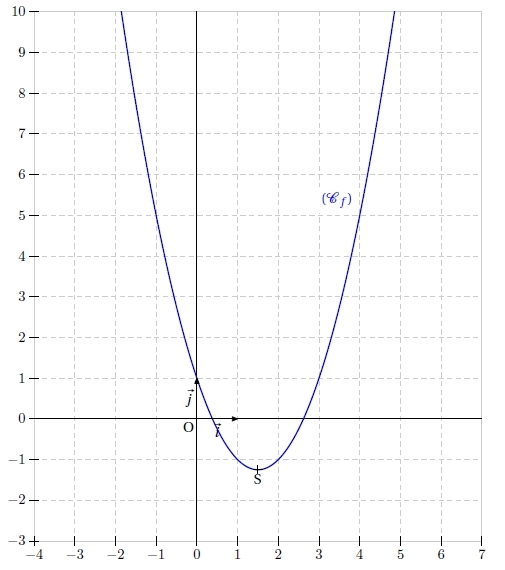
b. On considère la fonction f définie sur  par
par 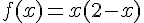 .
.
Cette fonction f correspond à l’aire du rectangle.
Calculer la dérivée f ‘ de f puis étudier son signe.
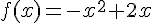
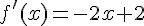
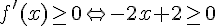
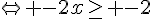
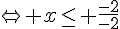
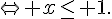
Dresser le tableau de variations de la fonction f.
f est croissante sur [0;1] et décroissante sur [1;2].
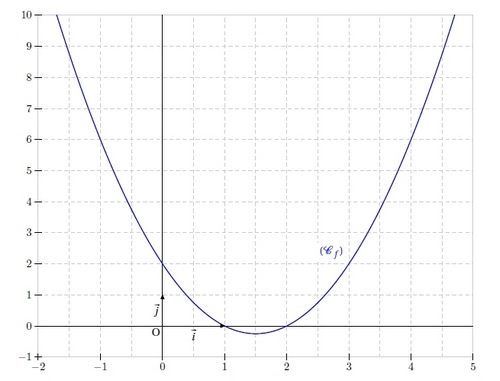
Tracer la représentation graphique (Cf ) de la fonction f sur [0 ; 2].
c. En déduire les dimensions du rectangle dont le périmètre P est égal à 4 m et l’aire S est maximale.
Pour que S soit maximale il faut que L = 1 cm.
et donc la largeur est l = 2-1=1 cm
Finalement ce rectangle est un carré de côté 1 cm.
Exercice 9 :
On considère la fonction f définie sur R par : 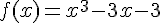 .
.
On note (Cf ) sa représentation graphique.
1.Calculer la dérivée f ‘ de f puis étudier son signe.
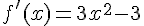
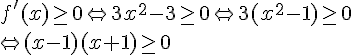
donc f’ est négative sur [ – 1 ; 1 ] .
2. Dresser le tableau de variations de la fonction f.
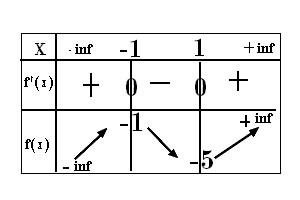
3. Déterminer une équation de la tangente (T) à (Cf ) au point d’abscisse 0.
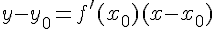
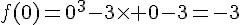
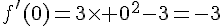
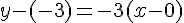
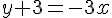

4. Tracer (T) et (Cf ) dans un même repère.
5. Démontrer que l’équation f(x) = 0 admet une solution unique  dans l’intervalle [2 ; 3].
dans l’intervalle [2 ; 3].
f est continue et strictement croissante sur [2;3], de plus elle passe d’une valeur négative à une valeur positive
donc d’après le théorème de bijection 0 admet un unique antécédent sur [2 ; 3 ].
6. Donner une valeur approchée de  , par défaut, à
, par défaut, à 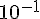 près.
près.
Exercice 10 :
1. Dresser le tableau de variations de la fonction f définie sur R par : 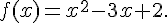
Nous avons 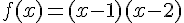
f est décroissante sur ![]-\infty;1,5]](https://mathovore.fr/latex-images/4f714d3e4fefa4282b2c3b37909a98c9.png) et croissante sur
et croissante sur 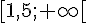 .
.
2. Résoudre l’équation f(x) = 0.
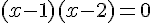
C’est une équation produit, il y a deux solutions : 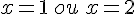 .
.
Exercice 11 :
1. Calculer la dérivée f ‘ de f.
f est un polynôme donc dérivable sur 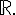
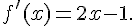
2. Déterminer une équation de la tangente (T) à la courbe (Cf ) au point d’abscisse 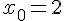 .
.
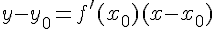
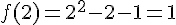
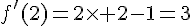


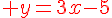
3. Résoudre par le calcul l’équation g(x) = f(x).


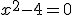
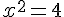

Il y a donc deux points d’intersection entre ces deux courbes.
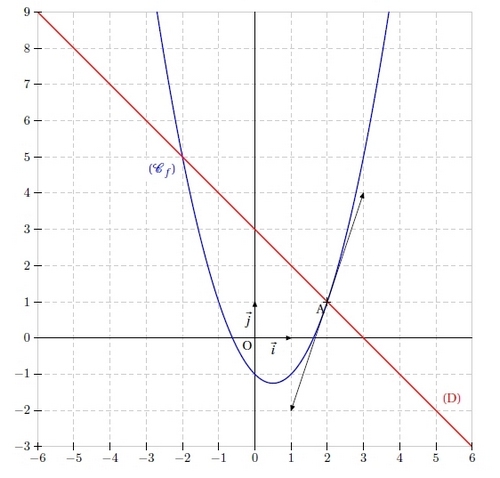
4. Préciser les coordonnées des points d’intersections de (Cf ) et (D).
f(2)= 1 donc le premier point d’intersection est I(2;1).
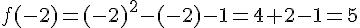
le second point d’intersection est J ( – 2 ; 5 ) .
5. Tracer sur un même repère les droites (T), (D) et la courbe (Cf ).
Exercice 12 :
Dériver les fonctions suivantes :
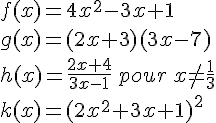
f est une fonction polynôme dérivable sur 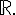
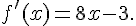
g est le produit de deux fonctions dérivables sur  .
.
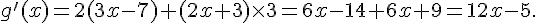
h est une fonction rationnelle dérivable sur 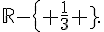
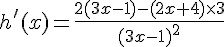
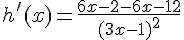

Exercice 13 :
Dériver les fonctions suivantes :
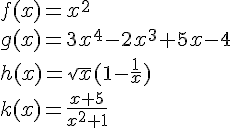
f est un polynôme donc dérivable sur  .
.
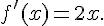
g est un polynôme donc dérivable sur  .
.
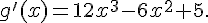
h est un produit de fonctions dérivables sur 

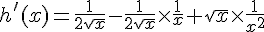
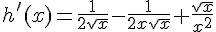
k est une fonction rationnelle dérivable sur 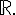

Exercice 14 :
Soit  une fonction définie sur
une fonction définie sur  par
par 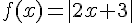 .
.
Etudier la dérivabilité de  sur
sur  .
.
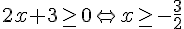
Premier cas :

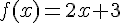 et f est dérivable sur
et f est dérivable sur ![]-\frac{3}{2};+\infty [](https://mathovore.fr/latex-images/13573998acf18fde9f83644908c6472b.png) en tant que fonction affine .
en tant que fonction affine .
et 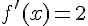 .
.
Second cas :
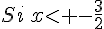
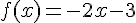 et f est dérivable sur
et f est dérivable sur ![]-\infty;-\frac{3}{2} [](https://mathovore.fr/latex-images/d33abc55c3f41215e2f580f77b3cfb30.png) en tant que fonction affine .
en tant que fonction affine .
et 
Dérivabilité en 0 :
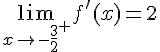 et
et 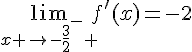
Conclusion : f est dérivable sur 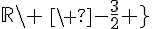
Exercice 15 :
Démontrez que si u est une fonction dérivable sur un intervalle I, alors:
a) u 2 est dérivable sur I et (u2 )’=2uu’.
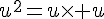
Or si u est dérivable, un produit de fonctions est aussi dérivables sur l’intervalle I.
En utilisant la formule de la dérivée d’un produit, nous obtenons :
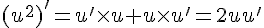
b) u3 est dérivable sur I et (u3 )’=3u2 u’.
de même :

les fonctions 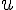 et
et 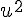 sont dérivables sur I donc
sont dérivables sur I donc 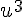 également
également
en tant que produit de fonctions dérivables sur I .
Et en réutilisant la formule de la dérivée d’un produit :

En utilisant la question a) :

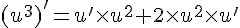
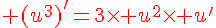
Exercice 16 :
1. f est dérivable sur  car c’est un polynôme .
car c’est un polynôme .
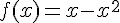
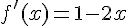
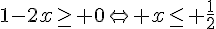
donc f est croissante sur ![]-\infty; \frac{1}{2}]](https://mathovore.fr/latex-images/20629f8e375e4d0d1b6b6facd8cafd3d.png) et décroissante sur
et décroissante sur 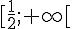 .
.
donc son maximum est atteint en 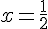 .
.

donc 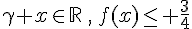 .
.
3. 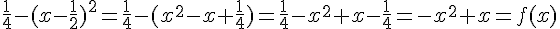
Exercice 17 :
Soit la fonction 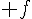 définie sur
définie sur 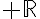 par
par 
1. 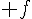 sur
sur 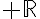 en tant que fonction polynômiale.
en tant que fonction polynômiale.
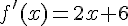
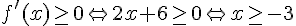
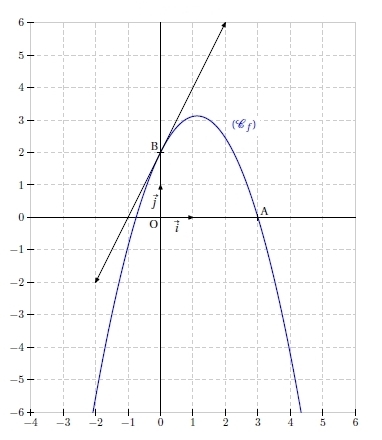
donc f est croissante sur 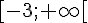 et décroissante sur
et décroissante sur ![]-\infty;3]](https://mathovore.fr/latex-images/970ee4456f26e8fe0e1ba0adef6a1a2e.png)
2. Résolvons l’équation : .
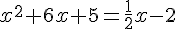
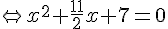
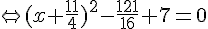
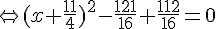
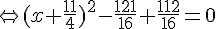
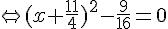
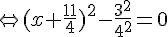
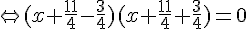
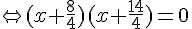
Or un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
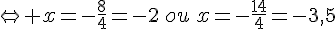
de plus les ordonnées des points d’intersection vérifient :
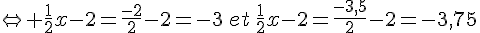
Donc les deux courbes se coupent aux points A(-2;-3) et B(-3,5;-3,75).
Exercice 18 :
Etudier les variations sur  de la fonction f définie par
de la fonction f définie par 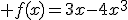 .
.
f est une fonction polynômiale donc dérivable sur  .
.
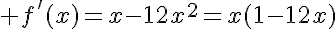
avec un tableau des signes, nous montrons que f’ est positive ou nulle sur ![[0;\frac{1}{12}]](https://mathovore.fr/latex-images/6e890eae79ec90d63fa4dceb950ad817.png)
donc f est croissante sur ![[0;\frac{1}{12}]](https://mathovore.fr/latex-images/6e890eae79ec90d63fa4dceb950ad817.png)
Exercice 19 :
Soit f la fonction définie sur  par :
par :
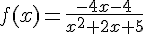 .
.
1. f est définie et dérivable sur  en tant que fonction rationnelle.
en tant que fonction rationnelle.
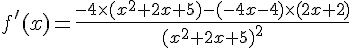
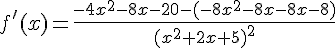
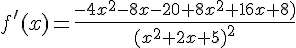
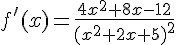
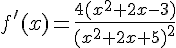
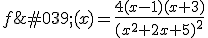
En effectuant un tableau des signes, nous obtenons :
f ‘ négative ou nulle sur ![[-3;1]](https://mathovore.fr/latex-images/cc5834a0c14f62ead1ef90714341e01a.png) donc f est décroissante sur
donc f est décroissante sur ![[-3;1]](https://mathovore.fr/latex-images/cc5834a0c14f62ead1ef90714341e01a.png) .
.
2. Déterminer les coordonnées du point A, intersection entre la courbe représentative de f et l’axe des abscisses .
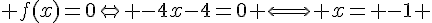
Donc les coordonnées du point A(-1;0) .
3.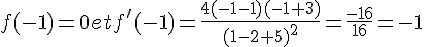
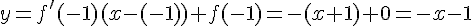
L’équation de la tangente en A à la courbe de f est y = – x – 1 .
Exercice 20 :
Etudier les variations sur ]-2 ; 1[ de la fonction 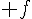 définie par :
définie par :
 .
.
C’est le même principe que précédemment
Montrer que f est croissante sur ![[0;\frac{28}{9}]\,donc\,sur\,[0;1[](https://mathovore.fr/latex-images/c4846bf7eab0f39334bfffd396c8e163.png)
Exercice 21 :
Soit  la fonction définie sur
la fonction définie sur  par
par 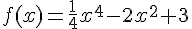
On appelle  sa représentation graphique dans un repère orthonormal.
sa représentation graphique dans un repère orthonormal.
1)a) Etudier la parité de  . Que peut-on en déduire pour
. Que peut-on en déduire pour  ?
?
f(-x)=f(x) donc la courbe de f est symétrique par rapport à l’axe des ordonnées.
b) Déterminer l’expression de la fonction dérivée de  et en déduire le tableau de variation de
et en déduire le tableau de variation de 
2) a) Déterminer une équation de la tangente à  au point d’abscisse 1.
au point d’abscisse 1.
b) Cette tangente recoupe  en deux autres points.
en deux autres points.
b.1) Montrez que les abscisses de ces points sont les solutions de l’équation :
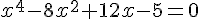
b.2) Vérifiez que l’on a :
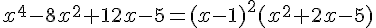
b.3) En déduire les abscisses de ces points.
Exercice 22 :
Soit (P) la parabole d’équation 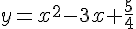
et (H) l’hyperbole d’équation  .
.
Le plan est ramené à un repère orthonormal.
1) Montrer que (P) et (H) rencontrent l’axe (Oy) en un même point A.
Indication : remplacer x par 0.
2) Montrer que les tangentes en A aux courbes (P) et (H) sont perpendiculaires.
indication : utiliser l’équation d’une tangente 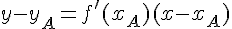
Rappel : Dans un repère orthonormé du plan, deux droites sont perpendiculaires si et seulement si le produit de leur coefficient directeur est égal à –1 .
Exercice 23 :
Indication : utiliser le fait qu’une équation réduite de la tangente en a est y-f(a)=f ‘ (a)(x-a)
Déterminer le réel m pour que la courbe d’équation 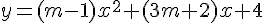
admette au point d’abscisse –1 une tangente de coefficient directeur 6.
Exercice 24 :
Indication : utiliser le fait qu’une équation réduite de la tangente en a est :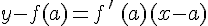 .
.
Soit la fonction 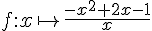 définie sur
définie sur 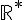 et soit (C) sa courbe représentative.
et soit (C) sa courbe représentative.
Déterminer les abscisses des points de (C) où la tangente :
1) est horizontale
2) est parallèle à la droite d’équation 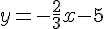 .
.
Exercice 25 :
Une parabole 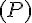 admet dans un repère
admet dans un repère 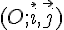 une équation du type :
une équation du type :
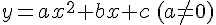 .
.
1. Déterminer les coefficients a, b et c sachant que 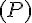 coupe l’axe des abscisses au point A d’abscisse 3, l’axe des ordonnées au point B d’ordonnée 2 et qu’elle admet en ce point la droite d’équation y = 2x + 2 pour tangente.
coupe l’axe des abscisses au point A d’abscisse 3, l’axe des ordonnées au point B d’ordonnée 2 et qu’elle admet en ce point la droite d’équation y = 2x + 2 pour tangente.
Nous avons :
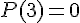
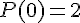
et le coefficient directeur de la tangente étant le nombre dérivé : 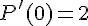
Nous obtenons le système suivant :
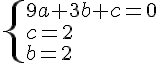
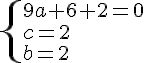
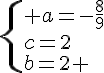
Conclusion : 
2. Indiquer l’abscisse du second point d’intersection de 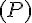 avec (Ox).
avec (Ox).
Résolvons l’équation P(x)=0
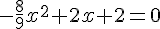 (multiplions par -9)
(multiplions par -9)
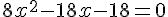
Calculons la valeur du discriminant :
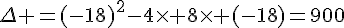
Le discriminant étant strictement positif, il existe deux racines réelles distinctes.
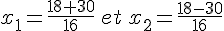
Exercice 26 :
Indications :
1. 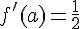
2.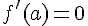
3.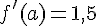
4.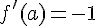
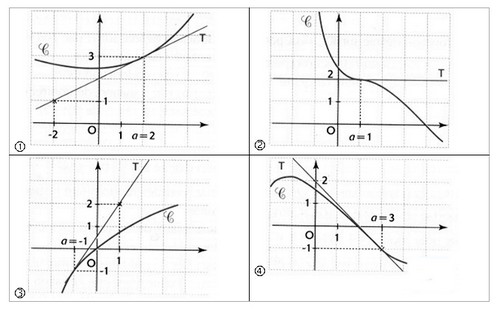
(C) représenter une fonction dérivable sur  et la droite T est tangente à (C) au point d’abscisse a.
et la droite T est tangente à (C) au point d’abscisse a.
Dans chaque cas détermine f’(a) et donner une équation de la tangente T.
Exercice 27 :
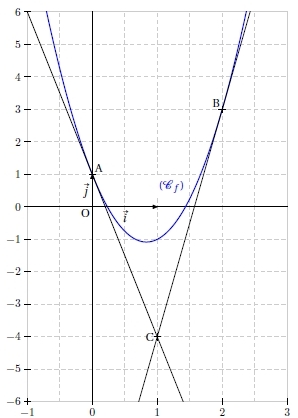
On considère la fonction f définie par :
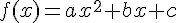
dont la parabole (Cf ) passe par les points A (0 ; 1) et B (2 ; 3).
Les tangentes en A et B se coupent au point C (1 ; – 4).
1. Déterminer une équation des tangentes à (Cf ).
Pour la tangente en A :
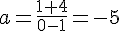
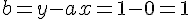
donc
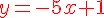
Pour la tangente en B :
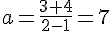
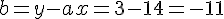
donc
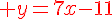
En déduire f ‘ (0) et f ‘ (2).
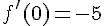 et
et 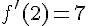
2. Exprimer f ‘ (x) en fonction de a, b et c.
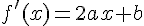
3. A l’aide des valeurs de f ‘ (0), f ‘ (2) et f(0), trouver trois équations vérifiées par a, b et c puis déterminer l’expression algébrique de la fonction f.
Nous obtenons :
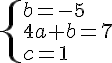

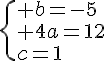

Conclusion :
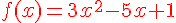
Exercice 28 :
On considère la fonction  définie sur
définie sur par
par 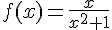 .
.
1. Calculer les limites de f en  et en
et en 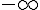 .
.
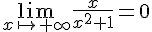 et
et 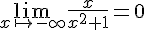
2. Calculer la dérivée f » de f et étudier son signe.
f est est deux fois dérivable sur son domaine de définition en tant que fonction rationnelle.

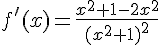
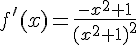
et
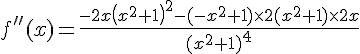
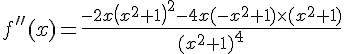
![f''(x)=\frac{(x^2+1)[-2x(x^2+1)-4x(-x^2+1)] }{(x^2+1)^4}](https://mathovore.fr/latex-images/48525d030b3f9a9d861e93f446f95389.png)
![f''(x)=\frac{(x^2+1)[-2x^3-2x+4x^3-4x] }{(x^2+1)^4}](https://mathovore.fr/latex-images/341fe9add98c1244e6ec738bc5f2058b.png)
![f''(x)=\frac{(x^2+1)[2x^3-6x] }{(x^2+1)^4}](https://mathovore.fr/latex-images/1a170d135f14a2f5c7461932e76ec613.png)
![f''(x)=\frac{2x(x^2+1)[x^2-3] }{(x^2+1)^4}](https://mathovore.fr/latex-images/c328c0e1e984ef3d7d7c976cd7711aa1.png)
donc le signe de f » est celui de 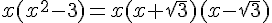
En établissant un tableau des signes,
nous obtenons que f » est positive sur ![[-\sqrt{3};0]\cup [\sqrt{3};+\infty[](https://mathovore.fr/latex-images/8c5d34879f6aecc9ede7590d6015b8cb.png)
donc f ‘ est croissante sur ![[-\sqrt{3};0]\cup [\sqrt{3};+\infty[](https://mathovore.fr/latex-images/8c5d34879f6aecc9ede7590d6015b8cb.png)
3. Dresser le tableau de variation de la fonction f.
f est croissante sur [-1;1]
Exercice 29 :
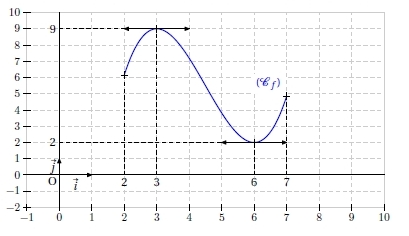
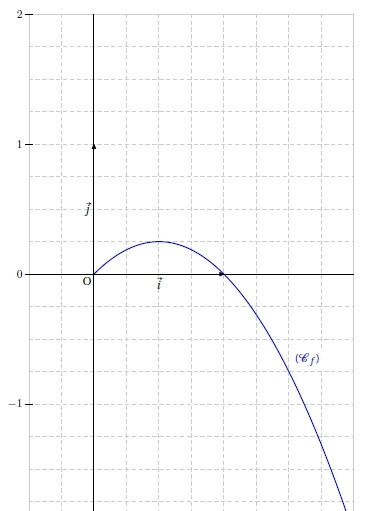
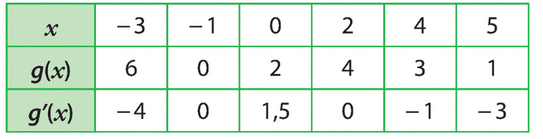
Ci-dessous est donnée la courbe (Cf ) représentant une fonction f définie et dérivable sur l’intervalle [2 ; 7].
1. Par lecture graphique, donner sans justifier la valeur de :
f(3) ; f ‘ (3) ; f(6) ; f ‘ (6).
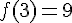
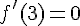
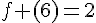
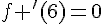
2. Le graphique ne permet pas la lecture de f ‘ (4).
Préciser néanmoins son signe. Expliquer.
Exercice 30 :
Soit  la fonction définie sur
la fonction définie sur  par
par 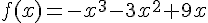 .
.
1. Calculer la dérivée 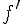 et étudier son signe.
et étudier son signe.
f est un polynôme donc dérivable sur  .
.
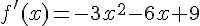
2. Dresser le tableau de variations de la fonction f.
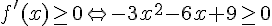
Calculons la valeur du discriminant :
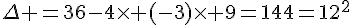
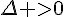 , il y a donc deux racines réelles distinctes.
, il y a donc deux racines réelles distinctes.
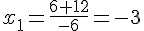 et
et 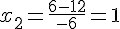
Conclusion : 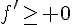 sur
sur ![[-3;1]](https://mathovore.fr/latex-images/cc5834a0c14f62ead1ef90714341e01a.png)
donc f est croissante sur ![[-3;1]](https://mathovore.fr/latex-images/cc5834a0c14f62ead1ef90714341e01a.png) .
.
Exercice 31 :
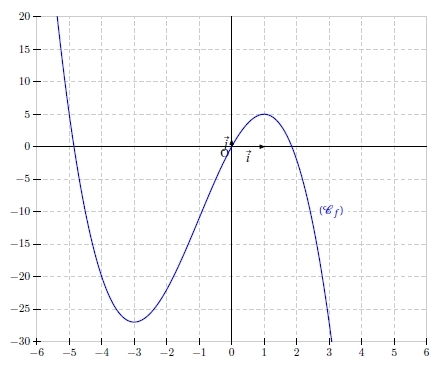
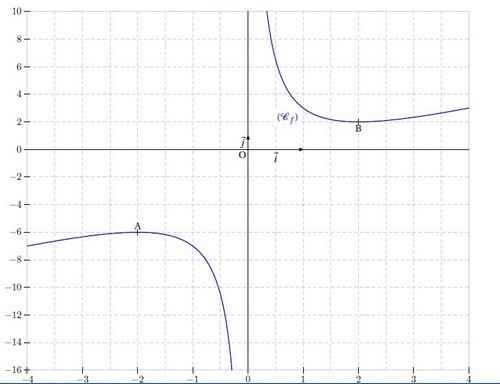
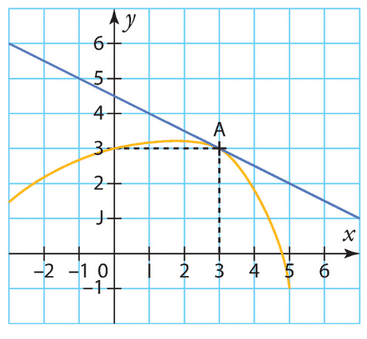
Sur le graphique ci-dessous sont représentées la courbe (Cf ) de la fonction f définie sur par :
par :
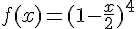 ainsi que la tangente (T) à (Cf ) au point d’abscisse
ainsi que la tangente (T) à (Cf ) au point d’abscisse 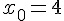 .
.
1. Donner, par lecture graphique, et sans justifications, la valeur du nombre f ‘ (4).
C’est la valeur du coefficient directeur de la tangente en 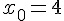
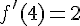
2. Déterminer, à l’aide du calcul de la dérivée de f, la valeur du nombre f ‘ (3).
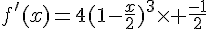
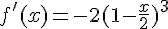

Exercice 32 :
Soit  la fonction définie sur
la fonction définie sur 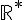 par
par 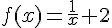 .
.
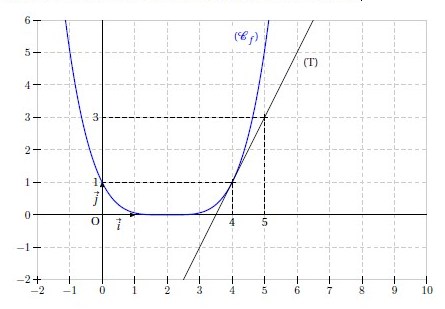
1. Montrer que f est dérivable en 2.
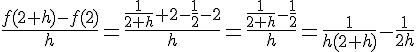
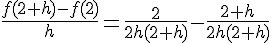

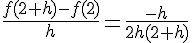
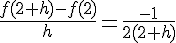
La limite lorsque h tend vers 0 existe donc f est dérivable en 2 et :
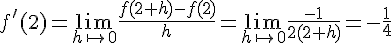
2. Déterminer une équation de la tangente (T) à la courbe (Cf ) représentant f au point d’abscisse 2.
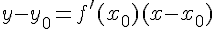
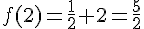
ainsi 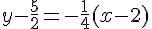
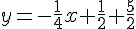
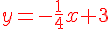
Exercice 33 :
1. Dériver les fonctions f et g définies ci-dessous :
![f(x)=\frac{x}{x+\sqrt{x}}\,sur\,]0;+\infty[](https://mathovore.fr/latex-images/718eba8e7d1288ffcd7bacff697ddc63.png)
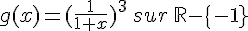
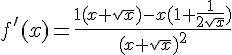
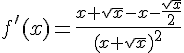

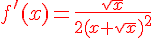
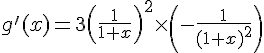
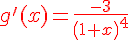
2. Calculer f ‘ (16) et g ‘ (2).

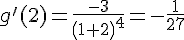
Exercice 34 :
Indication : vérifiez vos résultats sur la courbe ci-dessous.
1. Etudier le sens de variation de la fonction  définie sur
définie sur  par :
par :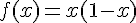 .
.
2. En déduire un encadrement de f(x) sur [0 ; 2].
Exercice 35 :
On considère la fonction  définie sur
définie sur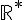 par
par 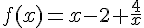 .
.
1. Calculer la dérivée f ‘ et étudier son signe.
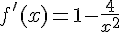
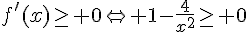
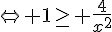
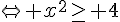
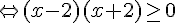
On en déduit que f est décroissante sur [ -2 ; 2 ].
2. Dresser le tableau de variations de la fonction f.
3. Tracer la représentation graphique (Cf ) de la fonction f sur![[-4 ; 0[\cup ]0 ; 4]](https://mathovore.fr/latex-images/17e5369aeae1538309d517e2d32f24cb.png) .
.
EXERCICE 36 :
a) La fonction f est définie sur l’ensemble des nombres réels, donc elle est dérivable sur  .
.
Sa dérivée est 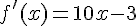 .
.
b) La fonction g est définie sur l’ensemble des nombres réels non nuls, donc elle est dérivable sur 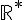 . Sa dérivée est
. Sa dérivée est 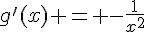 .
.
c) La fonction h est définie sur l’intervalle 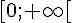 , donc elle est dérivable sur cet intervalle.
, donc elle est dérivable sur cet intervalle.
Sa dérivée est 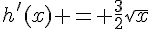 .
.
d) La fonction j est définie sur 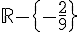 , donc elle est dérivable sur cet ensemble. Sa dérivée est
, donc elle est dérivable sur cet ensemble. Sa dérivée est 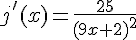 .
.
EXERCICE 37 :
La fonction g est définie sur l’ensemble des nombres réels, donc elle est dérivable sur  .
.
Sa dérivée est 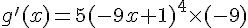 .
.
Simplifiée, on obtient 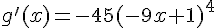 .
.
EXERCICE 38 :
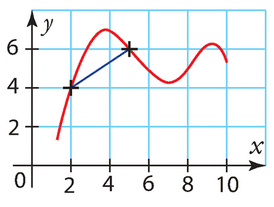
Le taux de variation de f entre 2 et 5 est donné par la formule 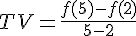 .
.
D’après le graphique, on a 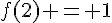 et
et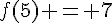 .
.
Donc, le taux de variation de f entre 2 et 5 est 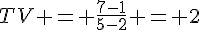 .
.
EXERCICE 39 :
La droite passant par 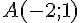 et
et 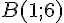 a pour coefficient directeur
a pour coefficient directeur 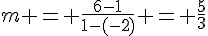 . Comme la droite est tangente à la courbe en A, on a
. Comme la droite est tangente à la courbe en A, on a 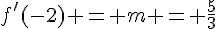 .
.
EXERCICE 40 :
1. On a 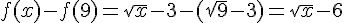 et
et 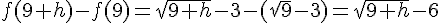 .
.
En utilisant l’identité remarquable 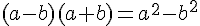 , on peut écrire :
, on peut écrire :
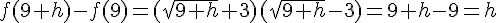
Le taux de variation de f entre 9 et 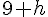 est donc
est donc 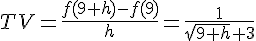 .
.
2. Comme la limite de cette expression quand h tend vers 0 est finie, la fonction f est dérivable en 9 et sa dérivée est 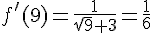 .
.
EXERCICE 41 :
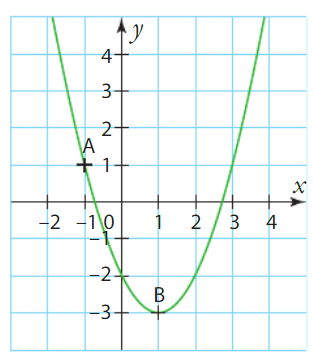
On a g(3) = 6 (coordonnée y du point B).
Comme la tangente en A a pour coefficient directeur  , on peut écrire :
, on peut écrire : 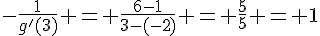 .
.
Donc, g'(3) = -1.
EXERCICE 42 :
a) On peut écrire 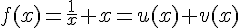 avec
avec 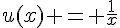 et
et 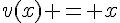 .
.
Les fonctions u et v sont dérivables sur 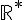 et sur
et sur  , respectivement.
, respectivement.
La fonction somme est dérivable sur 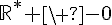 et sa dérivée est
et sa dérivée est 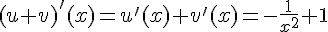 .
.
b) On peut écrire 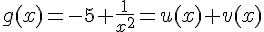 avec
avec 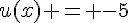 et
et  .
.
Les fonctions u et v sont dérivables sur  et sur
et sur 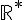 , respectivement.
, respectivement.
La fonction somme est dérivable sur 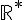 et sa dérivée est
et sa dérivée est 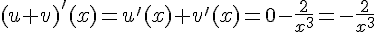 .
.
c) On peut écrire 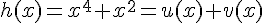 avec
avec 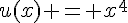 et
et 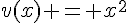 .
.
Les fonctions u et v sont dérivables sur  et la fonction somme est dérivable sur
et la fonction somme est dérivable sur  avec
avec 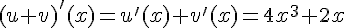 .
.
EXERCICE 43 :
1. L’équation de la courbe représentative de f est « 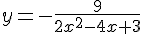 ».
».
2. Nous plaçons un point sur la courbe en  .
.
3. Nous traçons la tangente à la courbe en ce point.
4. Le coefficient directeur de la tangente est environ 11.
5. En plaçant le point sur les différentes valeurs de x données dans le tableau de valeurs et en traçant les tangentes, on peut estimer les valeurs approchées des dérivées demandées : 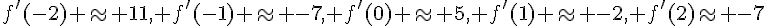 .
.
EXERCICE 44 :
1. Les points sont 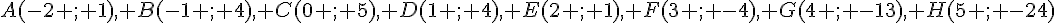 .
.
2. En chacun de ces points, on trace la tangente à la courbe 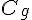 .
.
3. Une allure possible de 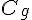 est représentée ci-dessous :
est représentée ci-dessous :
Courbe à créer….
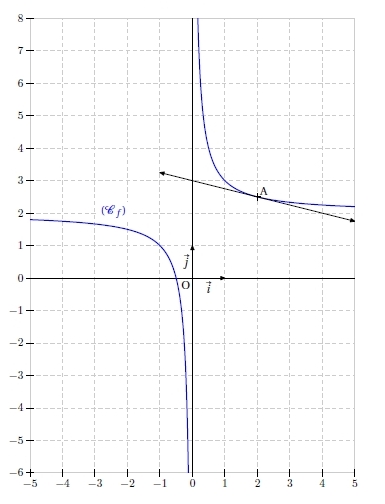
EXERCICE 45 :
Le coefficient directeur de la tangente à 6 (c’est-à-dire au point d’abscisse 2) est la valeur de la dérivée f'(2). En lisant sur le graphique, on a  . Donc le coefficient directeur de la tangente à 6 est environ -2.
. Donc le coefficient directeur de la tangente à 6 est environ -2.
EXERCICE 46 :
a) La fonction f est définie pour tout x sauf 0. Donc, f est dérivable sur 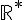 et sa dérivée est
et sa dérivée est 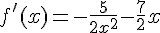 .
.
b) La fonction g est définie pour tout x sauf 0. Donc, g est dérivable sur 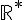 et sa dérivée est
et sa dérivée est 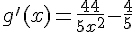 .
.
c) La fonction h est définie pour tout x sauf 3. Donc, h est dérivable sur 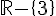 et sa dérivée est
et sa dérivée est 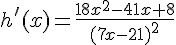 .
.
d) La fonction j est définie pour tout x sauf 0. Donc, j est dérivable sur 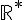 et sa dérivée est
et sa dérivée est 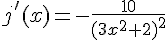 .
.
e) La fonction k est définie sur l’intervalle ]-∞;1[ ∪ ]1;+∞[ car le dénominateur 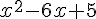 s’annule en
s’annule en 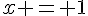 .
.
On peut factoriser 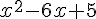 en
en 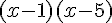 , donc la fonction est dérivable sur cet intervalle. Sa dérivée est
, donc la fonction est dérivable sur cet intervalle. Sa dérivée est 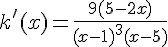 .
.
f) La fonction m est définie pour tout x tel que 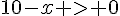 , c’est-à-dire sur
, c’est-à-dire sur ![]-\infty ; 10]](https://mathovore.fr/latex-images/52f528639754e09ed0941f44b385c45b.png) .
.
Donc, m est dérivable sur cet intervalle et sa dérivée est 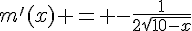 .
.
EXERCICE 47 :
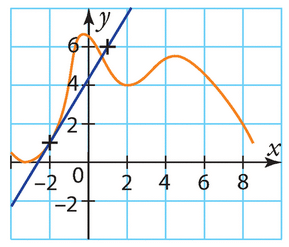
Le taux de variation de f entre -1 et 1 est donné par la formule 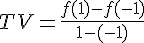 .
.
D’après le graphique, on a f(-1) ≈ -6 et 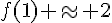 .
.
Donc, le taux de variation de f entre -1 et 1 est 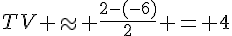 .
.
EXERCICE 48 :
On peut écrire l’égalité sous la forme :  .
.
En simplifiant, on obtient :  .
.
Donc, le taux de variation de f entre  et
et 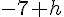 est TV = 9.
est TV = 9.
Comme ce taux ne dépend pas de h, on peut dire que la fonction f est dérivable en -7 et que 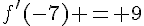 .
.
EXERCICE 49 :
En faisant tendre x vers 3 dans l’équation 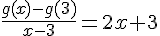 , on trouve
, on trouve  ,
,
donc 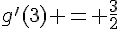 .
.
Donc la fonction g est dérivable en 3 et 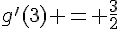 .
.
EXERCICE 50 :
On a g(3) = 6 (coordonnée y du point B).
Comme la tangente en A a pour coefficient directeur  , on peut écrire :
, on peut écrire : 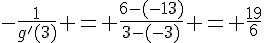 .
.
Donc, 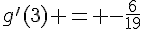 .
.
EXERCICE 51 :
La courbe représentative  est reproduite ci-dessous :
est reproduite ci-dessous :
Tracer la courbe….
La tangente en 2 a pour équation  , et la tangente en 0 a pour équation
, et la tangente en 0 a pour équation 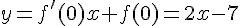 .
.
EXERCICE 52 :
Pour les fonctions simples :
– La fonction f est dérivable sur  , et sa fonction dérivée est f'(x) = 4x^3.
, et sa fonction dérivée est f'(x) = 4x^3.
– La fonction g est dérivable sur  , et sa fonction dérivée est g'(x) = 12x^11.
, et sa fonction dérivée est g'(x) = 12x^11.
– La fonction h est dérivable sur 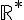 (l’ensemble des nombres réels non nuls), et sa fonction dérivée est
(l’ensemble des nombres réels non nuls), et sa fonction dérivée est 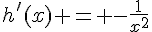 .
.
Pour les fonctions composées :
– Pour f, on peut identifier 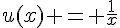 et
et 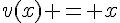 .
.
Les fonctions u et v sont toutes deux dérivables sur R*, et donc la fonction somme f est dérivable sur R*, et sa fonction dérivée est f'(x) = -1/x^2 + 1.
– Pour g, on peut identifier u(x) = -5 et  .
.
Les fonctions u et v sont toutes deux dérivables sur R* (avec une exception en x=0 pour v), et donc la fonction somme g est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est 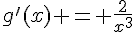 .
.
– Pour h, on peut identifier 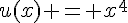 et
et 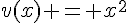 .
.
Les fonctions u et v sont dérivables sur R, et donc la fonction somme h est dérivable sur R, et sa fonction dérivée est 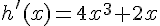 .
.
EXERCICE 53 :
Pour les fonctions composées :
– Pour f, on peut identifier 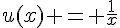 et
et 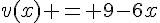 . La fonction u est dérivable sur R* (avec une exception en x=0), et la fonction v est dérivable sur R, donc la fonction produit f est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est
. La fonction u est dérivable sur R* (avec une exception en x=0), et la fonction v est dérivable sur R, donc la fonction produit f est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est 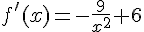 .
.
– Pour g, on peut identifier 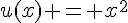 et
et 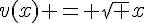 .
.
Les fonctions u et v sont dérivables sur 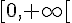 , donc la fonction produit g est dérivable sur
, donc la fonction produit g est dérivable sur 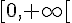 , et sa fonction dérivée est
, et sa fonction dérivée est 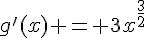 .
.
– Pour h, on peut identifier 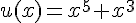 et
et 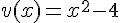 .
.
Les fonctions u et v sont dérivables sur R, donc la fonction produit h est dérivable sur R, et sa fonction dérivée est 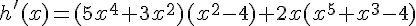 .
.
EXERCICE 54 :
1. On peut écrire 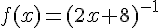 . On résout l’équation
. On résout l’équation 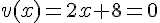 , ce qui donne
, ce qui donne 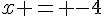 . Donc
. Donc 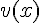 s’annule en
s’annule en 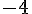 .
.
2. Le théorème de la dérivée de l’inverse d’une fonction affirme que si f est une fonction dérivable sur un intervalle I et à valeurs dans un intervalle J, alors si g est l’inverse de f, c’est-à-dire une fonction qui vérifie 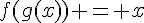 pour tout x de J, alors g est dérivable sur J et sa dérivée est donnée par la formule :
pour tout x de J, alors g est dérivable sur J et sa dérivée est donnée par la formule : 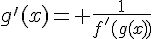 .
.
Ici, la fonction f est dérivable sur I et à valeurs dans ![]0,+\infty[](https://mathovore.fr/latex-images/2b03be02bbe34fd29b98639141bc65e6.png) , donc elle est bijective sur son ensemble de définition et admet une inverse.
, donc elle est bijective sur son ensemble de définition et admet une inverse.
On peut déterminer cette inverse en résolvant l’équation  en x :
en x :
on a 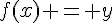 équivaut à
équivaut à 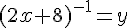 , soit
, soit 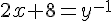 , soit
, soit 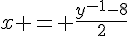 .
.
Donc l’inverse de f est la fonction 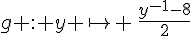 .
.
La dérivée de g en y est donnée par  , donc
, donc 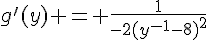 .
.
On peut donc exprimer 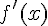 en fonction de x en utilisant la formule
en fonction de x en utilisant la formule 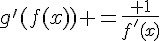 :
:
on a 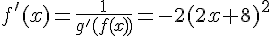 .
.
Donc f est dérivable sur I et sa dérivée est 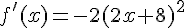 .
.
EXERCICE 55 :
1. On peut écrire 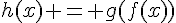 où
où  et
et 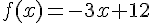 . Donc g est définie sur
. Donc g est définie sur 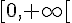 et f est dérivable sur I, donc h est définie et dérivable sur I.
et f est dérivable sur I, donc h est définie et dérivable sur I.
2. En utilisant la formule de la dérivée d’une fonction composée, on a 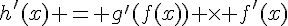 où
où 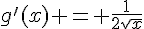 et
et 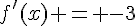 .
.
Donc 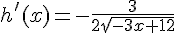 .
.
3. On a 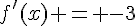 et
et 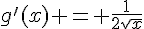 pour tout x strictement positif.
pour tout x strictement positif.
4. On a donc 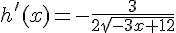 .
.
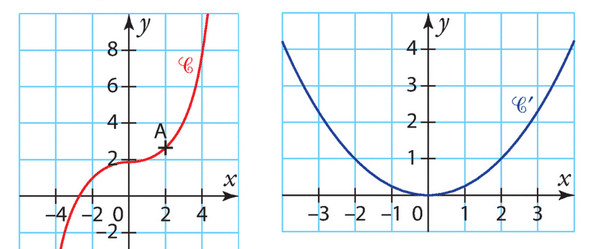
EXERCICE 56 :
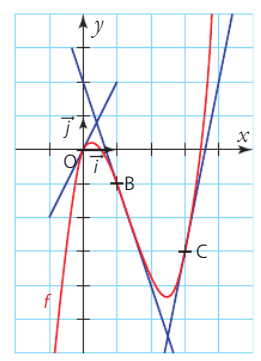
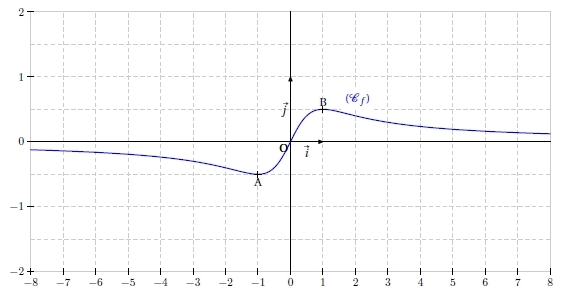
1. Graphiquement, on lit les pentes des tangentes en 0, 1 et 3 sur le graphe de f : la pente en 0 est nulle, la pente en 1 est négative et la pente en 3 est positive.
2. La tangente en C a pour coefficient directeur la dérivée en 3, soit f'(3) = 7. On utilise ensuite l’équation de la tangente en C : 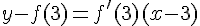 .
.
On a 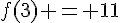 et donc l’équation réduite de la tangente en C est
et donc l’équation réduite de la tangente en C est 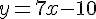 .
.
3. On calcule 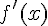 en dérivant
en dérivant 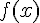 terme à terme :
terme à terme : 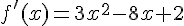 .
.
On trouve 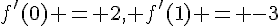 et
et 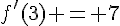 .
.
On peut vérifier que ces valeurs correspondent bien aux pentes des tangentes trouvées graphiquement. On peut également retrouver l’équation de la tangente en C en utilisant cette dérivée : 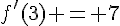 et
et 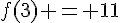 , donc l’équation réduite de la tangente en C est
, donc l’équation réduite de la tangente en C est  , soit
, soit 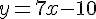 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «dérivée d’une fonction numérique : corrigé des exercices en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
Exercices de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.





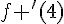 est négatif car la tangente en 4 est décroissante donc son coefficient directeur est négatif.
est négatif car la tangente en 4 est décroissante donc son coefficient directeur est négatif.