Calcul intégral : corrigé des exercices de maths en terminale en PDF.

Mis à jour le 19 septembre 2025

🔍Corrigés Détaillés

Terminale • Lycée

Calcul intégral

🔎 Analyse : 19 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en terminale sur le calcul d’une intégrale en utilisant une intégrale intermédiaire, ainsi que la propriété de linéarité (additivité).

Exercice 1 :

Calculer

$I= \int_{1}\;^{2}\frac{1+x^2}{1+x}dx$

en cherchant une intégrale intermédiaire de la forme

$J = \int_{1}\;^{2}\frac{f(x)}{g(x)}dx$ qui s’intégrera facilement.

On considère l’intégrale:

$J= \int_{1}\;^2 \frac{2x}{x+1}dx = [2ln(x+1)]_{1}^2 = 2ln\frac{3}{2}$

Calculons:

$I + J = \int_{1}\;^2 \frac{1+x^2}{1+x}dx\; + \int_{1}\;^2\frac{2x}{x+1} dx= \int_{1}\;^2 \frac{1+x^2+2x}{x+1} dx= \int_{1}\;^2\frac{(x+1)^2}{x+1}dx =\int_{1}\;^2 (x+1)dx = [\frac{x^2}{2} +x]_{1}^2 =\frac{5}{2}$

donc

$I = \frac{5}{2}-2ln(\frac{3}{2})$

Exercice 2 :

Calculer ces intégrales en intégrant par partiies:

A. $\int_{0}^{3}x\sqrt{3-x}dx$ .

Poson u=x u’=1

$v'=\sqrt{3-x}$ et $v=-\frac{2}{3}(3-x)^{\frac{^3}{2}}$

$A=[-\frac{2}{3}x(3-x)^{\frac{3}{2}}]+\int_{0}^{3} \frac{2}{3}(3-x)^{\frac{3}{2}}dx$

$A=0+ \frac{2}{3}\int_{0}^{3}(3-x)^{\frac{3}{2}}dx$

$A=\frac{2}{3}[-\frac{2}{5}(3-x)^{\frac{5}{2}}]$

$A=-\frac{2}{3}\times \frac{2}{5}[(3-x)^{\frac{5}{2}}]$

$A=-\frac{4}{15}\times ( -3^{\frac{5}{2}} )$

$A=\frac{4}{15}\times 3^{\frac{5}{2}}$

$A=\frac{4}{15}\times 3^2\times 3^{\frac{1}{2}}$

${\color{DarkRed} A=\frac{12}{5}\sqrt{3}}$

Exercice 3 :

Soit $f$ la fonction définie sur $\mathbb{R}^{+*}$ par $f(x)=\frac{1}{x}+\frac{lnx}{x}$ .

Quelle est la dérivée de $f$ sur $\mathbb{R}^{+*}$ ?

$f'(x)=-\frac{1}{x^2}+\frac{\frac{1}{x}\times x-lnx\times 1}{x^2}$

$f'(x)=-\frac{1}{x^2}+\frac{1-lnx}{x^2}$

$f'(x)=\frac{-1+1-lnx}{x^2}$

$f'(x)=-\frac{lnx}{x^2}$

Exercice 4 :

1. a. On a $f(x) = \sqrt{x^2-x}+x$ .

En utilisant le développement asymptotique de $\sqrt{1-x}$ en $x=0$ , on a $\sqrt{x^2-x} = x\sqrt{1-\frac{1}{x}} \sim x(1-\frac{1}{2x}) = x-\frac{1}{2}$ quand $x$ tend vers l’infini. Ainsi, $f(x) \sim x$ quand $x$ tend vers l’infini.

Donc la limite de $f$ en l’infini est $+\infty$ .

b. On peut remarquer que $f(-x) = \sqrt{x^2+x}-x$ .

En utilisant le développement asymptotique de $\sqrt{1+x}$ en $x=0$ , on a $\sqrt{x^2+x} = x\sqrt{1+\frac{1}{x}} \sim x(1+\frac{1}{2x}) = x+\frac{1}{2}$ quand $x$ tend vers l’infini. Ainsi, $f(-x) \sim -\frac{1}{2}$ quand $x$ tend vers l’infini. Donc la limite de $f$ en $-\infty$ est $-\frac{1}{2}$ .

La fonction $f$ n’est pas définie en $x=0$ , donc il n’y a pas de limite de $f$ en $0$ , et f admet une discontinuité en $x=0$ .

La fonction $f$ est définie et continue sur $[1,+\infty[$ , donc sa limite en l’infini par la gauche est égale à $f(1)=\sqrt{1}+1=2$ .

2. La fonction $f$ n’est pas dérivable en $0$ , car elle n’est pas définie en $0$ . En revanche, pour $x>0$ , on a
$f'(x) = \frac{x-x^2^{-1/2}}{2\sqrt{x-x^2}},$
donc $f'(0)$ n’existe pas.

La fonction $f(x)$ est discontinue en $x=0$ et n’est pas dérivable en $x=0$ , car la fonction $\sqrt{x^2-x}$ n’est pas dérivable en $x=0$ .

De même, $f(x)$ est discontinue et non dérivable en $x=1$ , car la fonction $\sqrt{x^2-x}$ n’est pas dérivable en $x=1$ .

3. a. On a
$\lim_{x\to \infty} \frac{f(x)}{x} = \lim_{x\to \infty} \frac{\sqrt{x^2-x}+x}{x} = \lim_{x\to \infty} (\sqrt{1-\frac{1}{x}} + 1) = 2.$

b. On a
$f(x)-2x = (\sqrt{x^2-x}-x) + x.$

En utilisant le développement asymptotique de $\sqrt{1-x}$ en $x=0$ , on a

$\sqrt{x^2-x} = x\sqrt{1-\frac{1}{x}} \sim x(1-\frac{1}{2x}) = x-\frac{1}{2}$ , donc
$f(x)-2x \sim (x - \frac12) + x = 2x - \frac{1}{2}.$

Ainsi, la limite de $f(x)-2x$ en l’infini est $+\infty$ . On en déduit que la courbe de $f$ admet une asymptote oblique d’équation $y=2x-\frac{1}{2}$ en l’infini.

Exercice 5 :

1.a. On a
$f(x) = \frac{-2x^2+3x+7}{x-3} = \frac{-(2x+1)(x-7)}{x-3}.$

Ainsi, quand $x$ tend vers l’infini, le terme $(2x+1)$ l’emporte sur l’autre terme, donc $f(x)$ tend vers $-2$ . De même, quand $x$ tend vers moins l’infini, le terme $-(x-7)$ l’emporte sur l’autre terme, donc $f(x)$ tend vers $2$ .

b. On peut écrire
$f(x) = \frac{-(2x+1)(x-7)}{x-3} = -2x - \frac{13}{x-3}.$
Ainsi, quand $x$ tend vers $3$ par la gauche, le deuxième terme tend vers moins l’infini, donc $f(x)$ tend vers $+\infty$ . Quand $x$ tend vers $3$ par la droite, le deuxième terme tend vers plus l’infini, donc $f(x)$ tend vers $-\infty$ . On peut interpréter ces résultats graphiquement en remarquant que la courbe de $f$ possède une asymptote verticale en $x=3$ , c’est-à-dire que la fonction n’est pas continue en $x=3$ .

2.a. La dérivée de $f$ est donnée par
$f'(x) = \frac{-2(x-3)(2x+1) - (-2x^2+3x+7)}{(x-3)^2} = \frac{-4x-5}{(x-3)^2}.$
Cette fonction est définie pour tout $x\neq 3$ . Elle est positive pour $x<-\frac{5}{4}$ et négative pour $x>-\frac{5}{4}$ , donc $f$ est décroissante sur $]-\infty, -\frac{5}{4}]$ et croissante sur $[-\frac{5}{4}, 3[$ et $]3,+\infty[$ .

Le tableau de variation complet de $f$ est le suivant :

$\begin{array}{|c|ccc|c|}\,\hline\,x\,-\infty\,\,-\frac{5}{4}\,\,3\,+\infty\\\,\hline\,f'(x)\,++--\\\,\hline\,f(x)\,\searrow\,\,\text{discontinuite}\,\,\nearrow\\\,\hline\,\end{array}$

3.a. La droite (D) d’équation $y=-2x-3$ est une asymptote oblique de $f$ en l’infini si et seulement si
$\lim_{x\to\infty} [f(x) - (-2x-3)] = 0.$
On a
$f(x) - (-2x-3) = \frac{-2x^2+3x+7}{x-3} + 2x+3 = \frac{13x+22}{x-3}.$
Ainsi, on a
$\lim_{x\to\infty} [f(x) - (-2x-3)] = \lim_{x\to\infty} \frac{13x+22}{x-3} = 13.$

Donc la droite (D) est une asymptote oblique de $f$ en l’infini.

b. La fonction $f(x)-(-2x-3) = \frac{13x+22}{x-3}$ est positive pour $x>3$ , ce qui signifie que la courbe de $f$ est située en dessous de la droite (D) pour $x$ assez grand (dans les valeurs de $x$ où $f$ est définie).

Ainsi, la droite (D) est une asymptote oblique à la courbe de $f$ en l’infini, et la courbe de $f$ est en dessous de la droite pour $x$ assez grand.

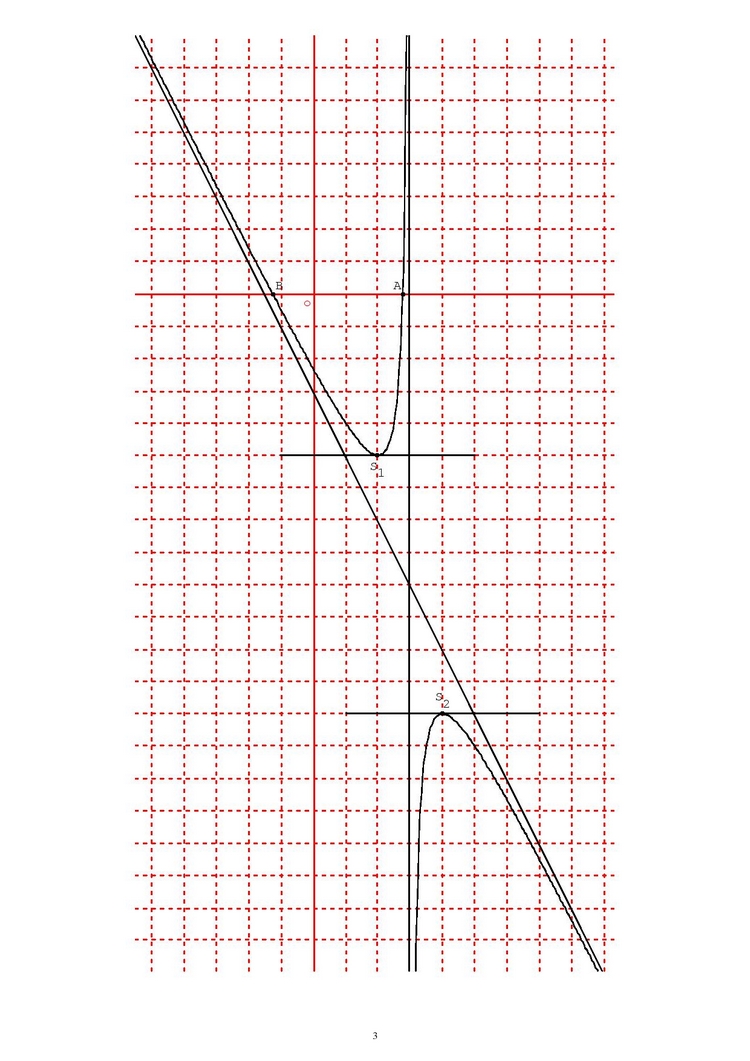
4. Le point $S(3;-9)$ est sur la droite verticale $x=3$ , qui est une asymptote verticale de la courbe de $f$ .

La courbe de $f$ est symétrique par rapport à la droite $x=3$ , car si on remplace $x$ par $3+\epsilon$ avec $\epsilon \neq 0$ , alors $f(x)$ est remplacé par $f(6-\epsilon)$ , qui est égal à $f(3-\epsilon)$ car les deux termes $-(2x+1)$ et $(x-7)$ sont symétriques par rapport à $x=3$ .

Ainsi, on peut en déduire que le point $S$ est le centre de symétrie de la courbe de $f$ .

Les points d’intersection de la courbe de $f$ avec l’axe des abscisses sont les solutions de l’équation $f(x)=0$ , c’est-à-dire
$-2x^2+3x+7 = 0 \quad \Leftrightarrow \quad x = \frac{3\pm\sqrt{29}}{4}.$

5. Voici la courbe de $f$ avec ses éléments remarquables :

Exercice 6 :

On considère la suite $( U_n)$ définie, pour tout entier naturel n , par :

$U_n=\int_{0}^{1}\frac{e^{-nx}}{1+e^{-x}}dx$

a. Montrer que $U_0+U_1=1$ .

b. Calculer $U_1$ , en déduire $U_0$ .

2. Montrer que, pour tout entier naturel n, $U_n\geq\, 0$ .

a. Montrer que, pour tout entier naturel n non nul,

$U_{n+1}+U_n=\frac{1-e^{-n}}{n}$

b. En déduire que, pour tout entier naturel n non nul,

$U_n\leq\, \frac{1-e^{-n}}{n}$

4. Déterminer la limite de la suite $( U_n)$ .

Exercice 7 :

1. a. On a $f(x) = (1+x)e^{-x}$ . Le facteur $(1+x)$ est toujours positif, et le facteur $e^{-x}$ est positif pour tout $x$ . Ainsi, $f(x)$ est toujours positif sur $\mathbb{R}$ .

b. La limite de $f(x)$ en $-\infty$ est $0$ , car $e^{-x}$ tend vers l’infini quand $x$ tend vers $-\infty$ plus vite que $(1+x)$ ne tend vers l’infini.

La limite de $f(x)$ en $+\infty$ est aussi $0$ , car le facteur $(1+x)$ est négligeable devant $e^{-x}$ quand $x$ tend vers l’infini.

c. On a $f'(x) = -xe^{-x}$ , donc $f'(x)$ est négative pour $x>0$ et positive pour $x<0$ .

Ainsi, $f$ est décroissante sur $]-\infty, 0]$ et croissante sur $[0, +\infty[$ .

d. Voici la courbe de la fonction $f$ :
![Graph of f(x)](https://i.imgur.com/pJWUwK3.png)

2. a. Pour tout $n\in\mathbb{N}$ , on a $I_n = \int_{-1}^{n} f(x) dx > 0$ car $f(x)$ est toujours positif sur $\mathbb{R}$ .

b. Pour $n\geq\, 0$ , on a
$I_{n+1} - I_n = \int_{n}^{n+1} f(x) dx \geq\, 0$
car $f(x)$ est positive sur tout $\mathbb{R}$ . Pour $n<0$ , on a
$I_{n+1} - I_n = \int_{n}^{n+1} f(x) dx \geq\, \int_{-1}^{0} f(x) dx > 0$
car $f(x)$ est croissante sur $[-1,0]$ . Ainsi, par récurrence, on en déduit que $(I_n)$ est une suite croissante.

3. a. On utilise une intégration par parties avec $u = (1+x)$ (donc $du = dx$ ) et $dv = e^{-x} dx$ (donc $v = -e^{-x}$ ) :
$\begin{align*}\,\int_{a}^{b}\,f(x)\,dx\,=\,[(1+x)(-e^{-x})]_a^b\,-\,\int_a^b\,(-e^{-x})\,dx\,\\\,=\,-(1+b)e^{-b}\,+\,(1+a)e^{-a}\,-\,[e^{-x}]_a^b\,\\\,=\,-(1+b)e^{-b}\,+\,(1+a)e^{-a}\,+\,e^{-a}\,-\,e^{-b}\,\\\,=\,(2+a)e^{-a}\,-\,(2+b)e^{-b}.\,\end{align*}$

b. On a
$\begin{align*}\,I_n\,=\,\int_{-1}^n\,f(x)\,dx\,=\,\int_{-1}^0\,f(x)dx\,+\,\int_{0}^1\,f(x)dx\,+\,\cdots\,+\,\int_{n-1}^n\,f(x)dx\,\\\,=\,\sum_{k=0}^{n-1}\,\int_k^{k+1}\,f(x)dx\,\\\,=\,\sum_{k=0}^{n-1}\,[(2+k)e^{-k}\,-\,(3+k)e^{-(k+1)}]\,\\\,=\,2e^{-0}\,-\,(3\,+\,1)e^{-1}\,+\,3e^{-1}\,-\,(4\,+\,1)e^{-2}\,+\,\cdots\,-\,(n+1)\,e^{-(n-1)}\,+\,ne^{-n}\,\\\,=\,(2\,-\,4e^{-1}\,-\,(n+1)e^{-(n-1)})\,+\,\sum_{k=2}^{n}\,[(2+k)e^{-k}-(3+k)e^{-(k+1)}].\,\end{align*}$

c. On a
$\lim_{n\to\infty} I_n = \lim_{n\to\infty} \sum_{k=0}^{n-1} [(2+k)e^{-k} - (3+k)e^{-(k+1)}] = \sum_{k=0}^{\infty} [(2+k)e^{-k} - (3+k)e^{-(k+1)}].$
Or, on a
$(2+k)e^{-k} - (3+k)e^{-(k+1)} = \frac{k+1}{e^{k+1}} - \frac{1}{e^k},$
et la série de terme général $\frac{k+1}{e^{k+1}}$ converge, donc la série ci-dessus converge absolument.

Ainsi, on peut permuter les termes de la somme, ce qui donne
$\lim_{n\to\infty} I_n = [\frac{1}{e^x}]_{x=0}^{\infty} = 0 - \frac{1}{e^0} = -1.$

d. La limite de $I_n$ en l’infini est $-1$ .

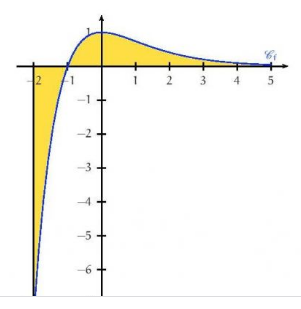
Graphiquement, cela signifie que la zone délimitée par la courbe de $f$ et les droites d’équation $x=-1$ et $x=n$ a une aire qui tend vers $-1$ quand $n$ tend vers l’infini.

4. On cherche $\alpha$ tel que $\int_{-1}^{\alpha} f(x) dx = e$ .

On résout l’équation obtenue en utilisant l’intégration par parties de la question 3.a :
$(2+\alpha)e^{-\alpha} - (2+(-1))e^{-(-1)} = e.$

On peut récrire cette équation sous la forme
$2e^{-\alpha} +(\alpha-1)e^{-\alpha} = e^{-1} + 1,$
ou encore
$(\alpha-1)e^{-\alpha} = e^{-1} + 1 - 2e^{-\alpha}.$

On remarque que la fonction $x\mapsto e^{-x}$ est décroissante et positive pour tout $x$ , donc l’équation ci-dessus admet une unique solution $\alpha$ sur $\mathbb{R}$ .

On peut donc la résoudre numériquement pour obtenir
$\alpha \approx 0.368.$
Ce calcul intégral correspond à un calcul d’aire, car $\int_{-1}^{\alpha} f(x) dx$ représente l’aire de la partie du plan comprise entre l’axe des abscisses, la courbe de $f$ et les droites d’équations $x=-1$ et $x=\alpha$ .

Exercice 8 :

1. On utilise la formule $(\cos^2 x)' = -2\sin x \cos x$ pour calculer $f'(x)$ :
$\begin{align*}\,f'(x)\,=\,4\cos^3\,x\,(-\sin\,x)\,-\,2\cos^3\,x\,\sin\,x\,\\\,=\,-2\cos^3\,x\,\sin\,x\,(1\,-\,2\cos^2\,x)\,\\\,=\,-2\cos^3\,x\,\sin\,x\,\sin^2\,x\,\\\,=\,-2\cos^3\,x\,(1-\cos^2\,x)\,\sin\,x\,\\\,=\,-2\cos^3\,x\,\sin\,x\,+\,2\cos^5\,x\,\sin\,x.\,\end{align*}$

Ensuite, on utilise la formule $(\cos^2 x)'' = -2\cos x \sin x (\cos^2 x + \sin^2 x) = -2\cos x \sin x$ pour calculer $f''(x)$ :
$\begin{align*}\,f''(x)\,=\,-2\cos^2\,x\,\sin^2\,x\,-\,2\cos^3\,x\,\cos\,x\,+\,10\cos^4\,x\,\sin^2\,x\,\\\,=\,-2\cos\,x\,\sin\,x\,(\cos\,x\,\sin\,x\,+\,4\cos^2\,x\,-\,5\cos^2\,x\,\sin^2\,x).\,\end{align*}$

On peut vérifier que $f''(x) + 16f(x) = -32\cos^5 x \sin x + 16\cos^4 x \sin x + 16\cos^6 x - 16\cos^5 x = 16\cos^4 x (\cos x-1)^2$ , qui est bien une constante.

2. On utilise la formule de changement de variables $t=\cos^2 x$ pour calculer l’intégrale $I$ :
$\begin{align*}\,I\,=\,\int_0^{\frac{\pi}{2}}\,f(x)\,dx\,=\,\int_0^{\frac{\pi}{2}}\,\cos^4\,x\,-\,\cos^2\,x\,dx\\\,=\,\int_0^1\,t^2\,-\,t\,dt\,=\,[\frac{1}{3}\,t^3\,-\,\frac{1}{2}\,t^2]_0^1\,\\\,=\,\frac{1}{6}.\,\end{align*}$

Exercice 9 :

Calculer :

$I=\int_{1}^{x}(t^2-t)ln\,t\,dt$

Posons :

$u=lnt\,\,u'=\frac{1}{t}$ et $v'=t^2-t\,\,\,\,v=\frac{t^3}{3}-\frac{t^2}{2}$

$I=,[,(\frac{t^3}{3}-\frac{t^2}{2})lnt,,]-\int_{1}^{x}\frac{1}{t}\times ,(\frac{t^3}{3}-\frac{t^2}{2})$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-\int_{1}^{x}\frac{1}{t}\times ,(\frac{t^3}{3}-\frac{t^2}{2})$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-\int_{1}^{x},\frac{t^2}{3}-\frac{t}{2}$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-,[,\frac{t^3}{9}-\frac{t^2}{4},]$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-(,\frac{x^3}{9}-\frac{x^2}{4}-\frac{1}{9}+\frac{1}{4})$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-\frac{x^3}{9}+\frac{x^2}{4}+\frac{1}{9}-\frac{1}{4}$

$I=(\frac{x^3}{3}-\frac{x^2}{2})lnx\,,-\frac{x^3}{9}+\frac{x^2}{4}-\frac{5}{36}$

Exercice 10 :

$f(x)=-1+x+\frac{x^3}{2}+x^5 \\ F(x)=-x+\frac{x^2}{2}+\frac{x^4}{8}+\frac{x^6}{6}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=(x-1)^2(x+1)=(x-1)(x^2-1)=x^3-x^2-x+1 \\ F(x)=\frac{x^4}{4}-\frac{x^3}{3}-\frac{x^2}{2}+x+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{5}{4}x+\frac{7}{3}x^2+{1}{2}x^4 \\ F(x)=\frac{5}{8}x^2+\frac{7}{9}x^3+\frac{12}{5}x^5+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=x+\frac{1}{\sqrt{x}} \\ F(x)=\frac{x^2}{2}+2\sqrt{x}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=-\frac{1}{x^2}+\frac{1}{x^3} \\ F(x)=\frac{1}{x}+\frac{-1}{2x^2}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{-3}{(3x-1)^2}\,.$

$F(x)=-\frac{1}{(3x-1)}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=cos(x)+sin(x)\,.$

$F(x)=sin(x)-sin(x)+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{-3}{\sqrt{6x+7}}\,.$

$F(x)=\frac{-\sqrt{6x+7}}{2}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{1}{cos^2(x)}+cos x\,.$

$F(x)=tan x + sinx+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=ln(x)\,.$

$F(x)=xln(x)-x+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=sinx\times cos^2 x\,.$

$F(x)=-\frac{ cos^3 x}{3}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=sin(-3x+1)\,.$

$F(x)=\frac{cos(-3x+1)}{3}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{3x}{(x^2+1)^2}\,.$

$F(x)=-\frac{3}{2(x^2+1)}+k\,\,(k\,\in\,\mathbb{R}\,).$

$f(x)=\frac{-1}{sin^2 x}=\frac{-cos^2 x-sin^2 x}{sin^2 x}\,.$

$F(x)=\frac{cos x}{sin x}+k=\frac{1}{tanx}+k=cotan x+k\,\,(k\,\in\,\mathbb{R}\,).$

Exercice 11 :

1. On utilise la formule $(\cos^2 x)' = -2\sin x \cos x$ pour calculer $f'(x)$ :

$\begin{align*}\,f'(x)\,=\,4\cos^3\,x\,(-\sin\,x)\,-\,2\cos^3\,x\,\sin\,x\,\\\,=\,-2\cos^3\,x\,\sin\,x\,(1\,-\,2\cos^2\,x)\,\\\,=\,-2\cos^3\,x\,\sin\,x\,\sin^2\,x\,\\\,=\,-2\cos^3\,x\,(1-\cos^2\,x)\,\sin\,x\,\\\,=\,-2\cos^3\,x\,\sin\,x\,+\,2\cos^5\,x\,\sin\,x.\,\end{align*}$

Ensuite, on utilise la formule $(\cos^2 x)'' = -2\cos x \sin x (\cos^2 x + \sin^2 x) = -2\cos x \sin x$ pour calculer $f''(x)$ :

$\begin{align*}\,f''(x)\,=\,-2\cos^2\,x\,\sin^2\,x\,-\,2\cos^3\,x\,\cos\,x\,+\,10\cos^4\,x\,\sin^2\,x\,\\\,=\,-2\cos\,x\,\sin\,x\,(\cos\,x\,\sin\,x\,+\,4\cos^2\,x\,-\,5\cos^2\,x\,\sin^2\,x).\,\end{align*}$

On peut vérifier que $f''(x) + 16f(x) = -32\cos^5 x \sin x + 16\cos^4 x \sin x + 16\cos^6 x - 16\cos^5 x = 16\cos^4 x (\cos x-1)^2$ , qui est bien une constante.

Exercice 12 :
On considère trois réels a, b, c tels que , pour tout $x\in ]0;+\infty[$ :

$\frac{1}{x(1+x)^2}=\frac{a}{x}+\frac{b}{1+x}+\frac{c}{(1+x)^2}$ .

$\frac{1}{x(1+x)^2}=\frac{a(1+x)^2}{x(1+x)^2}+\frac{bx(1+x)}{x(1+x)^2}+\frac{cx}{x(1+x)^2}$ .

$\frac{1}{x(1+x)^2}=\frac{(a+b)x^2+(2a+b+c)x+a}{x(1+x)^2}$ .

Par identification, nous obtenons le système :

${a+b = 0 \\ 2a+b+c = 0 \\ a = 1$

${b = -1 \\ c = -1 \\ a = 1$

donc

$\frac{1}{x(1+x)^2}=\frac{1}{x}-\frac{1}{1+x}-\frac{1}{(1+x)^2}$

2. Soit $X\ge 1$ .

a. Calculer

$\int_{1}^{X} \frac{dx}{x(1+x)^2}=\int_{1}^{X} \frac{1}{x}-\frac{1}{1+x}-\frac{1}{(1+x)^2}dx$ .

$=[ln(x)-ln(1+x)+\frac{1}{1+x}]$

$=ln(X)-ln(1+X)+\frac{1}{1+X}+ln 2 -\frac{1}{2}$

$=ln(\frac{X}{1+X})+\frac{1}{1+X}+ln 2 -\frac{1}{2}$

b. Soit f la fonction définie sur $x\in [1;+\infty[$ par

$f(X)=\int_{1}^{X} \frac{ln x}{(1+x)^3}dx$

En intégrant par parties, calculer f(X) en fonction de X .

Posons :

u(x)= lnx alors $u'(x)=\frac{1}{x}$

$v'(x)=\frac{1}{(1+x)^3$ alors $v(x)= \frac{-1}{2(1+x)^2}$

Donc :

$f(X)=\int_{1}^{X} \frac{ln x}{(1+x)^3}dx=[\frac{-lnx}{2(1+x)^2}]+\int_{1}^{X} \frac{1}{2x(1+x)^2}dx$

$f(X)=\int_{1}^{X} \frac{ln x}{(1+x)^3}dx=\frac{-lnX}{2(1+X)^2}+\frac{1}{2}\int_{1}^{X} \frac{1}{x(1+x)^2}dx$

$f(X)=\int_{1}^{X} \frac{ln x}{(1+x)^3}dx=\frac{-lnX}{2(1+X)^2}+\frac{1}{2}(ln(\frac{X}{1+X})+\frac{1}{1+X}+ln 2 -\frac{1}{2})$

$f(X)=\int_{1}^{X} \frac{ln x}{(1+x)^3}dx=\frac{-lnX}{2(1+X)^2}+\frac{1}{2}(ln(\frac{X}{1+X})+\frac{1}{1+X})+\frac{1}{2}(ln 2 -\frac{1}{2})$

c. or :

$\lim_{X \to +\infty} \frac{-lnX}{2(1+X)^2}+\frac{1}{2}(ln(\frac{X}{1+X})+\frac{1}{1+X})=0$

donc:

$\lim_{X \to +\infty} f(X)=\frac{1}{2}(ln2-\frac{1}{2})$

Exercice 13 :

1. On peut écrire :
$\frac{1}{x(1+x)^2} = \frac{a}{x} + \frac{b}{1 + x} + \frac{c}{(1+x)^2} = \frac{a(1 + x)^2c + bx + cx^2}{x(1 + x)^2}.$

En identifiant les coefficients des polynômes, on trouve :
$a + b = 0 \quad \text{et} \quad ac = \frac{1}{4} \quad \text{et} \quad bc + c = -\frac{1}{4}.$

On peut prendre par exemple $b = -a$ pour que la première équation soit vérifiée, alors la troisième donne $-a^2 c - c = -\frac{1}{4}$ , soit $c(1 + a^2) = \frac{1}{4}$ , d’où $c = \frac{1}{4(1+a^2)}$ et $a^2 c + c = -\frac{1}{4}$ implique $a = -\frac{1}{2}$ , donc $b = \frac{1}{2}$ et $c = \frac{1}{8}$ .

2. a. On utilise la décomposition trouvée précédemment :
$\frac{1}{x(1+x)^2} = -\frac{1}{2x} + \frac{1}{1+x} + \frac{1}{8}(\frac{1}{1+x} - \frac{1}{(1+x)^2}).$

En intégrant :
$\begin{align*}\,\int_1^X\,\frac{1}{x(1+x)^2}\,dx\,=\,-\frac{1}{2}\,\ln\,x\,\Bigg|_1^X\,+\,\ln(1\,+\,x)\,\Bigg|_1^X\,+\,\frac{1}{8}\,\int_1^X\,(\frac{1}{1+x}\,-\,\frac{1}{(1+x)^2})\,dx\,\\\,=\,\frac{1}{2}\,\ln\,\frac{X}{1}\,+\,\ln(1\,+\,X)\,-\,\ln\,2\,+\,\frac{1}{8}\,[\ln(1\,+\,x)\,+\,\frac{1}{1+x}]_1^X\,\\\,=\,\frac{1}{2}\,\ln\,X\,-\,\frac{1}{2}\,\ln\,2\,+\,\ln(1\,+\,X)\,-\,\frac{1}{8}\,\ln(\frac{X+1}{2X}).\,\end{align*}$

b. On utilise l’intégration par parties avec $u = \ln x$ et $dv = \frac{1}{(1+x)^3} dx$ :
$\begin{align*}\,f(X)\,=\,\int_1^X\,\frac{\ln\,x}{(1+x)^3}\,dx\,=\,-\frac{\ln\,x}{2(1+x)^2}\,\Bigg|_1^X\,+\,\frac{1}{2}\,\int_1^X\,\frac{dx}{x(1+x)^2}\,\\\,=\,-\frac{\ln\,X\,-\,\ln\,1}{2(1+X)^2}\,+\,\frac{1}{2}\,\int_1^X\,\frac{dx}{x(1+x)^2}\,\\\,=\,-\frac{\ln\,X}{2(1+X)^2}\,+\,\frac{1}{4(1+X)}\,+\,\frac{1}{8}(\frac{1}{1+X}\,-\,\frac{1}{(1+X)^2})\,-\,\frac{1}{8}.\,\end{align*}$

Ainsi, on trouve
$\begin{align*}\,\lim_{X\,\to\,+\infty}\,f(X)\,=\,\lim_{X\,\to\,+\infty}\,(-\frac{\ln\,X}{2(1+X)^2}\,+\,\frac{1}{4(1+X)}\,+\,\frac{1}{8}(\frac{1}{1+X}\,-\,\frac{1}{(1+X)^2})\,-\,\frac{1}{8})\,\\\,=\,-\frac{1}{8}.\,\end{align*}$

c. On a
$\begin{align*}\,\frac{1}{2}(\ln\,2\,-\,\frac{1}{2})\,-\,f(X)\,=\,\frac{1}{2}\,\ln(\frac{2}{X})\,-\,\frac{1}{2(1+X)^2}\,-\,\frac{1}{8}(\frac{X}{1+X}\,-\,\frac{1}{1+X}\,+\,\frac{1}{(1+X)^2})\,\\\,=\,\frac{1}{2}\,\ln(\frac{2}{X})\,-\,\frac{1}{2(1+X)^2}\,-\,\frac{1}{8}\,+\,\frac{9}{8(1+X)}\,-\,\frac{1}{8(1+X)^2}.\,\end{align*}$

Les termes en $-\frac{1}{2(1+X)^2}$ et $-\frac{1}{8}$ tendent vers $0$ quand $X \to +\infty$ , et on a
$\lim_{X \to +\infty} \frac{1}{2} \ln(\frac{2}{X}) = 0 \quad \text{et} \quad \lim_{X \to +\infty} \frac{9}{8(1+X)} = \lim_{X \to +\infty} \frac{1}{8(1+X)^2} = 0.$

Ainsi,
$\lim_{X \to +\infty} (\frac{1}{2}(\ln 2 - \frac{1}{2}) - f(X)) = 0,$
ce qui montre que $\lim_{X \to +\infty} f(X) = \frac{1}{2}(\ln 2 - \frac{1}{2})$ .

Exercice 14 :
Calculer l’intégrale proposée :

b. $\int_{-1}^{2}-x+6dx=[-\frac{x^2}{2}+6x]=-\frac{2^2}{2}+12+\frac{1}{2}+6=16,5$

c. $\int_0^{4} (2x^2+8x-1) dx=[2\frac{x^3}{3}+4x^2-x]\\=2\times \frac{4^3}{3}+4\times 4^2-4 -2\times \frac{0^3}{3}-4\times 0^2+0\\=\frac{128}{3}+64-4=\frac{308}{3}.$

d. $\int_0^{\frac{2\pi}{3}} (cosx) dx=[sin x]\\=\sin{ \frac{2\pi}{3}} -sin 0 =-\frac{\sqrt{3}}{2}.$

e. $\int_{-2}^{0} (x^5+4x^3+x^2-x) dx =[\frac{x^6}{6}+x^4+\frac{x^3}{3}-\frac{x^2}{2}]\\=\frac{0^6}{6}+0^4+\frac{0^3}{3}-\frac{0^2}{2} -\frac{(-2)^6}{6}-(-2)^4-\frac{(-2)^3}{3}+\frac{(-2)^2}{2} \\=-\frac{64}{6}-16-\frac{8}{3}+2=-\frac{66}{3}.$

f. $\int_1^{3} (\frac{1}{x^2}) dx \\= [-\frac{1}{x}]=-\frac{1}{3}+\frac{1}{1}=\frac{2}{3}.$

g. $\int_{\frac{-\pi}{4}}^{\frac{\pi}{4}}(\frac{1}{cos^2 x}) dx\\=2\times \int_{0}^{\frac{\pi}{4}}(\frac{1}{cos^2 x}) dx=2\times [ln(cos x)]=2ln(\frac{\sqrt{2}}{2}).$

h. $\int_{3}^{4}(\frac{1}{\sqrt{2x+5}}) dx=[\sqrt{2x+5}]\\=\sqrt{2\times 4+5}-\sqrt{2\times 3+5}\\=\sqrt{13}-\sqrt{11}.$

Exercice 15 :

Soit $f(x)=x^2+1 \,.$

$\int_{-1}^{0}(x^2+1) dx=[\frac{x^3}{3}+x]=\frac{0^3}{3}+0-\frac{(-1)^3}{3}+1=\frac{2}{3}.$

Exercice 16 :

On considère

$\int_a^{b} f(x) dx=5 \,.$ et $\int_a^{b} g(x) dx=3 \,.$

a. $\int_a^{b} (2f(x)-4g(x)) dx=-2 \,.$

b. $\beta =6.$

Exercice 17 :

$\int_{-5}^{5} (x^3-tan x) dx=0 \,.$

car la fonction est impaire sur l’intervalle [-5;5] centré en 0.

Exercice 18 :

a. On peut linéariser $\sin^2 x$ en utilisant l’identité trigonométrique $\sin^2 x = \frac{1-\cos(2x)}{2}$ :
$\int_0^{\frac{\pi}{2}} \sin^2 x dx= \frac{1}{2}\int_0^{\frac{\pi}{2}} dx - \frac{1}{2}\int_0^{\frac{\pi}{2}} \cos(2x) dx = \frac{\pi}{4}.$
b. On utilise la formule $\sin(2x) = 2\sin x \cos x$ :
$\int_0^{\frac{\pi}{4}} \sin x \cos x dx = \frac{1}{2}\int_0^{\frac{\pi}{4}} \sin(2x) dx = \frac{1}{4}[-\cos(2x)]_0^{\frac{\pi}{4}} = \frac{1}{4}(1-\sqrt{2}/2).$

Exercice 19 :

a. On peut écrire :
$\frac{-6t-3}{(t+2)^2(t-1)^2} = \frac{a}{(t+2)^2}+\frac{b}{(t-1)^2} = \frac{a}{t+2} - \frac{2a}{(t+2)^2} + \frac{b}{t-1} - \frac{2b}{(t-1)^2}.$

En multipliant par $(t+2)^2(t-1)^2$ , on obtient :
$-6t-3 = a(t-1)^2 + b(t+2)^2.$

Pour $t = -1$ , cela donne $-6a = 3$ , donc $a = -\frac{1}{2}$ . Pour $t = -2$ , on a $4b = 9$ , donc $b = \frac{9}{4}$ .

Finalement :
$\frac{-6t-3}{(t+2)^2(t-1)^2} = \frac{-1/2}{t+2}+\frac{9/4}{(t-1)^2}.$

b. On peut intégrer la première fraction en utilisant une substitution $u = t+2$ , $du = dt$ :
$\int \frac{-1/2}{t+2} dt = \int \frac{-1/2}{u} du = -\frac{1}{2}\ln|u| + C = -\frac{1}{2} \ln|t+2| + C.$

Pour la deuxième fraction, on peut utiliser une substitution $v = t - 1$ , $dv = dt$ :
$\begin{align*}\,\int\,\frac{9/4}{(t-1)^2}\,dt\,=\,\int\,\frac{9/4}{v^2}\,dv\,=\,\frac{9}{4}\,\int\,v^{-2}\,dv\,\\\,=\,-\frac{9}{4v}\,+\,C\,=\,-\frac{9}{4(t-1)}\,+\,C.\,\end{align*}$

Exercice 20 :

a) L’intégrale de $3dx$ entre 0 et 4 vaut :

$\int_{0}^{4}3dx=3\times (4-0)=12$

b) L’intégrale de $(\frac{1}{2}t+2)dt$ entre 3 et 7 vaut :

$\int_{3}^{7}(\frac{1}{2}t+2)dt=[\frac{1}{4}t^2+2t]_{3}^{7}=(\frac{1}{4}(7)^2+2(7))-(\frac{1}{4}(3)^2+2(3))=15$

Exercice 21 :

Pour déterminer si les fonctions proposées sont des primitives de f, il suffit de dériver chaque fonction et de voir si on obtient f.

a) On a : $F'_1(x)=\frac{e^x}{\,(e^x+1\,\,)^2}\times \frac{-1}{e^x+1}=-\frac{e^x}{\,(e^x+1\,\,)^3}$

$F'_1(x)$ est différente de f(x), donc $F_1(x)$ n’est pas une primitive de f(x).

b) On a : $F'_2(x)=\frac{e^x}{\,(e^x+1\,\,)^2}\times \frac{2e^x+1}{e^x+1}-\frac{e^x}{\,(e^x+1\,\,)^2}\times \frac{(2e^x+1)^2}{\,(e^x+1\,\,)^2}=\frac{e^x}{\,(e^x+1\,\,)^3}(e^x-1)$

$F'_2(x)$ est égale à f(x), donc $F_2(x)$ est une primitive de f(x).

c) On a : $F'_3(x)=\frac{-2e^{-2x}}{\,(e^{-x}+1\,\,)^2}-\frac{(2e^{-x}+1)(-e^{-x})}{\,(e^{-x}+1\,\,)^2}=-\frac{e^{-x}}{\,(e^{-x}+1\,\,)^2}$

$F'_3(x)$ est différente de f(x), donc $F_3(x)$ n’est pas une primitive de f(x).

d) On a : $F'_4(x)=\frac{-e^{-x}(e^{-x}+2)}{\,(e^{-x}+1\,\,)^2}+\frac{(e^{-x}+2)(-e^{-x})}{\,(e^{-x}+1\,\,)^2}=-\frac{e^{-x}}{\,(e^{-x}+1\,\,)^2}$

$F'_4(x)$ est égale à f(x), donc $F_4(x)$ est une primitive de f(x).

Exercice 22 :

a) Une primitive de $5x^4-3x+7$ est : $\frac{5}{5}x^5-\frac{3}{2}x^2+7x+C$ , où C est une constante d’intégration.

b) Une primitive de $4(3x-1)^5$ est : $\frac{4}{18}(3x-1)^6+C$ , où C est une constante d’intégration.

c) Pour trouver une primitive de $\frac{7x}{x^2+4}$ , on fait le changement de variable $u=x^2+4$ .

Alors, on a :

$\int\frac{7x}{x^2+4}dx=\frac{1}{2}\int\frac{7}{u}du=7ln|u|+C=7ln|x^2+4|+C$

d) Une primitive de 3xe^x est : $(3x-3)e^x+C$ , où C est une constante d’intégration.

Exercice 23 :

a) On a 2-2e^t\leq\, 0 pour tout t réel, car $e^t\geq\, 1$ pour $t\geq\, 0$ et donc $e^t-1\geq\, 0$ .

De plus, $2-2e^t=(1-e^t)(1+e^t)\leq\, 0$ car $1-e^t\leq\, 0$ et $1+e^t\geq\, 0$ pour tout t réel.

b) On a $e^{t^2}\geq\, e^t$ pour tout $t\geq\, 1$ , car $t^2>t$ pour tout t>1 et donc $e^{t^2}>e^t$ . Donc :

$2-2e^{t^2}\leq\, 2-2e^t$

c) On a :

$\int_{0}^{1}(2-2e^{t^2})dt\leq\,\int_{0}^{1}(2-2e^t)dt$

$\Rightarrow\,\,\,\int_{0}^{1}(2-2e^{t^2})dt\leq\, 2-2(e-1)$

Mais on a aussi :

$2-2(e-1)\leq\,\int_{0}^{1}(2-2e^{t^2})dt$

$\Rightarrow\,\,\,0\leq\,\int_{0}^{1}(2-2e^{t^2})dt\leq\, ln2$

Donc, on a :

$0\leq\,\int_{0}^{1}\frac{x^n}{1+x}dx\leq\, ln2$

Exercice 24 :

a) On utilise une intégration par parties pour calculer :

$\int_{0}^{1}\frac{x^n}{1+x}dx=[ln(1+x)\times \frac{x^n}{n+1}]_{0}^{1}-\int_{0}^{1}\frac{1}{(1+x)^2}\times \frac{x^n}{n+1}dx$

$=ln2\times \frac{1}{n+1}-\frac{1}{n+1}\int_{0}^{1}\frac{1}{(1+x)^2}\times d(x^{n+1})$

$=ln2\times \frac{1}{n+1}-\frac{1}{n+1}[x^{n+1}\times \frac{-1}{1+x}]_{0}^{1}+\frac{1}{n+1}\int_{0}^{1}\frac{x^{n+2}}{(1+x)^2}dx$

$=ln2\times \frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}\frac{x^{n+2}-x^{n+1}}{(1+x)^2}dx$

$=ln2\times \frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}(\frac{x^{n+2}}{(1+x)^2}-\frac{x^{n+1}}{(1+x)^2})dx$

$=ln2\times \frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}(\frac{x^{n+2}}{1+x}-\frac{x^{n+1}}{1+x})\times \frac{1}{1+x}dx$

$\Rightarrow\,\,\,0\leq\,\int_{0}^{1}\frac{x^n}{1+x}dx\leq\, ln2$

Exercice 25 :

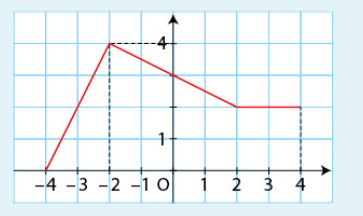
a) Pour calculer $\int_{-4}^{-2}f(t)dt$ , on utilise l’aire sous la courbe entre -4 et -2.

Cette aire est représentée par un rectangle de base 2 et de hauteur 0,5.

Donc :

$\int_{-4}^{-2}f(t)dt=Aire=2\times 0,5=1$

b) Pour calculer $\int_{-2}^{2}f(t)dt$ , on utilise l’aire sous la courbe entre -2 et 2.

Cette aire est représentée par un rectangle de base 4 et de hauteur 1. Donc :

$\int_{-2}^{2}f(t)dt=Aire=4\times 1=4$

c) Pour calculer $\int_{2}^{4}f(t)d$ t, on utilise l’aire sous la courbe entre 2 et 4.

Cette aire est représentée par un rectangle de base 2 et de hauteur -0,5. Donc :

$\int_{2}^{4}f(t)dt=Aire=2\times (-0,5)=-1$

Exercice 26 :

a) $\int_{-2}^{1}5dx=5\times (1-(-2))=15$

b) $\int_{-1}^{2}(-t+4)dt=[-\frac{1}{2}t^2+4t]_{-1}^{2}=(-\frac{1}{2}(2)^2+4(2))-(-\frac{1}{2}(-1)^2+4(-1))=7$

c) $\int_{-3}^{3}(x+3)dx=[\frac{1}{2}x^2+3x]_{-3}^{3}=(\frac{1}{2}(3)^2+3(3))-(\frac{1}{2}(-3)^2+3(-3))=18$

d) $\int_{0}^{5}(2x+1)dx=2\times \frac{5^2}{2}+5=30$

e) $\int_{-2}^{2}(1-\frac{x}{2})dx=[x-\frac{x^2}{4}]_{-2}^{2}=(2-\frac{4}{4})-(-2-\frac{4}{4})=4$

f) $\int_{-1}^{1}(1-|x|)dx=2\int_{0}^{1}(1-x)dx=2[x-\frac{x^2}{2}]_{0}^{1}=2-(0-0)=2$

Exercice 27 :

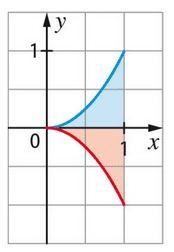
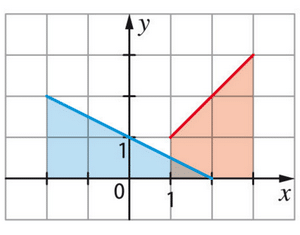
1. L’aire en bleu est délimitée par la courbe de $f(x)=x^2$ entre x=0 et x=1, ainsi que par la droite $y=-x^2$ .

L’intersection entre les deux courbes est lorsque $x=\sqrt{\frac{1}{2}}$ .

L’aire de la surface en bleu est donc la somme de l’intégrale suivante :

$\int_{0}^{\sqrt{\frac{1}{2}}}(x^2-(-x^2))dx=2\int_{0}^{\sqrt{\frac{1}{2}}}x^2dx=\frac{1}{3}$

L’aire en bleu est donc $\frac{1}{3}$ unité d’aire.

2. La surface en rouge est le complémentaire de la surface en bleu par rapport à l’aire délimitée par les courbes de f(x) et g(x).

Comme f(x) est au-dessus de g(x) sur [0;1], la surface en rouge est la somme des aires de f(x) sur $[0;\sqrt{\frac{1}{2}}]$ et de g(x) sur $[\sqrt{\frac{1}{2}};1]$ .

Comme les aires délimitées par f(x) et g(x) sont symétriques par rapport à l’axe des ordonnées, elles ont la même aire.

Donc, l’aire de la surface en rouge est la moitié de l’aire de l’aire délimitée par f(x) sur [0;1], qui est :

$\int_{0}^{1}f(x)dx=\int_{0}^{1}x^2dx=\frac{1}{3}$

L’aire en rouge est donc $\frac{1}{6}$ unité d’aire.

3. La surface en bleu est délimitée par la courbe de $f(x)=x^2$ entre x=0 et x=1, ainsi que par la droite $y=-x^2$ .

Donc, l’aire de la surface en bleu est :

$\int_{0}^{1}(x^2-(-x^2))dx=2\int_{0}^{1}x^2dx=\frac{2}{3}$

On retrouve bien l’aire précédemment calculée.

Exercice 28 :

$I=\int_{1}^{3}xdx=[\frac{1}{2}x^2]_{1}^{3}=\frac{1}{2}(3)^2-\frac{1}{2}(1)^2=\frac{8}{2}=4$

$J=\int_{-2}^{2}-0,5x+1dx=[-\frac{1}{4}x^2+x]_{-2}^{2}=(-\frac{1}{4}(2)^2+2)-(-\frac{1}{4}(-2)^2-2)=-1$

Donc $I \neq J$ . L’affirmation est fausse.

Exercice 29 :

1) Une primitive de $2xe^{x^2-3}$ est $e^{x^2-3}+C$ , où C est une constante d’intégration.

Une primitive de $\frac{x}{x^2+4}$ est $\frac{1}{2}ln(x^2+4)+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $cos(x)sin^2(x)$ , on fait le changement de variable $u=sin(x)$ .

Alors, on a :

$\int cos(x)sin^2(x)dx=-\int u^2du=-\frac{u^3}{3}=-\frac{sin^3(x)}{3}+C$

2) Une primitive de $\frac{2x+1}{x^2+x+1}$ est $ln(x^2+x+1)+C$ , où C est une constante d’intégration.

Une primitive de $\frac{x}{(x^2+1)^2}$ est $-\frac{1}{2}\frac{x}{x^2+1}-\frac{1}{2}arctan(x)+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $x(x^2+5)^{-3}$ , on utilise la substitution $u=x^2+5$ . Alors, on a :

$\int x(x^2+5)^{-3}dx=\frac{1}{2}\int u^{-3/2}du=-u^{-1/2}=-\frac{1}{\sqrt{x^2+5}}+C$

3) Une primitive de $xe^{-x^2}$ est $-\frac{1}{2}e^{-x^2}+C$ , où C est une constante d’intégration.

Une primitive de $\frac{e^x}{e^x+1}$ est $ln(e^x+1)-x+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $\frac{8x}{\sqrt{2x^2+1}}$ , on fait le changement de variable $u=2x^2+1$ .

Alors, on a :

$\int \frac{8x}{\sqrt{2x^2+1}}dx=\int u^{-1/2}du=2\sqrt{2x^2+1}+C$

Exercice 30 :

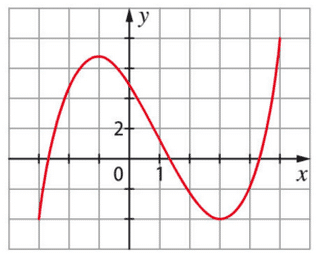
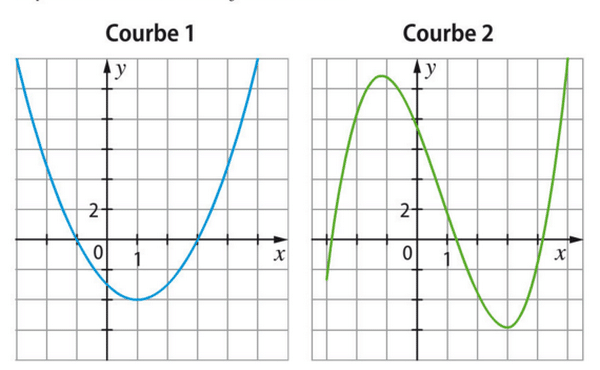
La fonction f est la dérivée de F.

On sait que F est croissante sur [0;2] et décroissante sur [2;5], donc f est positive sur [0;2] et négative sur [2;5].

La première courbe est donc celle de $f(x)$ tandis que la deuxième est celle de $-f(x)$ .

Exercice 31 :

1.a) Pour tout $x\in [n;n+1]$ , on a $n\leq\, x\leq\, n+1$ , donc $\frac{1}{n+1}\leq\,\frac{1}{x}\leq\,\frac{1}{n}$ .

b) Une primitive de $\frac{1}{n}$ est $ln|x|$ , donc :

$\int_{n}^{n+1}\frac{1}{n}dx=ln|n+1|-ln|n|=ln(\frac{n+1}{n})$

c) En utilisant les inégalités de la question a), on a :

$\int_{n}^{n+1}\frac{1}{n+1}dx\leq\,\int_{n}^{n+1}\frac{1}{x}dx\leq\,\int_{n}^{n+1}\frac{1}{n}dx \Rightarrow\,\,\,I_{n}\leq\,\frac{1}{n+1}\leq\, I_{n}$

Donc, on a : $\frac{1}{n+1}\leq\, I_{n}\leq\,\frac{1}{n}$

2) La limite quand n tend vers l’infini de $\frac{1}{n+1}$ est 0 et la limite quand n tend vers l’infini de $\frac{1}{n}$ est aussi 0.

Donc, par le théorème des gendarmes, la limite de la suite $(I_n)$ est 0 également.

4.7/5 - (28816 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calcul intégral : corrigé des exercices de maths en terminale en PDF.» au format PDF.

Ressources de terminale

D'autres cours et exercices à consulter

Arithmétique : corrigé des exercices en terminale spécialité en PDF.

Produit scalaire : corrigé des exercices de maths en terminale en PDF.

Suite numériques : corrigé des exercices de maths en terminale en PDF.

Raisonnement par récurrence : corrigé des exercices de maths en terminale en PDF.

Matrices : corrigé des exercices de maths en terminale en PDF.

Les équations différentielles : corrigé des exercices de maths en terminale en PDF.

Continuité d’une fonction : corrigé des exercices de maths en terminale en PDF.

Barycentre : corrigé des exercices de maths en terminale en PDF.

Exercices de maths interactifs avec saisie au clavier des réponses.

Maths et programmation dans un escape game.

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Calcul intégral : corrigé des exercices de maths en terminale en PDF.

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

D'autres cours et exercices à consulter

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques